| Autor |
Beitrag |
    
Stefan

| | Veröffentlicht am Mittwoch, den 16. Februar, 2000 - 16:59: | 
|
Hallo!
Ich weiß nicht, ob das hier das richtige Forum für mein Problem ist, aber wir behandeln im Moment Integrale und unserer Lehrer gab uns folgende Aufgabe, mit der Aussicht auf einen Einser, wenn man eine richtige Lösung vorlegen kann.
Mit welcher Geschwindigkeit muß man einen Körper von der Erde abschießen, daß er unseren Mond erreicht und mit welcher Geschwindigkeit trifft er auf diesem auf? (unter Berücksichtigung der Erd- und Mondgravitation)
Hoffe ihr könnt mir weiterhelfen.
Gruß
Stefan |
    
Knobelmeister

| | Veröffentlicht am Mittwoch, den 16. Februar, 2000 - 17:28: | 
|
Das ist nicht so einfach...aber ne schöne Aufagbe!
Wieviel Zeit hab ich? Und ist es möglich, Dir die Lösung als eMail zu schicken?
Der Knobelmeister |
    
Stefan

| | Veröffentlicht am Mittwoch, den 16. Februar, 2000 - 17:42: | 
|
Hallole!
Also er meinte bis morgen sollen wir die Aufgabe haben. Das wird vermutlich zu knapp, oder??
Aber vielleicht klappts ja doch. Wäre prima.
meine email addy ist: stke@tecknet.de |
    
Knobelmeister

| | Veröffentlicht am Donnerstag, den 17. Februar, 2000 - 00:21: | 
|
Ne,
tut mir leid, ich hab die passenden Formeln nicht im Kopf, ich müsste schon ne Nacht drüber schlafen!
Gruß,
Der Knobelmeister |
    
Pi*Daumen

| | Veröffentlicht am Donnerstag, den 17. Februar, 2000 - 10:40: | 
|
bald ins physikforum stellen.
http://www.physik4u.de
da sind dann die cracks.
Aber vielleicht erbarmt sich ja noch jemand anderes, diese Aufgabe zu lösen.
Pi*Daumen |
    
Anonym

| | Veröffentlicht am Donnerstag, den 17. Februar, 2000 - 15:29: | 
|
Hilfreich scheint eine Skizze Erde(E), Mond(M) und Verbindungslinie der Mittelpunkte. Messung x ab Erdmitte. Entferung des Mondes a.
Für einen Körper (m, x) zwischen beiden überlagern sich die Gravitationskräfte (allgemein F=-Gamma Mm/r²) der beiden. Wir suchen die Stelle xo, an dem die Gesamtkraft Null beträgt: -Gamma m(E)m/x² = Gamma m(M)m/(a-x)². Ausmultiplizieren liefert eine quadratische Gleichung für xo, abhängig vom Massenverhältnis und Abstand.
Ein von der Erde mit v(E) abgeschossener Körper muß gerade diesen Punkt erreichen, um auf den Mond zu gelangen. (Äquivalent: Vom Gleichgewichtspunkt werden Körper zur Erde bzw. Mond fallen gelassen.)
Zur Anwendung des Energiesatzes ist die Berechnung der potentiellen Energie eines Körpers im Schwerefeld erforderlich E(pot)=INTEGRAL[xo;R(E)] F(x)dx; wie oben F(x)=-Gamma m(E)m/x² + Gamma m(M)m/(a-x)². E(pot)+(m/2)v²=0 ergäbe die gesuchte Geschwindigkeit auf der Erdoberfläche.
[... Abbruch wg .Kopfschmerzen] |
    
H.R.Moser,megamath

| | Veröffentlicht am Sonntag, den 20. Februar, 2000 - 13:22: | 
|
Hi Stefan,
Für einen zusätzlichen Einser wird es Dir nun nicht mehr reichen; die Zeitlimite wird längst überschritten sein. Gleichwohl wollen wir nach einer schulgerechten Lösung Deiner Aufgabe suchen.
Für die Berechnung legen wir zunächst die folgenden Ausgangsdaten zu Grunde:
Masse M1 der Erde: M1 = 5.976* 10^24 kg , Masse des Mondes M2 = 7.35 *10^22 kg ,
Abstand a Erde - Mond : a = 3.844 * 10^8 m.
Mit Hilfe des Gravitationsgesetzes lässt sich auf der Verbindungsstrecke Erdmittelpunkt-
Mondmitttelpunkt der Abstand x* des Erdzentrums vom "Totpunkt" P* berechnen; P* ist derjenige Punkt, in welchem die Anziehungskräfte der Erde bzw. des Mondes auf einen Massenpunkt m entgegengesetzt gleich sind. Wir erhalten die Gleichung:
G* m* M1 / x^ 2 = G* m* M2 / (a - x) ^ 2. Die Gravitationskonstante G und die Masse m heben sich weg , und wir erhalten :
x = x * = a * wurzel (Q) / ( 1 + wurzel (Q )) , wobei Q das Massenverhältnis M1 : M2 darstellt. Die numerischen Werte sind: Q = 81.306 , x* = 0.90017 * a =3.46025*10^8 m
Ferner benötigen wir den Erdradius R1 = 6.367*10^6 m , den Mondradius R2 = 1.7382*10^6 m , die Erdbeschleunigung g = 9.81 m / s^2 , die Mondbeschleunigung g2 = 1.622 m / s^2.
Letztere lässt sich übrigens mit dem Gravitationsgesetz berechnen: m* g2 = G * m * M2 / R2 ^2 , daraus mit G= 6.6732 *10^ - 11 Nm^2 /kg^2 g2 = 6.6732*10^ (-11)*7.35*10^22 / (1.7382^2*10^12).=16.2*10^(-1) m/s^2
Nun kann es erst richtig losgehen und zwar mit dem Energiesatz !
(1) Wir befinden uns auf der Abschussrampe A im Abstand r = R1 vom Erdmittelpunkt.
Für die kinetische Energie benützen wir die Formel E(kin) = ½*m*v^2 , für die potentielle Energie (es handelt sich dabei um Hubarbeit) die Formel
E(pot) = G*m*M1* (1 / R1 - 1 / r (Formel I , Kommentar am Schluss) ;
Es gelten dabei die früher eingeführten Bezeichnungen , r ist der Abstand des Massenpunktes m vom Erdmittelpunkt.
Mit der gesuchten Abschussgeschwindigkeit v1 sieht die Energiebilanz so aus:
In A: r = R1 in P* (Totpunkt) r = x*
E(kin) = ½*v1^2 E(kin ) = 0
E(pot) = 0 E((pot) = G*m*M1* (1 / R1 - 1 / x*)
Summe beider : E1 Summe beider: E2
Energiesatz: Gleichsetzung der Summen: E1 = E2 Dies führt auf die Gleichung für die gesuchte Abschussgeschwindigkeit: ½ * m * v1^2 = 2*G*M1*(1/R1 - 1/x*) , daraus findet man schliesslich v1 = 11073 m /s
Etwas einfacher geht die Rechnung , wenn man nach dem Gravitationsgesetz G*M1 durch g*R1^2 ersetzt.; es kommt dann
v1 ^2 = 2*g*R1^2 * ( 1 / R1 - 1 / x*) = ( Formel II ) 2 * 9.81* 6.367^2*10^12*(1/ (6.367*10^6)-1/(3.46025*10^8)) à v= 11073 m/s
Kommentar: v1 ist etwas kleiner als die sog. parabolische Geschwindigkeit vp = 11190 m/s.
vp wird auch Fluchtgeschwindigkeit oder zweite kosmische Geschwindigkeit genannt; sie wird benötigt , um aus dem Gravitationsfeld der Erde auf einer Parabel zu entfliehen.
(2) Um die Aufprallgeschwindigkeit v2 im Punkt B der Mondoberfläche zu berechnen, können wir analog vorgehen.
Wir ersetzen in der Gleichung (2 ) v1 durch v2 , M1 durch M2 , R1 durch R2 und x* durch y* = a - x* ; wir erhalten die Gleichung
V2 ^2 = 2 * G * M2 * ( 1 / R2 - 1 / y* )
Mit dem Resultat v 2 = 2320 m/s. Diese Geschwindigkeit liegt knapp unter der für den Mond gültigen Fluchtgeschwindigkeit vf = 2380 m/s. was wohl zu erwarten war J .
Anmerkung zur potentiellen Energie und Hubarbeit im Gravitationsfeld der Erde
Um einen Körper der Masse m auf einem (beliebigen ) Weg von P1 nach P2 zu heben, ist die folgende Arbeit W12 = G*m*M1*(1/ r1 -1/ r2) notwendig.
r1 . r2 sind die Abstände der Punkte vom Mittelpunkt der Erde.
Die Formel erhält man durch Integration der Formel des Gravitationsgesetzes.
Int(G*m*M1 / r^2*dr) = - G*m*M1 / r
Die potentielle Energie eines Körpers mit dem Abstand r vom Erdzentrum beträgt somit bezüglich der Erdoberfläche Epot = G *m * M1*(1 / R1 - 1 / r ).
Das muss wohl genügen !
Mit besten Grüssen und Wünschen
H.R. |
    
Anonym

| | Veröffentlicht am Sonntag, den 20. Februar, 2000 - 15:08: | 
|
g1 und g2 sind für die Rechnung zwar nicht erforderlich; wenn man sie aber schon verwendet, dann kann man Gravitationskraft und -potential auch einfacher darstellen: F1=-g1*R1²/x² beziehungsweise V1(x)=g1*R²/x.
Bei der Berechnung des Potentials fehlt leider der Einfluß des Mondes; es handelt sich ja ausdrücklich um ein elementares Zweikörperproblem. Möglicherweise genügt die Lösung als Näherung.
Auf welcher Parabel entfliehen Körper mit der zweiten kosmischen Geschwindigkeit? |
    
Fern

| | Veröffentlicht am Sonntag, den 20. Februar, 2000 - 21:16: | 
|
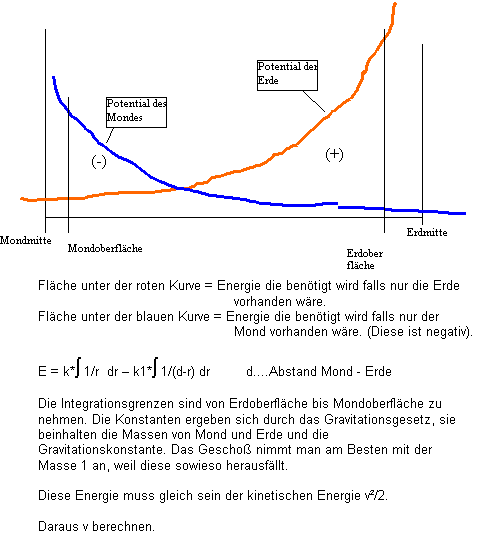
Kurzanleitung zur Berechnung der Abschussgeschwindigkeit:
 |
    
Fern

| | Veröffentlicht am Sonntag, den 20. Februar, 2000 - 21:54: | 
|
Korrektur:
Nun habe ich doch Unsinn geschrieben:
Die obigen Kurven sind natürlich das Gravitationsfeld k/r² und nicht das Potential 1/r.
Unter den Integralen daher auch 1/r² und (d-r)².
Arbeitet man direkt mit den Potentialkurven so erübrigt sich das Integrieren und die Energie ist gleich der Differenz der Potentiale. |
    
Anonym

| | Veröffentlicht am Sonntag, den 20. Februar, 2000 - 22:32: | 
|
Welche Geschwindigkeit willst Du aus der Potentialdifferenz von Erd- und Mondoberfläche eigentlich berechnen? (Ich darf an die Rolle des Totpunktes erinnern.) |
    
Fern

| | Veröffentlicht am Montag, den 21. Februar, 2000 - 10:21: | 
|
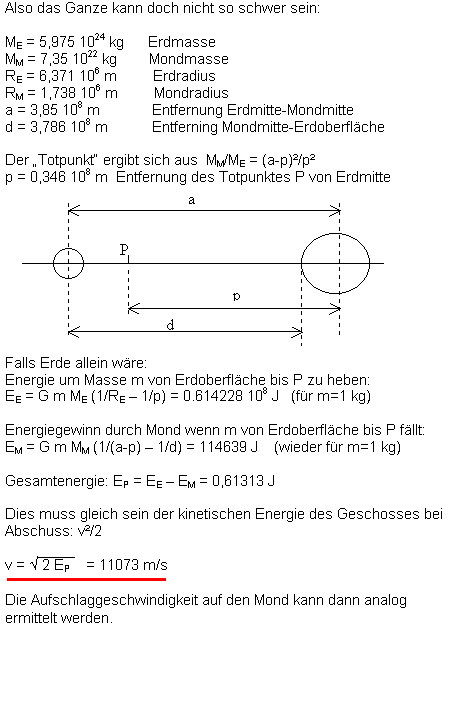 |
    
H.R.Moser,megamath

| | Veröffentlicht am Montag, den 21. Februar, 2000 - 15:08: | 
|
An Anonymus,
Da Du offensichtlich ein Flair für die Himmelsmechanik hast , will ich versuchen, Deine Frage nach den Daten der parabolischen Flugbahn beim Abschuss mit der parabolischen Geschwindigkeit von der Erdoberfläche aus
zu beantworten und Dir zusätzlich einige Delikatessen anzubieten..
Man stösst auf die einschlägigen Formeln , wenn man die Keplerschen Gesetze aus dem Newtonschen Gravitationsgesetz rechnerisch herleitet.
Das geschieht im wesentlichen dadurch, dass man einerseits die allgemeine Kegelschnittgleichung in Polarkoordinaten notiert , wobei man den Pol in einem Brennpunkt wählt (wohin der anziehende Zentralkörper zu liegen kommen wird) und die Polarachse durch den näheren Scheitel legt ( Formel I ) Andrerseits leitet man aus den Bewegungsdifferentialgleichungen, die sich aus dem Gravitationsgesetz ergeben, durch Integration die Schar der Lösungskurven her, die ebenfalls in einem passenden Polarkoordinatensystem dargestellt werden (Formel II).
Durch Vergleich beider Formeln ergeben sich die gewünschten Darstellungen , z.B. für den Parameter p oder die numerische Exzentrizität è des Kegelschnitts.
Die Polargleichung (I) lautet bekanntlich:
1 / r =1 / p + è / p * cos (phi) ,
p: Parameter , é : numerische Exzentrizität , phi Phasenwinkel, r :Radiusvektor
Die Formel (II ), deren Herleitung ziemlich anspruchsvoll ist , lautet -weniger bekanntlich-:
1 / r = L / c^2 + wurzel ( h / c^2 + L^2 / c^4 ) * cos (phi) ,
mit L = G M = g R^2 (G: Gravitationskonstante, M: Masse der Erde,
g: Erdbeschleunigung, R: Erdradius)
c = R * vo (vo :Anfangsgeschwindigkeit , c selbst die
doppelte konstante Flächengeschwindikeit des
Fahrstrahls dar)
h = vo^2 - 2 L / R
Der Vergleich beider Formeln ergibt:
1. p = c^2 / L = R^2 vo^2 / G M = v0 ^2 / g
Spezialfall der Parabel : vo stimmt mit der parabolischen Geschwindigkeit überein; dann gilt vo^2 = 2 g R und der Parameter der Parabel wird
p = 2 R ,und stimmt mit dem Erddurchmesser überein.
2. Numerische Exzentrizität è = p * wurzel ( h / c^2 + L^2 / c^4 ) =
Wurzel ( 1 + c^2 / L^2*h)
Dieser Ausdruck lässt sich sogar umformen zu è = vo ^2 / (g R) - 1
Spezialfall : è = 0 liefert eine Kreisbahn, die zugehörige Geschwindigkeit ist die erste kosmische Geschwindigkeit vo = wurzel (Rg) = 7910 m/s.
Für é zwischen 0 und 1 erscheinen elliptische Bahnen und für è = 1 haben wir wiederum die parabolische Bahn; für diese gilt vo^2 = 2 g R ,woraus man die zweite kosmische Geschwindigkeit errechnen kann.
Ich hoffe, dass ich Deine Frage einigermassen habe beantworten können
.
Mit freundlichen Grüssen
H.R. |
    
Anonym

| | Veröffentlicht am Montag, den 21. Februar, 2000 - 17:13: | 
|
zu Fern: Einige Unebenheiten beiseite: die Korrektur der Integrationsgrenzen (vormals Erde-Mond) führt jetzt zur richtigen Lösung. |
    
Anonym

| | Veröffentlicht am Montag, den 21. Februar, 2000 - 21:23: | 
|
zu megamath: Zur Himmelsmechanik lerne ich gern dazu (wenngleich meine Frage nur darauf zielte, daß bei der beschriebenen linearen Bewegung eine Parabel nicht unmittelbar wahrgenommen wird).
Was berechtigt eigentlich zu der Annahme, daß die Bahnkurven im Zentralfeld einer Punktmasse Kegelschnitte sind? Damit wird das zu beweisende (Keplergesetze) doch teilweise vorausgesetzt. Wäre es nicht besser, die universellen Erhaltungssätzen Energie/Drehimpuls für die Bewegung einer Probemasse in diesem Feld zu spezifizieren?
Was meinst Du mit Anfangsgschwindigkeit? (Wo ist bei einem Kegelschnitt der Anfang?)
Würdest Du freundlicherweise erläutern, wie bei 2./Exzentrizität aus e=p*WURZEL(h/c^2 + L^2/c^4) folgt e=WURZEL(1+c^2/L^2*h) und in der nächsten Zeile e=v0^2/(gR) - 1 ? Und inwiefern folgt daraus für den parabolischen Fall v0^2=2gR? |
    
H,R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 23. Februar, 2000 - 19:42: | 
|
Antwort an Anonymus
1. Erläuterung zur Berechnung der numerischen Exzentrizität è
Pro memoria:
c = R * vo (R: Erdradius, vo: Anfangsgeschwindigkeit)
h = vo ^ 2 - 2 * L / R (L = G * M , G: Gravitationskonstante, M: Erdmasse),
wegen des Gravitationsgesetzes gilt für L auch die Darstellung : L = g * R ^2 , g: Erd-
beschleunigung auf der Erdoberfläche.
è: numerische Exzentrizität der Bahnkurve (Achtung: mit e bezeichnet man
üblicherweise die lineare Exzentrizität)
Wir formen nun é in mehreren Schritten um ( Uebung zur Termumformung) ;
um Quadratwurzeln zu vermeiden, bilden wir è ^ 2:
è ^2 = p^2 * (h / c^2 +L^2 / c^ 4) = c ^4 / L ^2 * ( h / c ^2 + L^2 / c ^ 4) =
1 + c^2 * h / L ^2 = 1 + R^2*vo^2/ (G^2*M^2) * ( vo ^2 - 2*G*M / R) =
(G^2*M^2 + R^2 * vo^4 - 2* R * G * M * vo^2) / ( G^2 * M^2 ) =
(dank einer binomischen Formel) = ( vo^2 *R - G* M) ^2 / ( G^2 * M^2) , somit endlich
(vo^2 * R - G * M ) / (G * M ) = ( vo ^2 * R ) / ( G * M ) - 1 = v o ^2 / g *R - 1
nicht umgekehrt 1- .. wie man sich leicht überlegt
2. Zu Deiner Frage: "Wie folgt daraus für den parabolischen Fall vo ^ 2 = 2 g R ?"
Anwort: Für die Parabel gilt è = 1, somit erhalten wir aus der obigen Darstellung für é :
vo ^ 2 / (g*R) -1 = 1 ,also vo ^2 = 2*g* R..
3. Die Herleitung der Keplerschen Gesetze aus dem Gravitationsgesetz gelingt ohne Zirkel-
schlüsse und stellt für Mechanikvorlesungen zur Dynamik des Massenpunktes u.a. einen
Höhepunkt dar. .Man kann dabei so vorgehen, dass man vorgängig den sog.Flächensatz in einer allgemeinen Form beweist. Dieser Satz enthält als Sonderfall das zweite Keplersche Gesetz und lautet:
Jede Zentralbewegung verläuft in einer das Zentrum enthaltenden Ebene und zwar so , dass der vom Zentrum aus gezogene Fahrstrahl in gleichen Zeiten gleiche Flächen überstreicht.
Bei der Lösung des Differentialgleichungssystems zweiter Ordnung , welche sich aus dem Gravitationsgesetz ergibt ,bietet sich sehr bald das erwähnte Polarkoordinatensystem an, in dessen Pol der Zentralkörper liegt. Die Lösungskurven sind zwingend Kegelschnitte und nichts anderes.
Damit ist eine weitere Frage von Dir beantwortet.
Eine ausführliche rechnerische Herleitung erstreckt sich auf 6 bis 7 Druckseiten A4. Wenn Du Dich dafür interessierst , kannst Du Dich direkt an mich wenden. Wir dürfen
die Fans vom Forum nicht weiter strapazieren , und wir sollten unsere Diskussion im Forum wohl abbrechen.
Mit ganz besonderen Grüssen und bestem Dank für das Interesse !
H.R. |
    
Anonym

| | Veröffentlicht am Donnerstag, den 24. Februar, 2000 - 12:37: | 
|
Deine Term-Notizen zu Punkt 2 scheinen konsistent zu sein (Gleichungen sind es strenggenommen nicht). Man hätte noch an pc^2/L=1 erinnern können.
Zur Herleitung der Keplerschen Gesetze allgemein bin ich anderer Ansicht; aber das könnte man bei Interesse gelegentlich privat weiterspinnen.
Die zwanglose Einführung der Polarkoordinaten ergibt sich übrigens schon auf Schulniveau durch den Drehimpulserhaltungssatz -> ebene Bewegung. |
|





