| Autor |
Beitrag |
    
Andreas

| | Veröffentlicht am Sonntag, den 15. April, 2001 - 20:28: | 
|
Wie kann ich obenstehendes beweisen? |
    
alte ratte

| | Veröffentlicht am Montag, den 16. April, 2001 - 03:40: | 
|
z.b. durch den grenzwert des quotienten
q=ln(x)/x^.5 und zwar durch die h`o´pitalsche regel: 1
lim q für x=>infinity =---------------
x*(1/(2*x^.5))
2*x^.5 2
=lim------- =lim ----- =0
x x^.5
oder,anhand der taylorschen reihenentwicklung, das macht jetzt aber mal ein anderer. |
    
Fern

| | Veröffentlicht am Montag, den 16. April, 2001 - 19:17: | 
|
Hallo Andreas,
Man muss doch zeigen, dass die Ungleichung für alle x > 0 gilt und nicht nur für den Grenzwert x--> oo.
Wir unterscheiden:
0 < x =< 1
Für diesen Bereich ist sqrt(x) positiv und ln(x) nichtpositiv, daher
ln(x) < sqrt(x)
==============
x > 1
Wir formen unsere Ungleichung um:
(ln(x))² < x
Um dies zu beweisen zeigen wir, dass die Steigung der Funktion ln²(x) für jedes x kleiner ist als die Steigung der Funktion x.
Da für x=1 gilt: ln²(x) = 0, kann dann die Funktion ln²(x) nirgends größer angewachsen sein als x.
========================
Ableitungen = Steigung
[ln²(x)]' = 2*ln(x)/x
x' = 1
======
Nun bleibt noch zu zeigen, dass 2*ln(x)/x < 1 ist.
oder gleichwertig: ln(x) < x/2
Dazu siehe Bild:
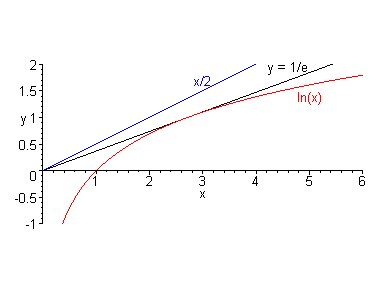
Die Tangente vom Ursprung an die Kurve von ln(x) hat die Steigung 1/e.
(dies kannst du sicher zeigen). ln(x) liegt also unterhalb dieser Tangente.
Die Gerade y=x/2 hat eine größere Steigung, d.h. ln(x) liegt mit Sicherheit auch unterhalb x/2.
=========================
Damit ist gezeigt:
ln²(x) < x
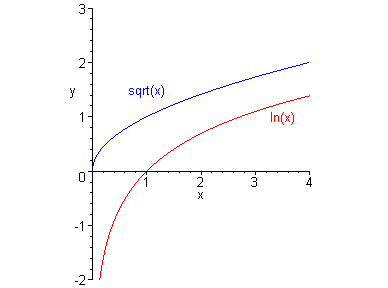
also auch (für x>0) ln(x) < sqrt(x)
===============================
 |
    
lnexp

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 22:04: | 
|
Hallo Andreas
Wesentlich einfacher ist es, die Ungleichung umzustellen:
ln(x)-sqrt(x)<0
Dann definierst Du
f(x)= ln(x) - sqrt(x)
Ableitungen:
f '(x)= 1/x - 1/(2*sqrt(x))
f ''(x)= -1/x^2 + 1/(4*x^1.5)
f '(x)=0 liefert
1/x - 1/(2*sqrt(x))=0 |*2x
2 - sqrt(x)=0
sqrt(x) = 2 |^2
x=4
f ''(4)=-1/16+1/(4*8)=-1/16+1/32<0
Es liegt also ein relatives Maximum vor
Da es die einzige gefundene Extremstelle ist
und f(x) und f '(x) stetig sind, ist das auch ein absolutes Maximum.
f(4)=ln(4) - sqrt(4) = ln(4) - 2<0
Also ist f(x) stets negativ woraus folgt, dass
ln(x) < sqrt(x) gilt für alle x>0. |
    
Frank (Norg)

| | Veröffentlicht am Donnerstag, den 19. April, 2001 - 18:29: | 
|
Hallo.
Ich habe auch noch einen Ansatz:
ln(x) < Öx
ln[(Öx)2] < Öx
2*ln[Öx] < Öx
Substitution: Öx = z
2*ln(z) < z
Den Rest hat Fern schon gemacht.
MfG Frank. |
    
Frank (Norg)

| | Veröffentlicht am Donnerstag, den 19. April, 2001 - 18:37: | 
|
PS.: Ich meine folgendes:
Ist
m*ln(x) < x mit m,x Î Â,
so gilt
m < e.
MfG Frank. |
|