| Autor |
Beitrag |
    
Nadja

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 18:01: | 
|
bräuchte Obersumme zu y = x^2 + 1; zu y = 1/2x^2 + 3 und die herleitung der Obersumme der kubischen Parabel..danke :-) |
    
Peter (analysist)

Erfahrenes Mitglied
Benutzername: analysist
Nummer des Beitrags: 116
Registriert: 04-2002
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 18:54: | 
|
Hallo Nadja,
ich gehe mal davon aus, dass du die Obersumme in einem Intervall [0;a] berechnen willst.
Dazu teilen wir das Intervall, das die Länge a hat, in n gleich große Stücke, von denen dann jedes a/n lang ist.
Denke dir jetzt am jeder Stelle a/n; 2(a/n); 3(a/n) ... bis (n-1)(a/n); n(a/n)=a eine Markierung.
Der Funktionswert an jeder Markierung bestimmt die Höhe des jeweiligen Rechtecks:
Jetzt können wir die Rechteckflächen berechnen (jedes (a/n) lang, Höhe: f(k(a/n)))
1. Rechteck: (a/n)*f(a/n)=(a/n)*[(a/n)^2+1]
2. Rechteck: (a/n)*f(2(a/n))=(a/n)*[4(a/n)^2+1]
3. Rechteck: (a/n)*f(3(a/n))=(a/n)*[9(a/n)^2+1]
...
(n-1). Rechteck: (a/n)*f((n-1)(a/n))=(a/n)*[(n-1)^2(a/n)^2+1]
letztes, n. Rechteck: (a/n)*f(n(a/n))=(a/n)*[n^2(a/n)^2+1]
Alle Flächeninhalte beinhalten den Faktor (a/n), also klammern wir ihn für die Summe aus:
(a/n)[1(a/n)^2+ 4(a/n)^2 + ... +(n-1)^2(a/n)^2+n^2(a/n)^2+ n]
Im letzten "n" habe ich die ganzen Einsen zusammengefasst.
Der Faktor (a/n)^2 taucht in fast allen Summanden auf, erneut ausklammern:
(a/n)[(a/n)^2(1+4+9+...+n^2)+n]
Jetzt ersetzt man noch die Summe der ersten n Quadratzahlen durch (1/6)n(n+1)(2n+1)[lässt sich induktib beweisen]
OS=(a/n)[(a/n)^2(1/6)n(n+1)(2n+1)+n]
=a[(a/n)^2(1/6)(n+1)(2n+1)+1]
=a[(1/6)a^2((n+1)/n)((2n+1)/n)+1]
Jetzt bilden wir den Grenzwert fur n gegen unendlich:
((n+1)/n) strebt gegen 1
((2n+1)/n) strebt gegen 2
=> lim OS=a[(1/6)a^2*1*2+1}=(1/3)a^3+a
....n->OO
Als Beispiel a=3, n=50
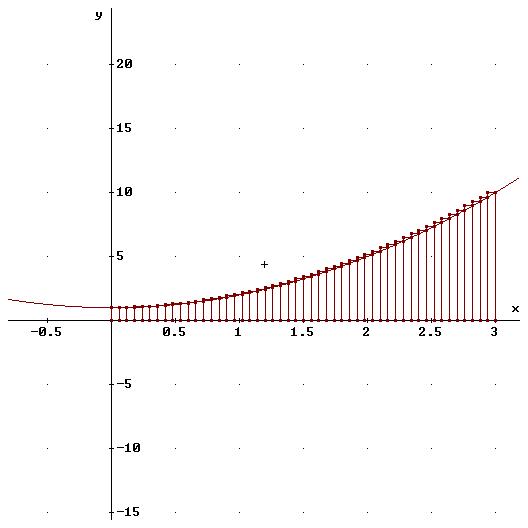
Gruß
Peter |
    
Nadja

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 19:00: | 
|
naja eigentlich von 0 - b ..sorry habe ich vergessen! |
    
mythos2002 (mythos2002)

Fortgeschrittenes Mitglied
Benutzername: mythos2002
Nummer des Beitrags: 79
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 25. September, 2002 - 20:37: | 
|
Hallo Peter,
schön gemacht! Allerdings wurde dieses Thema schon öfter besprochen! Soll man das Rad immer wieder neu erfinden?
sh. z.B. bei
http://www.zahlreich.de/cgi-bin/hausaufgaben/show.cgi?9308/127925
Vielleicht gibt's bei ZahlReich auch so etwas wie FAQ's, dies mal als Anregung für den Moderator!
Gr
mYthos
|
|