| Autor |
Beitrag |
    
Sarah

Unregistrierter Gast
| | Veröffentlicht am Freitag, den 20. September, 2002 - 12:58: | 
|
Hallo ihr! habe ein riesiges problem. bitte helft mir, diese aufgabe zu lösen!
Aus einer rechteckigen Fensterscheibe mit den seitenlängen a und b ist vom Mittelpunkt der kleineren seite aus eine ecke unter einem winkel von 45° abgesprungen. aus der restlichen scheibe soll durch schnitte parallel zu den ursprünglichen seiten eine möglichst große scheibe hergestellt werden. sib die maße der neuen scheibe an!
Ich weiß nicht, wei ich bei dieser aufgabe anfangen soll.
bitte helft mir!!
Sarah |
    
Friedrich Laher (friedrichlaher)

Erfahrenes Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 448
Registriert: 02-2002
| | Veröffentlicht am Samstag, den 21. September, 2002 - 07:52: | 
|
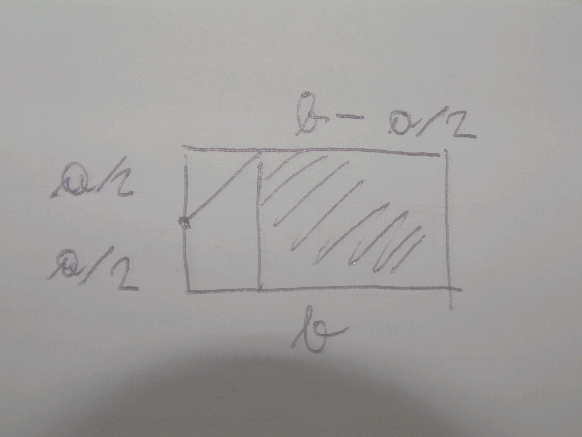
a, b-a/2
(Beitrag nachträglich am 21., September. 2002 von friedrichlaher editiert) |
    
Karl

Unregistrierter Gast
| | Veröffentlicht am Samstag, den 21. September, 2002 - 11:18: | 
|
Hey,
Koordinatensystem aufspannen, x-Achse nach rechts, y-Achse nach oben (von Interesse nur 0<=x<=b, 0<=y<=a). Ich dreh das Bild von oben mal um, d.h. die Ecke sei links unten und die Bruchkante verbindet die Punkte (0,a/2) und (a/2,0), womit sich als Gleichung der Geraden, auf der die Bruchkante liegt, y=-x+a/2 ergibt. Man sucht nun einen Punkt P=(xp,yp) auf dieser Geraden, mit der Nebenbedingung, dass der Punkt auf dem Bruchkantenstück der Geraden liegen soll,
(also yp=-xp+a/2)und zieht von diesem Punkt ausgehend Parallelen zu den Kanten, wodurch sich ein Rechteck ergibt (siehe Skizze oben). Gesucht ist der Punkt P, der für das entstehende Rechteck den maximalen Flächeninhalt A(xp) ergibt.
A(xp)=(b-xp)*(a-yp)=(b-xp)*(a/2+xp)=-xp^2+xp*(b-a/2)+ab/2, A'(xp)=-2*xp+(b-a/2) , A''(xp)=-2
Jetzt A' null setzen, um das Maximum zu finden:
A'(xp)=-2*xpm+(b-a/2)=0 -> xpm=b/2-a/4, A''(b/2-a/4)=-2<0 -> Maximum. ypm=-xpm+a/2=3a/4-b/2, A(xpm)=(b/2+a/4)*(a/4+b/2) (also ein Quadrat)=b^2/4+a^2/16+ab/4. Test: (b>=a/2, sonst könnte man eine solche Ecke nicht abbrechen)-> b>=xpm=b/2-a/4>=0,d.h. der Punkt liegt auf der Bruchkante. Nun noch die Definitionsränder checken: Falls P=P1=(a/2,0) -> A=a*(b-a/2)=ab-a^2/2,
A1-A(xpm)=3ab/4-9a^2/16-b^2/4=-(b/2-3a/4)^2<=0 -> A(xpm)>=A1. Analog am anderen Rand.
D.h. das maximale Rechteck ist ein Quadrat.
Gruß Karl
|
|