| Autor |
Beitrag |
    
Katharina

| | Veröffentlicht am Mittwoch, den 07. Februar, 2001 - 15:22: | 
|
Ich schreibe eine Facharbeit in Mathe, u.a. muß ich folgende Aufgabe lösen:
Bestimmen sie die Tangentenrichtungen im Doppelpunkt der Gleichung r=sin 1/3*phi
Ich habe zuerst die Parameterdarstellung der Gleichung berechnet, also x(phi) und y(phi). davon habe ich dann die Ableitungen gebildet.
Ist das richtig? Ich komme nämlich nicht weiter! |
    
Fern

| | Veröffentlicht am Mittwoch, den 07. Februar, 2001 - 22:26: | 
|
Hallo Katharina,
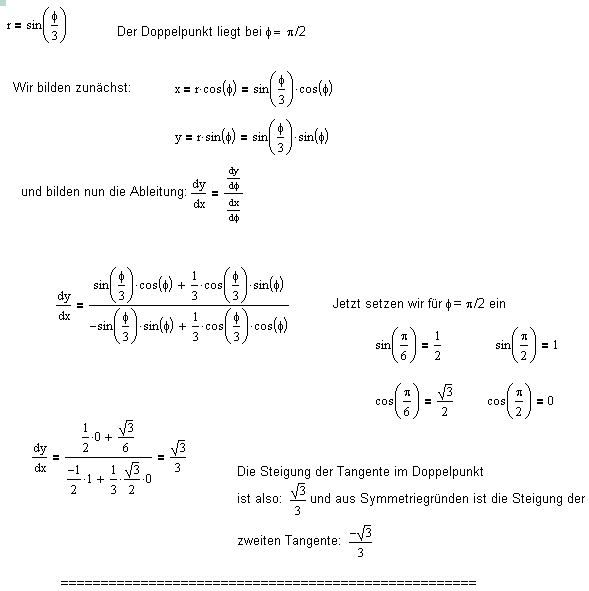
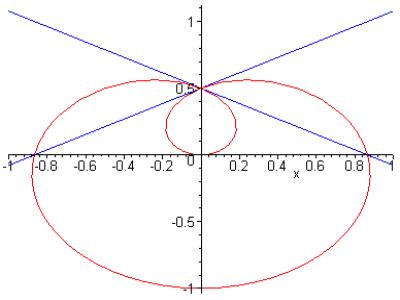 |
    
Katharina

| | Veröffentlicht am Donnerstag, den 08. Februar, 2001 - 13:01: | 
|
Ersteinmal ganz herzlichen Dank für die Hilfe!
Aber eine Frage hätte ich noch: Woher weiß man wo der Doppelpunkt liegt? Kann man ihn auch berechnen oder kann man ihn nur durch betrachten der Kurve benennen? |
    
Fern

| | Veröffentlicht am Donnerstag, den 08. Februar, 2001 - 17:57: | 
|

Aber vielleicht kennt jemand einen einfacheren Weg. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 09. Februar, 2001 - 10:03: | 
|
Hi Katharina,
Ich habe intensiv über Deine Frage bezüglich
eines allfälligen Doppelpunktes der durch eine Polargleichung
gegebenen Kurve meditiert.
Dann stellte Fern eine ausgezeichnete Arbeit darüber ins Board
und beantwortete umfassend auch Deine Zusatzfrage,
sodass das Thema eigentlich erledigt ist.
Trotzdem möchte ich dazu auch noch ein paar KB (Kilobytes)
zum Thema beitragen.
Den Doppelpunkt habe ich mit der folgenden kleinen, nicht sehr
tiefliegenden Rechnung à la laitière gefunden.
Der gesuchte Polarwinkel sei x, daraus wird nach einer vollen
Umdrehung x +360°
Gleiche r-Werte bedingen: sin(x / 3) = sin ( x/3 + 120 ° );
Zu zwei gleichen Sinuswerten gehören u.a. Winkel,
welche sich auf 180° ergänzen , also setzen wir an:
x/3 + x/3 + 120° = 180° , daraus x = 90°, voilà (!)
Die Archimedische Spirale mit der Polarkoordinatendarstellung
r = a * abs (phi) , a konst.>0 ,besitzt mehrere Doppelpunkte ,
die man leicht findet :
es sind - in rechtwinkligen Koordinaten ausgedrückt -
die Punkte D1 (0 / ½ * Pi ) , D2 ( 0 / - 3/2 * Pi ) u.s.w.
Die Suche nach Doppelpunkten wird übersichtlicher, wenn die Kurve
durch eine implizite Gleichung f (x / y) = 0 gegeben ist.
Dann stehen uns handgreifliche Verfahren zur Verfügung,
die ich im folgenden vorführen möchte, zusammen mit
einigen interessanten Beispielen.
Leider lassen sich aber nicht alle Polarkoordinatengleichungen
in die gewünschte Form f(x,y) verwandeln. Tant pis !
Ein wenig Theorie über singuläre Punkte, zu denen die
Doppelpunkte gehören.
Bezeichnungen:
fx: partielle Ableitung von f(x,y) nach x
fy: partielle Ableitung von f(x,y) nach y
fxx, fyy ,fxy sind die entsprechenden zweiten part.Ableitungen
Die singulären Punkte einer Kurve f(x,y) = 0 sind dadurch
gekennzeichnet, dass gleichzeitig die folgenden Gleichungen
gelten:
f(x,y) = 0 , fx = 0 , fy = 0
y ' bestimmt sich aus der Formel
fxx + 2 * y ' * fxy + y ' ^ 2 * fyy = 0 , wir setzen voraus:
fyy nicht null.
d sei die Diskriminante der quadratischen Gleichung für y' :
d = ( fxy ) ^ 2 - fxx * fyy.
Fallunterscheidung
(1) d >0 . Zwei reelle und verschiedene Wert von y'
Doppelpunkt mit zwei verschiedenen Tangenten
(2) d = 0 : Die Kurve hat entweder einen Rückkehrpunkt (Spitze)
oder einen Selbstberührungspunkt.
(3) d<0 : Die Kurve hat im betreffenden Punkt keine Tangente;
der Punkt ist ein Einsiedlerpunkt (isolierter Punkt)
Einig Beispiele in bunter Folge (D:Doppelpunkt mit Tangenten t1,t2)
1.) Blatt des Descartes (folium Cartesii):
x^3 + y^3 - 3 a x y = 0
D(0/0), t1:x-Achse , t2:y-Achse
2.) Lemniskate von Bernoulli:
(x^2 + y^2)^2- 2 a^2 * (x^2 - y^2) = 0
D(0/0), t1: y = x , t2 : y = - x
3) Konchoide(Muschellinie)
x^2 * y^2 - (x-a) ^2 * ( c^2 - x^2) = 0
Für c > a: D(a/0) , für c = a Spitze, für c < a Einsiedler
4) x ^ 4 - 2 a y ^ 3 - 3 a ^ 2 y ^ 2 - 2 a ^ 2 x ^ 2 + a ^ 4 = 0
D1 ( a / 0 ) Steigungen der Tangenten: ( plus,minus ) wurzel(4/3)
D2 (- a / 0 ) Steigungen der Tangenten wie soeben
D3 (0 / - a) Steigungen der Tangenten: ( plus,minus ) wurzel(2/3)
u.s.w.
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
Katharina

| | Veröffentlicht am Samstag, den 10. Februar, 2001 - 10:50: | 
|
Ganz herzlichen Dank für die so umfangreiche Antwort!
Viele Grüße
Katharina |
|