| Autor |
Beitrag |
    
Schrader Ewald

| | Veröffentlicht am Dienstag, den 05. Oktober, 1999 - 09:36: | 
|
Lieber Daniel, Lieber Ingo
Höflichst wollte ich Euren Sachverstand für die Lösung des folgenden Problems bitten:
Ein Schwimmer befindet sich am Punkt A eines kreisförmigen Sees mit 60 m Durchmesser. Er möchte den gegenüberliegenden Punkt B erreichen, er schwimmt aber zu einem anderen Punkt P und geht von dort zu Fuß am Ufer des Sees nach B. Zu welchem Punkt P muß er schwimmen, um in kürzest möglicher Zeit nach B zu kommen, wenn er mit einer Geschwindigkeit von 60 m/min schwimmt und mit 120 m/min geht?
Vielen Dank für Eure Bemühungen im voraus
Ewald |
    
Daniel

| | Veröffentlicht am Dienstag, den 05. Oktober, 1999 - 15:34: | 
|
Hallo Ewald,
hier mein Lösungsvorschlag(, der zum Schluss nicht zum Ergebnis führt):
v1=60m/min
v2=120m/min
r=30m
Man stelle sich einen Kreis im Koordinatensystem vor mit Mittelpunkt M(c=0;d=0) und r=30. Kreisgleichung: r²=(x-c)²+(y-d)²
k: f(x)=wurzel(30²-x²) ;x>-30 und x<30 (Halbkreis)
Um dem jetzt zu folgen, wäre eine Skizze angebracht ...
l1 ist die Länge der Strecke von A(-30;0) bis zu P(a;b)
l2 ist die Länge der Strecke von P(a;b) bis zu B(30;0)
Winkel AMP: cos alpha=(-30+a)/30 ... alpha=arccos(-1+1/30*a)
l1 berechnet sich aus dem Kosinussatz:
l1²=30²+30²-2*30*30*(-1+1/30*a)
l1=wurzel(3600-60a)
l2 berechnet man über das Verhältnis von Nebenwinkel alpha' zu l2 = 180 ° zu halber Kreisumfang:
(180-alpha)/l2=180/(30p)
... l2=(180-alpha)*30p/180
v=s/t ... t=s/v
t(gesamt)=l1/v1+l2/v2
t(a)=wurzel(3600-60a)/60+1/120*(30p-1/6*parccos(1/30*a-1)
t(a) ableiten (vorsicht Kettenregel, ausserdem: d/(dx)(arccos x)=-1/wurzel(1-x²))
t'(a) Null setzen ... a=15 ... hinreichende Bedingung!!!
P(a;f(a))
Blöderweise komme ich hier auf ein Maximum, d.h. er braucht so am längsten. Vielleicht findet jemand meinen Denkfehler und kann ihn korrigieren. (Nach drei Seiten und drei Versuchen mach ich erst mal Pause ... ;-)
Gruss,
Daniel |
    
uli hermann

| | Veröffentlicht am Dienstag, den 05. Oktober, 1999 - 18:00: | 
|
Ich meine, er muss zu Fuß gehen und darf gar nicht schwimmen:
Leider kann ich hier nicht zeichnen, aber ich versuchs mal zu erklären: Nenne den Kreismittelpunkt M und den Punkt wo er wieder aus dem Wasser geht P.
Alpha sei der Winkel BMP.
Dann sieht man (bachte Winkelsummen und gleichschenklige Dreiecke) Winkel BAP = 0.5 mal Alpha und Winkel APB=90° (Thaleskreis).
Er schwimmt die Strecke 2*R*sin(alpha/2) seine Zeit dafür ist: 60*sin(alpha/2) /60 also
tschwimm=sin(alpha/2) Minuten.
Geht er zu Fuß, ist sein Weg alpha*r=alpha*30
Die Zeit zu Fuß ist tfuß=alpha*30/120=alpha/4
wegen alpha<sin(alpha) (Bogenmaß!) kann man abschätzen:
tfuß = alpha/4 < sin(alpha)/4 = 2*sin(alpha/2)*cos(alpha/2)/4
= sin(alpha/2)/2 * cos(alpha/2) =
= tschwimm * cos(alpha/2) < tschwimm weil cos... stets keiner 1 ist. |
    
Ingo

| | Veröffentlicht am Mittwoch, den 06. Oktober, 1999 - 12:15: | 
|
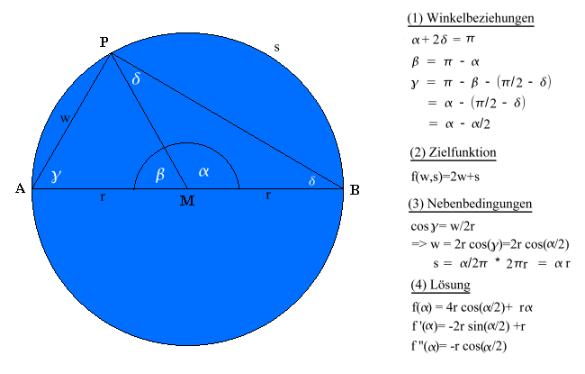
Die Idee von Ulli ist im Prinzip richtig,hat aber leider einen entscheidenden Fehler : Anstelle des sinus muß der cosinus verwendet werden. Ich habe mir mal die Mühe gemacht die fehlende Graphik zu erstellen und mit den nötigen Formeln zu ergänzen. Falls sich daraus Fragen ergeben,einfach nachfragen.
Die Zielfunktion f(w,s) ist allgemein gehalten und gibt nicht die benötigte Zeit an,aber für die Lösung ist nur wichtig,daß der Landweg doppelt so schnell zurückgelegt wird,wie der Wasserweg.
Die genaue Lösung erhält man durch Nullsetzen der 1.Ableitung,wobei a=p/3 sich als Maximum und a=p*5/3 als Minimum herausstellen wird.
 |
    
habac

| | Veröffentlicht am Mittwoch, den 06. Oktober, 1999 - 16:30: | 
|
Zu ergänzen bleibt noch, dass obige Rechnung nur für a <= p = 180o gilt, sonst wird nämlich der cos (a/2) negativ und die Zeit für den Seeweg wird subtrahiert statt addiert.
Diese Extremalaufgabe hat ihr Minimum am Rand und das wäre bei a = p, was schon von Anfang an klar ist, weil die Geschwindigkeit im Wasser nur halb so gross ist wie auf dem nicht doppelt so langen Umweg an Land. Der Schwimmer ist gar kein Schwimmer, sondern ein Läufer.
So long
habac |
    
uli hermann

| | Veröffentlicht am Mittwoch, den 06. Oktober, 1999 - 17:34: | 
|
So entscheidend ist mein Fehler von gestern gar nicht: ich hab mich bloß verlesen und unseren Nichtschwimmer von B nach A befördern wollen und dannstimmt der Sinus schon. Es geht wohl doch ohne Ableitung oder? Interessiert mich inzwischen ja selber. |
    
ingo

| | Veröffentlicht am Mittwoch, den 06. Oktober, 1999 - 22:55: | 
|
Schönes Beispiel wie wichtig auch die Randwerte sein können,denn habac hat recht. |
    
Ewald

| | Veröffentlicht am Donnerstag, den 07. Oktober, 1999 - 15:32: | 
|
Liebe Jungs und (Mädels)
bedanke mich für Euer außerordentliches Interesse - es gibt schon Mathematikaufgaben! Habe mittlerweile seitenweise Blätter voll gemalt und weiter überlegt und möchte Euch folgenden Lösungsvorschlag machen - mit der Frage: ist er korrekt?
v (Geschwindigkeit) = s(Weg)/ t (Zeit)
t = s/v folgt da zwei Wege: t = s1/120 + s2/60
s1 = Kreisbogen s2 = Sekante
Nun alles in Radiant rechnen daraus folgt (180 - Q)=Winkel des Kreissegments; r=30:
t = (rx(180-Q))/120+s2/60=(180-Q)/4 + s2/60=
45-Q/4 + sinQ x 60
(Dies folgt aus der Definition des Sinus - muß dann aber mal 2 genommen werden um auf ganze Sekantenlänge zu kommen)
t`=-1/4+cosQ x 60
Null gesetzt ergibt Q=-1,57 und Q=+1,57
das umgerechnet in Grad nach Pi*Winkel/180 ergibt
89,95 Grad
Herzliche Grüße von Ewald |
    
Anonym

| | Veröffentlicht am Samstag, den 09. Oktober, 1999 - 13:41: | 
|
sieht gut aus. |
    
habac

| | Veröffentlicht am Samstag, den 09. Oktober, 1999 - 14:00: | 
|
Hi Ewald
ich frage mich, wie Du auf 180 - Q kommst, wenn Du alles im Bogenmass (Radiant) rechnest. Sollte es nicht p - Q heissen?
Dann frage ich mich, was Dein Q ist. Ist es wirklich ein Winkel in einem rechtwinkligen Dreieck? Müsste es vielleicht Q/2 heissen?
Ich bleibe bei meiner Meinung, dass das Minimum am Rand ist.
Gruss habac |
    
Daniel

| | Veröffentlicht am Samstag, den 09. Oktober, 1999 - 22:50: | 
|
Hallo Leute,
ich will noch mal meinen Kommentar dazu abgeben. Und zwar habe ich die Gesamtlänge, die der Schwimmer zurücklegt, wenn er bei P(x,y) aussteigt, in folgende Formel gepackt:
l = (wurzel(60x-x²))/(sin(0.5arcsin(1/30*wurzel(60x-x²)))) + 1/6*(pi)*arcsin(1/30*wurzel(60x-x²))
Der erste Summand l_1 ist die Länge der Strecke im Wasser, der zweite Summand die Länge l_2 des Läufers am Seerand. Ich gehe übrigens von einem Kreis aus, der im Koordinatensystem seinen Mittelpunkt bei M(30/0) hat und den Radius 30 besitzt. Für den einfachen Fall x=30 hat sich meine Formel als korrekt herausgestellt.
Wegen t=s/v bei gleichförmig-geradliniger Bewegung ist t_gesamt=l_1/v_1+l_2/v_2 mit v_2=2*v_1. Es entsteht folgende Zeitformel:
t_gesamt(x) = (wurzel(60x-x²))/v_1*(sin(0.5arcsin(1/30*wurzel(60x-x²)))) + 1/(12*v_1)*(pi)*arcsin(1/30*wurzel(60x-x²))
Wenn man nun für v_1 = 60 m/min einsetzen, die Formel ableiten und Null setzen würde, dann käme man auf ein x bei dem der Schwimmer aus dem Wasser steigt, um eine extreme Zeit zu benötigen.
Meine Idee ist folgende: Der Schwimmer muss von A(0/0) über P(x/y) nach B(60/0). Der Kreis hat die Gleichung y²=60x-x². Es gilt
60*cos(alpha) = l_1 (wegen Kosinussatz ... 30²=30²+l_1²-2l_1*30*cos alpha)
l_1=y/sin alpha ... Höhensatz
Gleichsetzen:
y/sin alpha=60*cos alpha
==>wurzel(60x-x²)/sin alpha=60*cos alpha
==>sin (2alpha)=1/30*wurzel(60x-x²) ... denn sin a*sin a=sin 2a
==>alpha=1/2*arcsin(1/30*wurzel(60x-x²))
mit l_1=y/sin alpha komme ich auf den ersten Summanden der o.g. Wegformel
zu l_2:
alpha'=180-alpha
Mit dem Verhältnis von alpha' zu l_2 = 180° zu einem halben Kreisumfang kann ich l_2 berechnen. Das wäre dann der zweite Summand der Formel.
Wo das Minimum nun eigentlich ist, kann ich nicht sagen, weil ich die Funktion garantiert nicht zwei mal ableiten werde.
Gruss, Daniel |
|