| Autor |
Beitrag |
    
Maik

| | Veröffentlicht am Dienstag, den 31. Oktober, 2000 - 13:18: | 
|
Könnte mir jemand die Lösungswegen zu den Aufgaben hier sagen?
(1.) Zeichnen Sie im Intervall (0;2) das
Schaubild von f(x)= 2x^2-x^3.
Die Tangente in einem Punkt P(u/v) des
gezeichneten Parabelbogens schneide die y-
Achse im Punkt S.
Untersuchen Sie die Funktion, die jeder Zahl
zwischen 0 und 2 den zugehörigen y-Wert von
S zuordnet, auf Extremwerte.
Für welchen Punkt P liegt S "am tiefsten"?
(2.) Jede der Funktionen ft(x)= tx^3+(t^2+1)x^2+x
mit t>0 hat eine Wendestelle. Für welchen
Wert t liegt diese Wendestelle am dichtesten
bei Null?
Gebwn Sie den zugehörigen Wendepunkt des
Schaubildes an.
Bitte helft mir! |
    
Andre

| | Veröffentlicht am Dienstag, den 31. Oktober, 2000 - 13:58: | 
|
Nun die Steigung der Tangente von f(x) in
einem Punkt x ist 4x-3x^2.
Nun muss vom Punkt (x;2x^2-x^3) ausgehend,
die Tangente entlangverfolgt werden bis zur
Y-Achse. D.h. die Tangente muss x Einheiten
in negativer Richtung verfolgt werden.
Daher muss vom y Wert x*(4x-3x^2) abgezogen
werden. Damit kommt man zu dem Punkt
(0;2x^2-x^3 - x*(4x-3x^2)) = (0; 2x^3 - 2x^2)
Dieser Punkt nimmt einen Extremalen Y Wert an
fuer 2x^3 - 2x^2 extremal, also 6x^2 - 4x = 0
(Wenn kein Sattelpunkt).
Nun aufloesen : x(6x-4) = 0
Daher sind die Nullstellen x=0 und x=4/6
Einsetzen in die 2. Ableitung (12x-4) bringt
einmal -4 (Maxima) und 4 (Minima)
Also wird fuer x=4/6= 2/3 ein Minima erreicht,
was bedeutet, dass die Tangente im Punkt
(2/3; 2*4/9 - 8/27) = (2/3; 16/27) beruehrt
(Kann mich natuerlich auch verrechnet haben...)
2)
Berechnung der Wendepunkte (Berechnung 2. und
3. Ableitung)
ft'(x)= 3tx^2+2(t^2+1)x+1
ft''(x) = 6tx + 2t^2 + 2
ft'''(x) = 6t
Also, notwendiges Kriterium ist ft''(x)=0,
daher 6tx+2t^2+2 = 0
Nun ist aber die Frage, fuer welches t es ein
kleinstes x gibt. Nun kann man nach x aufloesen
6tx = -2t^2 - 2
x = -t/3 - 1/(3*t)
Dies koennte man als Funktion von t auffassen,
wobei dann x eine Art Y-Wert wird, den es zu
minimieren gilt.
Daher g(t) = -t/3 - 1/3 * t^(-1)
Weiter g'(t) = -1/3 + 1/3 * t^(-2) = -1/3 + 1/(3t^2)
und g''(t) = -2/3 * t^(-3) = -2/(3t^3)
Dann Nullstellen von g'(t) bestimmen :
-1/3 + 1/(3t^2) = 0
1/(3t^2) = 1/3
1 = (1/3)*(3t^2) (da t>0 gefordert!)
t^2 = 1
(t=1) oder (t=-1)
(Da t>0 gefordert) also t=1 Wendestelle
Probe g''(1) = -2/(3*1) = -2/3 OK
Damit liegt fuer t=1 die Wendestelle am naechsten
an Null...
(Da koennte ich mich aber definitiv verrannt haben... ;))
Andre |
    
Harald

| | Veröffentlicht am Dienstag, den 31. Oktober, 2000 - 20:11: | 
|
Hallo Maik,
(1.) Zeichnen Sie im Intervall (0;2) das
Schaubild von f(x)= 2x^2-x^3.
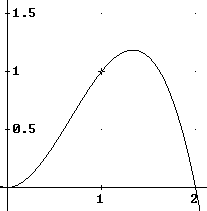 |
    
Harald

| | Veröffentlicht am Dienstag, den 31. Oktober, 2000 - 20:38: | 
|
f(x)= 2x^2-x^3.
Die Tangente in einem Punkt P(u/v) des
gezeichneten Parabelbogens schneide die y-
Achse im Punkt S.
Untersuchen Sie die Funktion, die jeder Zahl
zwischen 0 und 2 den zugehörigen y-Wert von
S zuordnet, auf Extremwerte.
Für welchen Punkt P liegt S "am tiefsten"?
f(x) = -x^3 + 2 x^2
f´(x) = - 3 x^2 + 4 x
Steigung im Punkt P(u | v): x = u !!!
m = - 3 u^2 + 4 u
Da P sowohl auf f, als auch auf t liegt, gilt:
v = f(u) = - u^3 + 2 u^2
t: y = m * x + b
- u^3 + 2 u^2 = (- 3 u^2 + 4 u) * u + b
b = 2 u^3 - 2 u^2
Tangente t:
y = (- 3 u^2 + 4 u) * x + (2 u^3 - 2 u^2)
Für den Schnittpunkt S gilt also:
S( 0 | 2 u^3 - 2 u^2 )
Die Funktion g(u) = 2 u^3 - 2 u^2 ordnet S den y-Wert zu:
g´(u) = 6 u^2 - 4 u
g"(u) = 12 u - 4
Extrema: g´(u) = 0 und Vorzeichenwechsel bzw. 2.Ableitung
6 u^2 - 4 u = 0
6 u ( u - 2/3 ) = 0
u = 0 oder u = 2/3
g"(0) = -4, also Max
g(0) = 0, also Max(0 | 0)
g"(2/3) = +4, also Min
g(2/3) = - 8/27
Für u = 2/3 liegt S am tiefsten: S(0 | - 8/27). |
|