| Autor |
Beitrag |
    
B.Bernd

| | Veröffentlicht am Samstag, den 28. Oktober, 2000 - 01:08: | 
|
Hallo!
Wäre gut, wenn mir jemand sagen könnte, ob die Aussagen weiter unten richtig sind. (eilt nicht)
Ich definiere:
Sei M die Menge der Funktionen m mit folgenden Eigenschaften:
Bei einer Funktion f ÎM liege für eine Stelle x (Î IDf) Monotonie,
aber an der Stelle keine strenge Monotonie, vor.
E sei die Menge der elementaren Funktionen (Anmerkung *, siehe unten)
C sei die Menge der konstanten Funktionen f(x)=c, cÎIR
Sind dann folgende Aussagen richtig?
(A1) für eine Funktion f mit f Î M\C gilt: f Ï E
(A2) für eine Funktion f mit f Î E\C gilt: f Ï M
Anders formuliert:
f sei eine Funktion aus der Menge F, das ist die
Menge aller Funktionen ohne die konstanten Funktionen.
(B1) Wenn f auch nur an einer Stelle nur monoton, aber nicht streng monoton ist, dann ist f nie elementar
(B2) Wenn f elementar ist, ist es nie nur monoton, sondern immer auch
streng monoton (natürlich immer entweder wachsend oder fallend)
Hoffentlich habe ich die B-Aussagen richtig formuliert, so dass B1 mit A1 und B2 mit A2 übereinstimmt.
Anmerkung *) Ich hoffe, dass die Bezeichnung "elementare Funktionen" eindeutig ist, so glaube ich z. B., dass die Betragsfunktion oder die Signumfunktion nicht zu diesen gehören.
Vielen Dank schonmal
Bernd |
    
Zaph (Zaph)

| | Veröffentlicht am Sonntag, den 29. Oktober, 2000 - 13:51: | 
|
Oder zusammenfassend:
Eine elementare Funktion, die an einer Stelle monoton, aber nicht streng monoton ist, ist automatisch konstant.
Bei (B2) hast du "f nicht konstant" vergessen.
Erkläre bitte, was du unter "elementar" verstehst.
Z. |
    
B.Bernd

| | Veröffentlicht am Sonntag, den 29. Oktober, 2000 - 19:38: | 
|
Hallo Zaph,
ich danke dir für die Antwort und auch für die verbesserte Formulierung "Eine elementare Funktion, die an einer Stelle monoton, aber nicht streng monoton ist, ist automatisch konstant. ", auf die bin ich nicht gekommen.
[Was mir jetzt nicht so wichtig scheint, erledige ich gleich zu Anfang:
über den B-Aussagen stand "...Menge F, das ist die Menge aller Funktionen ohne die konstanten Funktionen", so dass bei B1 und B2 von vornherein gelten sollte "f ist nicht konstant";
Oder darf man das nicht so formulieren? - so gut komme ich mit Mengen und Aussagen nämlich nicht klar]
++++++++++++++++++++++++++++++++++++++++++++++++++
Jetzt aber zum Hauptproblem, zum Begriff "elementar":
++++++++++++++++++++++++++++++++++++++++++++++++++
Unter "Elementare Funktionen" steht bei mir zu Beginn von Kapitel 2.5 im Bronstein
Quote:Unter elementaren reellwertigen Funktionen einer reellen Veränderlichen versteht man i. allg. solche, die durch einen analytischen Ausdruck darstellbar sind. Dazu gehören u. a.
die rationalen Funktionen,
die trigonometrischen Funktionen und deren Umkehrfunktionen,
die Exponentialfunktionen, die Logarithmusfunktionen,
die Hyperbelfunktionen und deren Umkehrfunktionen
sowie solche, die sich als Summe, Differenz, Produkt oder Quotient der genannten Funktionen darstellen lassen.
Zu den nichtelementaren Funktionen rechnet man z. B. die Funktion f, die durch
f(x)={0, falls x rational ist; 1, falls x irrational ist
beschrieben wird, desgl. die Funktion y=[x], d. h., y ist gleich der größten ganzen Zahl, die x nicht übersteigt,
...
und die ... Gammafunktion
unter "analytische Funktionen" habe ich dann was in Kap. 3.1.14.6 gefunden, was ich jetzt nicht alles abschreiben will (geschweige denn, einscannen, vgl. deine Antwort auf den Beitrag von gestern, rat mal, wer das war, ich weiß nämlich nicht, ob damit ein Copyright verletzt wird, übrigens, VIELEN DANK nochmals dafür), was sich aber auf die Aussage reduzieren lassen müsste:
Eine (im Punkt x0) analytische Funktion ist als Potenzreihe(nentwicklung um diesen Punkt x0, was für mich eine Taylorreihe bedeutet) darstellbar.
(Ich hoffe, jetzt macht das Resglied bei irgendwelchen logarithm. Funktionen oder sonstwelchen keine Schwierigkeiten mit Konvergenz der Taylorreihe für möglichst viele x0ÎIDf, so langsam verliere ich nämlich vollständig den Überblick, wenn jede Definition eine weitere Schwachstelle nach sich zieht)
Eine Schwachstelle wäre da ja noch das "u. a."
++++++++++++++++++++++++++++++++++++++++++++++++++
Eigentlich müssten ja die Leute, die den Begriff "elementare Funktion" auf den Seiten 25/364, 25/4777, 25/1235 oder 25/4142 benutzt haben, umschreiben können, was das genau ist.
(Hier noch ein Problem zur Angabe einer Seitenadresse von Suchbegriffen bei der Formatierung: Ich habe versucht, einen Link auf diese Linkliste zu kreieren, aber die Adresse der Linkliste heißt nur "http://www.zahlreich.de/cgi-bin/hausaufgaben/board-search.cgi", die richtige Adresse wird, glaube ich, erst angezeigt, wenn man einmal den "<<zurück" oder "weiter>>" -Link aufgerufen hat. Und das kann man erst, wenn es mehr als zehn Seiten zu dem Suchbegriff im Board gibt. Oder gibt es eine einfachere Methode, sich die Seitenadresse der Linkliste anzeigen zu lassen?)
Zum Begriff "elementar" allgemein: wenn es heißt "...nicht elementar lösbar, kann Kai vielleicht was dazu sagen?
Den Begriff "Element" kenne ich zwar aus der Mengenlehre, aber da ich mit der ja nicht so vertraut bin, wie du gemerkt hast, kann ich mir keinen begrifflichen Zusammenhang denken. Vielleicht mit dem Begriff "Element" aus der Chemie ?
Vielen Dank schonmal fürs Lesen |
    
Zaph (Zaph)

| | Veröffentlicht am Sonntag, den 29. Oktober, 2000 - 21:38: | 
|
Hi B.Bernd, liest du den gesamten Bronstein durch ;-)
Also ich finde, dass f(x) = |x| ziemlich elementar ist. "Elementar" hat schon etwas mit Elementen zu tun. In der Chemie sind die Elemente ja gerade die elementaren Bausteine (oder waren es zumindest mal). Duden: "elementar = grundlegend, naturhaft, einfach".
Ein analytischer Ausdruck und eine analytische Funktion ist allerdings etwas verschiedenes, zumindest wenn man von den Definitionen ausgeht, die du hier hin geschrieben hast. Die Gammafunktion lässt sich nämlich sehr wohl in eine Potenzreihe (Taylorreihe) entwickeln.
Was es nun genau heißt, wenn etwas "elementar nicht lösbar" ist, weiß ich leider auch nicht. Und was ein "analytischer Ausdruck" ist und ob |x| einen solchen darstellt, ist mir auch nicht bekannt.
Für eine in eine Potenzreihe entwickelbare Funktion gilt übrigens die Aussage, dass, wenn sie in einem Punkt monoton aber nicht streng monoton ist, konstant sein muss.
Preisfrage an dich: Reicht statt "in eine Potenzreihe entwickelbare" auch "unendlich oft differenzierbare"?
P.S. Das mit der Menge F hatte ich überlesen. |
    
Zaph (Zaph)

| | Veröffentlicht am Montag, den 30. Oktober, 2000 - 18:30: | 
|
Hi B.Bernd,
es ist |x| = Ö(x²). Also ist |x| elementar. Damit ist auch f(x) = x - |x| elementar.Es gilt
f(x) = 0 für x >= 0,
f(x) = 2x für x < 0.
Damit ist f(x) in x = 0 monoton, aber nicht streng monoton. Außerdem ist f(x) nicht konstant.
Gruß Z. |
    
B.Bernd

| | Veröffentlicht am Montag, den 30. Oktober, 2000 - 21:05: | 
|
Hallo Zaph,
vielen Dank für die Beschäftigung mit meiner Frage. Worum es mir eigentlich ging:
Ich wollte mir eine Merkregel für die Eigenschaft "monoton wachsend" aufstellen.
Weil ich einfach nie weiter über den Zusammen hang von f'(x) mit der Def. (x1< x2 => f(x1)£f(x2) usw.) nachgedacht hatte, hielt ich nämlich die Eigenschaft "(nicht streng) monoton" für was ganz anderes, bis Fern mich mal drauf aufmerksam gemacht hat.
Ich muss noch ein bisschen drüber nachdenken, aber ich glaube, mit deinem Satz von 22:38 Uhr
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Für eine in eine Potenzreihe entwickelbare Funktion gilt übrigens die Aussage, dass, wenn sie in einem Punkt monoton aber nicht streng monoton ist, konstant sein muss.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
hast du mir diese hier noch nicht explizit gestellte Frage schon beantwortet.
Das mit der
Preisfrage an dich: Reicht statt "in eine Potenzreihe entwickelbare" auch "unendlich oft differenzierbare"? habe ich, ehrlich gesagt, nicht verstanden. So wie ich eine Potenzreihe verstehe, kommen darin unendlich viele Ableitungen vor.
Könntest du bitte gelegentlich nochmal einen Hinweis (z.B. Link) angeben, wo ich eine Entwicklung der Gammafunktion finde - ist aber nicht dringend -
Im Grunde genommen bin ich mit deinem roten Satz aber schon recht zufriedengestellt und gebe jetzt erst mal Ruhe.
Vielen Dank
Gruß, B. |
    
Zaph (Zaph)

| | Veröffentlicht am Dienstag, den 31. Oktober, 2000 - 16:01: | 
|
Hi B.Bernd,
mit "in eine Potenzreihe entwickelbar" meinte ich, dass die Potenzreihe auch (wenigstens in einem kleinen Intervall und nicht nur am Entwicklungspunkt) konvergiert. Und dazu reicht die Existenz der Ableitungen nicht aus. Das Restglied muss gegen Null gehen!
Eine explizite Darstellung der Potenzreihe der Gammafunktion ist mir nicht bekannt. |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 15:35: | 
|
Hallo Zaph,
gut erklärt, jetzt glaube ich, dass ich verstanden habe: Alle in eine Potenzreihe entwickelbaren Funktionen sind in der Menge der unendlich oft differenzierbaren Funktionen enthalten. Also müsste die Preisfrage mit nein beantwortet werden. Richtig?
Und die Betragsfunktion ist ja wohl nicht in eine Potenzreihe entwickelbar (wahrscheinlich, weil das Restglied eben nicht verschwindet, oder?), so dass der rote Satz (der zwischen den +++++++ -Zeichen) also im Hinblick auf die Betragsfunktion stimmt.
Jetzt möchte ich nur noch gelegentlich wissen, worauf du deine Behauptung
Die Gammafunktion lässt sich nämlich sehr wohl in eine Potenzreihe (Taylorreihe) entwickeln stützt.
Die Reihendarstellung will ich dann gar nicht wissen.
DAnke
Gruß, Bernd |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 16:57: | 
|
Hi B.Bernd, die Preisfrage hast du richtig beantwortet. Aber die Begründung für das "nein" ist falsch. Dass alle in eine Potenzreihe entwickelbaren Funktionen unendlich oft im Entwicklungspunkt differenzierbar sein müssen, ist schon richtig. Gefragt ist jetzt eine unendlich oft differenzierbare Funktion, die monoton, aber nicht streng monoton und nicht konstant ist (und damit nicht in eine Potenzreihe entwickelbar ist).
Die Funktion f(x) aus meinem Beitrag vom 30. Oktober erfüllt das nicht, denn sie ist in x = 0 nicht differenzierbar.
***********************************************
Die Betragsfunktion ist in x = 0 nicht in eine Potenzreihe entwickelbar, da nicht differenzierbar und nicht, da das Restglied nicht gegen Null geht.
***********************************************
Über die Gammafunktion denke ich noch einmal nach. |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 18:05: | 
|
Hallo Zaph,
Danke für die Antwort
Dass die Funktion vom 30.10. in 0 nicht differenzierbar ist, ist klar, aber
begriffsstutzig, wie ich nun mal bin, hat es zwei Möglichkeiten gegeben: entweder, ich überlege mindestens drei Tage und melde mich bis dahin nicht mehr, oder ich frage dich sofort, warum du noch "Gefragt ist jetzt eine unendlich oft differenzierbare Funktion, die monoton, aber nicht streng monoton und nicht konstant ist (und damit nicht in eine Potenzreihe entwickelbar ist)." sagst.
Von meiner Fragestellung "Was für Funktionen sind das, die nicht schwach monoton sind?" bzw. "Wie kann man die Funktionen nennen, die streng monoton sind?" aus müsste doch jetzt alles klar sein.
Die Antwort darauf hast du doch gegeben, (Für eine in eine Potenzreihe entwickelbare Funktion gilt die Aussage: wenn sie in einem Punkt schwach monoton ist, muss sie konstant sein, und die scheint mir richtig zu sein, auch, wenn ich im Moment mehr glaube als nachvollziehe.
Und weil alle in eine Potenzreihe entwickelbaren Funktionen unendlich oft im Entwicklungspunkt differenzierbar sein müssen, ist für meine Frage alles geklärt. Oder nicht?
Synonym: schwach monoton = monoton, aber nicht streng |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 22:03: | 
|
B (am 28. 10. 2:08); Kann ein Tier, das Eier legt ein Zootier sein? Ich hoffe, dass die Bezeichnung "Zootier" eindeutig ist. So glaube ich z. B., dass ein Reptil kein Zootier ist.
Z (am 29.10. 11:51): Anders gefragt: Gibt es Zootiere, die Eier legen? Erkläre bitte, was du unter "Zootier" verstehst.
B (am 29.10. 20:38): Der Grunzschwein definiert "Zootiere" als Tiere, die im Zoo für die Besucher ausgestellt werden. Also z. B. Löwen, Zebras und Elefanten. Die Stubenfliege und der Wolperdinger, so steht dort geschrieben, gehören nicht zu den Zootieren. Außerdem steht im Grunzschwein noch was über Raubkatzen.
Z (am 29.10. 22:38): Liest du den gesamten Grunzschwein durch? :-) Ich hätte im Zoo eigentlich auch Reptilien vermutet. Die Begriffe "Raubkatze" und "Zootier" sind allerdings etwas verschiedenes. Der Wolperdinger ist nämlich sehr wohl eine Raubkatze. Raubkatzen legen übrigens keine Eier. Preisfrage an dich: Gibt es Säugetiere, die Eier legen?
Z (am 30.10. 19:30, triumpfierend): Ich war gestern im Zoo und habe dort auch Krokodile gesehen. Also gibt es Zootiere, die Eier legen.
B (am 30.10. 22:05): Ich glaube mit "Raubkatzen legen keine Eier" hast du meine Frage schon beantwortet. Die Preisfrage an mich habe ich aber, ehrlich gesagt, nicht verstanden. Soviel ich weiß, ist eine Raubkatze ein Säugetier. Und du hast doch schließlich behauptet, dass Raubkatzen keine Eier legen. Und könntest du mir bei Gelegenheit auch erklären, von welcher Raubkatze der Wolperdinger abstammt?
Z (am 31. 10. 17:01): Eine Raubkatze ist ein Säugetier, aber ein Säugetier muss keine Raubkatze sein. Beim Stammbaum des Wolperdingers muss ich leider passen.
B (am 1.11. 16:35): Ich glaube, ich habe verstanden: eine Raubkatze ist ein Säugetier. Also gibt es Säugetiere, die Eier legen. Ach ja, den Stammbaum des Wolperdingers interessiert mich garnicht - ich will bloß wissen, warum das eine Raubkatze ist.
Z (am 1.11. 17:57): Die Antwort auf die Preisfrage ist richtig, aber die Begründung falsch. Gesucht ist ein Säugetier, das Eier legt. Das mit dem Wolperdinger muss ich mir noch einmal in Ruhe überlegen.
B (am 1.11. 19:05 verzweifelnd): Warum fragst du immer noch nach einem eierlegenden Säugetier? Wir waren uns doch einig, dass Raubkatzen keine Eier legen. Oder wie oder was???
Hi B.Bernd. Die Überstzung dieses Dialogs in den unseren überlasse ich dir. Ich hoffe mal, dass ein Schnabeltier Eier legt und zu den Säugetieren gehört. Ansonsten vergiss das mit den eierlegenden Säugetieren. :-) Gruß Z. |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 23:02: | 
|
Hallo Zaph, vielen Dank schonmal hierfür,
du wirst verstehen müssen, dass ich mich jetzt wirklich mindestens drei Tage nicht mehr melde, um das zu übersetzen und für mich widerspruchsfrei nachzuvollziehen, vorab aber schonmal eine Frage:
Eierleger <-> schwach monoton ?
Danke vielmals für die Mühe mit einem Haustier-Halter
Gruß, Bernd |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 01. November, 2000 - 23:14: | 
|
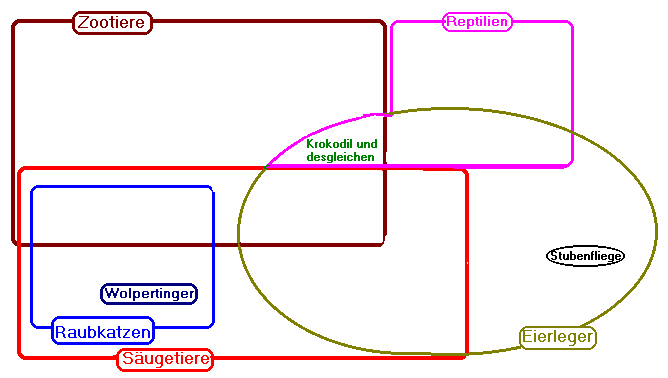
Zootier <-> nichtkonstante elementare Funktion
Reptil <-> Betragsfunktion
Raubkatze <-> analytische Funktion = in Potenzreihe entwickelbar
??? <-> durch analytischen Ausdruck darstellbare F.
Wolpertinger <-> Gammafunktion
Säugetier <-> unendlich oft differenzierbare Funktion
ich glaube, bei meiner Übersetzung für Eierleger fehlt noch eine Einschränkung, aber welche?
Eierleger <-> schwach monoton, nicht konstant ? |
    
Zaph (Zaph)

| | Veröffentlicht am Donnerstag, den 02. November, 2000 - 17:01: | 
|
Hi Bernd, in alten Aufzeichnungen habe ich etwas über die Gamma-Funktion nachgelesen. Ich fürchte aber, dass das nicht sehr befriedigend für dich ist.
Wenn man die Gamma-Funktion als Grenzwert eines Produkts schreibt, wie im Bronstein 2.2.1.1, dann macht es Sinn, das auch für nicht-reelle, nämlich komplexe, Zahlen zu machen. Es stellt sich heraus, das der Grenzwert für alle komlexen Zahlen, außer die nicht-positiven ganzen Zahlen existiert. Das Ergebnis kann aber dann eine komplexe Zahl sein.
Weiterhin macht es Sinn, die Ableitung auch für komplexe Funktionen zu definieren. Und auch hier stellt sich raus, dass die Gamma-Funktion im gesamten Definitionsbereich differenzierbar ist. Man sagt auch, die Gamma-Funktion sei "holomorph".
Für komplexe Funktionen gilt aber im Gegensatz zu reellen Funktionen, dass eine Funktion genau dann in jedem Punkt in eine Potenzreihe entwickelbar ist, wenn sie im gesamten Definitionsbereich differenzierbar ist.
P.S. Zootier = elementar = durch analytischen Ausdruck darstellbar, Reptil = Betragsfunktion, Krokodil = x - |x| (nicht ganz sauber die Analogie), eierlegend = schwach monoton und nicht konstant. Ich hoffe, du hast auch die Moral von der Geschicht' erkannt ;-) |
    
B.Bernd

| | Veröffentlicht am Samstag, den 11. November, 2000 - 20:56: | 
|
 |
    
Zaph (Zaph)

| | Veröffentlicht am Samstag, den 11. November, 2000 - 22:25: | 
|
Wunderwunderschön!!
Aber du hast das Schnabeltier vergessen - darauf kam es mir ja an :-)

Schnabeltier: semiaquatisch lebendes, Eier legendes Säugetier aus Tasmanien und dem Süden und Osten Australiens. (Quelle: Microsoft Encarta 98 Enzyklopädie) |
    
B.Bernd

| | Veröffentlicht am Samstag, den 11. November, 2000 - 23:12: | 
|
Hi Zaph,
Ich war fast jeden Tag im Zoo.
mir kam es erstmal darauf an, dass bis jetzt nix falsch ist. (Ich war mir z.B. gar nicht so sicher, ob es unter den Reptilien bei diesem Vergleich hier überhaupt Eierleger gibt)
Die Eierlegende Wollmilchsau bekommt dann auch noch ihren Platz neben dem Schnabeltier. :-)
Ich gehe jetzt übersetzen.
Gruß, Bernd |
    
B.Bernd

| | Veröffentlicht am Samstag, den 11. November, 2000 - 23:20: | 
|
Korrigiere: ..ob es unter den Eierlegern, die nicht im Zoo zu finden sind, Reptilien gibt
bzw. umgekehrt, ob es unter den Reptilien, die nicht im Zoo sind, Eierleger gibt.
(Völlig unwichtig, aber es fällt grade auf, dass der Zoo keine Vogelabteilung hat) |
    
Zaph (Zaph)

| | Veröffentlicht am Samstag, den 11. November, 2000 - 23:55: | 
|
Soweit ich weiß, legt jedes (weibliche) Reptil Eier, oder ist grundsätzlich in der Lage dazu. Mit Sicherheit gibt es auch Reptilien, die nicht im Zoo gehalten werden. Ja, Vögel gibt es in den mir bekannten Zoos auch. |
    
Jolanta Szewczyk (Jola)

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 12:19: | 
|
Um diese Aufgaben nachfolziehen zu können, bin ich auf jeden Rechnungsschritt angewiesen.
Besten Dank für Eure Hilfe!!!
1 Bestimme Schnittpunkt und Schnittwinkel von f und g mit:
f:x= -4x+2, g:x= -10x+20
Gib eine Funktionsgleichung an für die Höhe hb im Dreieck ABC
A (2/1), B(7/2), C(5/5)
2.Zeichen den Graphen folgender abschnittweise definierten Funktionen:
f:x= -2x-5 für x<=-2
f:x=2/x für -2<x<=-1/3
f:x=x²-4 für -1/3<x<=3
f:x=3/2x-2 für x>3
Zeichen die Graphen folgender Funktionen:
f:x=-2 sin 1/2x
g:x=2hoch(-x+2)
h:x=(x-2)hoch1,5
i:x=-2/3(x-1)(x-3)
3.Bilde die Verkettungen g mit h und h mit g und gib die Definitionsbereiche D g mit h und
D h mit g an.
g:x=2x+3;x Element R h:x=Wurzel aus 1-x²; x Element [-1;1]
g:h=-2/3x+4; x Element R h:x=Wurzel aus x; x Element R+
4.Gib Summe, Differenz, Produkt und Quotient der Funktionen g und h einschl. der Def.menge an und zeichne die Graphen
g:x=1/x; x Element R/0 h:x=x²-2; x Element R
g:x=x²+3x+2; x Element R h:x=x²-x-6; x Element R
5. Bestimme die Umkehrfunktion f und die Definitionsmenge der Umkehrfunktion f
f:x=Wurzel aus x hinter der Wurzel +3; x>=0
f:x=0,5x²-3x-1; D von f ]-unendlich;2]
f:x=2*log2(x+2);x>-2
6. Bestimme den Definitionsbereich so, dass f umkehrbar ist:
f:x=ax²+bx+c
Danke |
    
mori

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 20:27: | 
|
Bei neuer Frage - bitte immer neuen Beitrag öffnen! |
    
Jako

| | Veröffentlicht am Sonntag, den 12. November, 2000 - 20:41: | 
|
Hilfe ich bin verloren;
Ich soll lösen:
ln(3-x)+ln(2)-2*ln(x+1)>=0 |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:07: | 
|
Hallo Jako,
- neue Beiträge werden oft schneller gefunden -
Definitionsbereich der einzelnen Terme:
ln(3-x) für x < 3, 2ln(x+1) für x > -1, also insgesamt -1 < x < 3
ln(3-x) + ln(2) - 2ln(x+1) ³ 0 | +2ln(x+1)
ln(3-x) + ln(2) ³ 2ln(x+1) | Logarithmengesetze ln(a) + ln(b) = ln(a*b) und r*ln(a)=ln(ar)
ln[(3-x)*2] ³ ln[(x+1)2] | exp( )-Funktion auf beide Seiten einwirken lassen
6-2x ³ (x+1)2
x2 + 2x + 1 £ 6-2x |-6+2x
x2 + 4x - 5 £ 0
Entweder löst man diese Ungleichung mit einem kompliziert (vierfach) verzweigten Fallunterscheidungs-Formalismus, oder man begnügt sich mit der anschaulichen Frage, wo der Graph der Parabelfunktion
g(x) = x2 + 4x - 5 nicht oberhalb der x-Achse verläuft, dies ist genau im Intervall, das durch die Nullstellen von g(x) begrenzt wird (Nullstellen mit p-q-Lösungsformel für quadratische Gleichungen), also
-5 £ x £ 1, der Fall.
Zusammen mit dem Intervall, auf dem die Funktion definiert war, ergibt das den Bereich
-1 < x £ 1
========
Durch künstliche Veränderung an der gegebenen Ungleichung (ln(3-x) + ln(2) - ln[(x+1)2] ³ 0 )könnte man den Definitionsbereich für negative x ausdehnen auf x < 3, also auf das Intervall ]-¥;3[, ob das allerdings erlaubt ist, weiß ich nicht. In der Anwendung dieser Ungleichung auf eine Problemstellung wüsste man, ob das sinnvoll wäre.
Dann ergäbe sich eine Lösungsmenge von
-5 £ x £ 1
=======
kleiner Test mit einem Bildchen des Graphen von f(x) = ln(3-x) + ln(2) - 2ln(x+1)

Hallo Jolanta, in der Hoffnung, dass du dich nicht wieder über drei Monate lang nicht zurückmelden wirst, so wie seit dem 11. August, als Georg dir auf Seite http://www.mathehotline.de/mathe4u/hausaufgaben/messages/25/4344.html die Lösungen aufgeschrieben hat, schreibe ich noch ein paar auf Seite http://www.mathehotline.de/mathe4u/hausaufgaben/messages/25/7113.html |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:11: | 
|
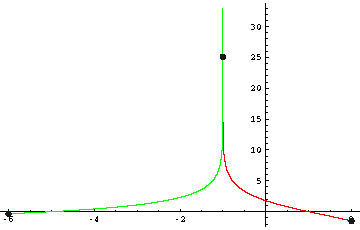
Bild, rot die Funktion f(x) = ln(3-x) + ln(2) - 2ln(x+1) , grün die Funktion ln(3-x)+ln(2)-ln(x+1)²
 |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:12: | 
|
rot die Funktion f(x) = ln(3-x) + ln(2) - 2ln(x+1)
grün: dieselbe Funktion, erweitert unter x£1: ln(3-x)+ln(2)-ln(x+1)²
 |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:13: | 
|
Bild, rot die Funktion f(x) = ln(3-x) + ln(2) - 2ln(x+1)
grün: dieselbe Funktion, erweitert unter x£1: ln(3-x)+ln(2)-ln(x+1)²
 |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:15: | 
|
 |
    
bb

| | Veröffentlicht am Montag, den 13. November, 2000 - 05:41: | 
|
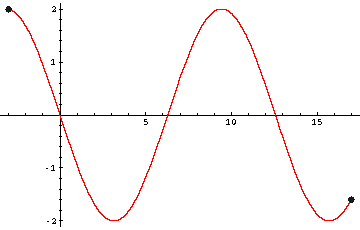
f(x) = -2*sin((1/2)x)
 |
    
B.Bernd

| | Veröffentlicht am Montag, den 13. November, 2000 - 06:18: | 
|
falsche Seite erwischt |
|