| Autor |
Beitrag |
    
Sandra (Fireball)

| | Veröffentlicht am Freitag, den 29. September, 2000 - 15:18: | 
|
Hallo ihr alle!
Ich hoffe, das ist die rcihtige Rubrik für mein Thema. Ich brauche dringend Hilfe zu Funktionenscharen.Meine Frage :
Für k Element R ist f(x)=-xhoch3+k*xhoch2+(k-1)*x
Zeige, dass sich alle Funktionsgraphen in genau zwei Punkten schneiden!
Wer weiß die Antwort und kann mir den Rechenweg genau erklären? Wie kann ich mir das graphisch vorstellen?
Bitte schreibt mir, es wird benotet!
Danke schon mal!
Ciao, Sandra |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 29. September, 2000 - 20:53: | 
|
Hi Sandra
Um Dir zu helfen, es graphisch vorzustellen, folgendes Bild:

Die verschiedenen Farben stellen den Graphen bzgl. verschiedener Koordinaten dar.
An diesem Schaubild sieht man schon, dass es die Punkte 0 und -1 sein muessen, jetzt gehen wir mal analytisch vor:
Wir suchen also die Stellen, fuer die fk(x)=fl(x) gilt, unanbhaengig von den Parametern k und l. Bei der Loesung von Gleichungssystemen empfielt es sich eigentlich immer, nach nullstellen zu suchen, da man dann durch Faktorisieren leicht ans Ziel kommt. Unsere Ausgangsgleichung ist aequivalent zu:
fk(x)-fl(x)=0
Einsetzen des Funktionsterms ergibt:
-x³+kx²+(k-1)x-(x³+lx²+(l-1)x)=-x³+x³+kx²-lx²+(k-1)x-(l-1)x=(k-l)x²+(k-l)x=(k-l)(x²+x)=(k-l)x(x+1)
Da Term ja unabhaengig von den Parametern sein soll, beachten wir den Faktor (k-l) gar nicht. Aber man sieht, dass unabhaegig von k und l an der Stelle x=0 und x=-1 der Term immer 0 ist, daher dort die Funktionen zu allen Parametern den Gleichen funktionswert haben.
viele Gruesse
SpockGeiger |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 29. September, 2000 - 20:57: | 
|
Hi Sandra
Nachtraeglich noch das Bild, wollte erst nicht:
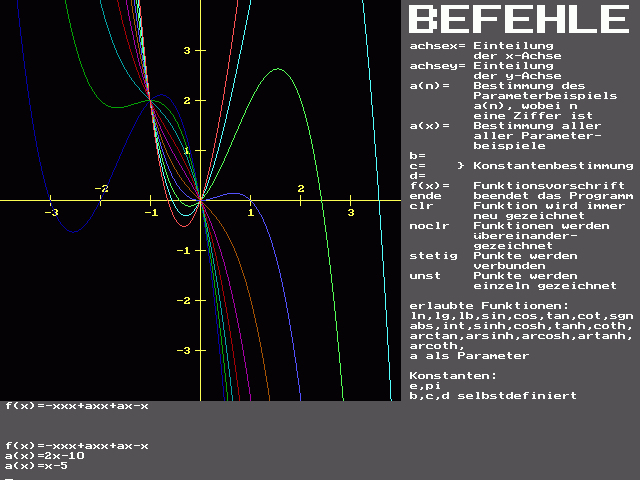
viele Gruesse
SpockGeiger |
    
Sandra (Fireball)

| | Veröffentlicht am Samstag, den 30. September, 2000 - 10:14: | 
|
Hallo SpockGeiger,
danke für deine Antwort und den tollen Graph! Eine Sache verstehe ich nur noch nicht : Wie kommst du auf fk(x)=fl(x)? den Rest hab ich verstanden.
Bye,Sandra. |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Samstag, den 30. September, 2000 - 11:21: | 
|
Hi Sandra
Du suchst doch Punkte, die immer gleich sind, mit anderen Worten suchst Du Stellen, an denen die Funktion, egal bei welchem Parameter, immer den gleichen Funktionswert hat. Also nehme ich mir einfach zwei Funktionen daher, mit irgendwelchen Parametern, und nenne die einfach k und l. Hab das Gefuehl, als waere das nicht sehr erleuchtend, ich versuche es noch etwas anschaulicher:
Die Schar, die ich als Bild geschickt hatte, hat als Parameter ganze Zahlen zwischen -5 und 4. An dem Graphen sieht man, dass z.B. f2 und f-5 in x=0 und x=-1 den gleichen Funktionswert haben, auch f1 und f0, oder f-3 und f{4} usw. Also alle Paare von Fuktionen haben in diesen zwei Punkten den gleichen Wert, daher haben sie auch alle zusammen an diesen Stellen den gleichen Wert (weil Gleichheit eine Aequivalenzrelation ist, falls Dir das was sagt, wenn nicht, dann ueberlies das einfach)
Jetzt verallgemeinern wir das aber nicht nur fuer diese 10 fuktionen, sondern fuer alle. Das sind aber unendlich viele, die koennen wir nicht alle durchrechnen, daher nehmen wir einfach zwei beliebige Parameter k und l. Durch Aequivalenzumformungen sind wir dann zu einer Gleichung gelangt, die fuer x=0 und x=-1 immer erfuellt ist, egal wie k und l aussehen. Lesen wir dann die Umformungen rueckwaerts, dann folgt aus x=0 oder x=-1 eben fk(x)=fl, und zwar fuer alle Parameter k und l, also sind alle Funktionen an diesen Stellen gleich.
So eine Aufgabe gibt es nicht haeufig, deshalb ist mir gerade aufgefallen, dass ich eine andere Moeglichkeit voellig ausgelassen habe. Man koennte auch ein festen Parameter auswaehlen, dafuer den Funktionsterm berechnen, dabei bieten sich immer die Parameter an, die den Funktionsterm vereinfach. In diesem Fall waeren das k=0 oder k=1 (denn dann faellt ein Summand weg). Diesen Term vergleicht man dann mit dem Funktionsterm zu einem beliebigen Parameter vergleichen. Daraus wuerde auch folgen, dass alle Funktionen an diesen Stellen gleich sind.
Ich weiss nicht, ob das verstaendlich war, wenn nicht, dann ueberleg Dir mal, wie Du die Ausgangsgleichung interpretierst. Vielleicht kommen wir dann weiter.
Das rechne ich auch noch mal vor, damit das Prinzip klarer wird (fuer k=0)
f0=fm (m ist irgendein Parameter, Lehrer sagen oft dazu "beliebig, aber fest")
-x³-x=-x³+kx²+(k-1)x
0=kx²+kx=kx(x+1), wie erwartet , kommt dabei dasselbe raus.
Wenn Du meine "Ansprache" verdaut hast, versuch es mal fuer k=1 oder irgendein anderes k (beschraenkt Dich dabei aber auf ganze Zahlen, ich koennte mir keine schlimmere Folter vorstellen, als das fuer z.B. wurzel(5)-ln2 durchzurechnen)
viele Gruesse
SpockGeiger |
    
Sandra (Fireball)

| | Veröffentlicht am Samstag, den 30. September, 2000 - 11:48: | 
|
Hey du!
Super, ich glaub das ist die erste Aufgabe in mathe die ich dieses Schuljahr dank deiner Hilfe verstanden habe! Vielleicht könntest du mir noch bei etwas anderem helfen :
Für die selbe Funktionenschar sollen wir den Wert des Parameters herausfinden an der der graph keinen Extrempunkt/ Wendepunkt hat.
Ich habe dafür die 1. bzw. zweite Ableitung ungleich null gesetzt.Aber wenn ich
-3*hoch2+2kx+(k-1) habe ist es doch egal, welchen Wert ich für k einsetze, weil solange x ungleich null ist die Gleichung immer ungleich null ist. Stimmt das ? Wenn ja wie kann ich das zeigen/beweisen? Bei den Wendestellen wäre das doch der selbe fall, oder?
Danke für deine Antwort,
Bis bald, Sandra |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Samstag, den 30. September, 2000 - 15:45: | 
|
Hi Sandra
Das hab ich nun davon, es geht gleich weiter mit Frage. Nein, war nur n Scherz, ich freue mich sehr, dass es verstaendlich war.
Bei der naechsten Aufgabe begehst Du einen Denkfehler. So, wie Du argumentierst, beweist Du, dass es zu jedem Parameter einen Punkt gibt, sodass die erste Ableitung ungleich 0 ist. Was aber bewiesen werden muss, ist, ein k zu finden, sodass die erste Ableitung keine Nullstellen hat.
Versuchen wir es mal:
f'(x)-3x²+2kx+k-1=0
Wir loesen einfach die Gleichung nach x auf, achten aber nicht wirklich auf das Ergebnis, sondern schauen nur, bei welchen k es ueberhaupt Ergebnis(se) gibt.
x²-2/3*kx-(k-1)/3=0
Jetzt bin ich etwas faul, und betrachte die Diskriminate, das reicht ja aus.
D=(p/2)²-q in der pq-Formel, dass ist hier:
k²/9+(k-1)/3 < 0
k²+3k-3 < 0
Mensch, hast Du DIr die Aufgabe ausgedacht, oder hab ich mich verrechnet???
k²+3k+2,25 < 5,25
w heisst Wurzel
Das gilt fuer -3/2-1/2*w(21) < k < -3/2 +1/2*w(21)
f''(x)=-6x+2k
Ich wuerde sagen, die Aufgaben waren getrennt zu betrachten, denn dieser Term hat immer eine Nullstelle.
Also:
keine Extrema gibt es unter der oben genannten Bedingung, Wendestellen gibt es immer.
viele Gruesse
SpockGeiger |
    
Sandra (Fireball)

| | Veröffentlicht am Montag, den 02. Oktober, 2000 - 09:39: | 
|
Hey du!
Danke erstmal, das du dir Mühe gibst einem hoffnungslosen Fall wie mir zu helfen.
Ich hab noch ein paar Fragen zu deinem letzten Eintrag :
1) Warum reicht es in diesem Fall aus die Diskriminante auszurechnen, anstatt die ganze PQ-Formel anzuwenden?
2)wie kommst du von k²+3k-3<0 auf
k²+3k+2,25<5,25 ?
Und von da aus dann auf die nächste Zeile?
Wieso z.B. w(21) ?
Bis bald, Sandra |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 06. Oktober, 2000 - 12:55: | 
|
Hi Sandra
Tschuldige, dass ich Deine Frage nicht gesehen habe, Deine Idee mit der ansprechenden ueberschrift hat jedoch gewirkt. Muss sagen, ich fuehle mich geschmeichelt. Nun aber zu der Aufgabe:
1)Die Diskriminante ist in der pq-Formel das, was unter der Wurzel steht. Wenn sie negativ ist, gibt es die Wurzel davon nicht, sprich, es gibt keine Loesungen, daher kann man die pq-Formel gar nicht weiterrechnen.
2) Ich hab 5,25 addiert. Warum? Quadratische Ergaenzung. Sei p der Koeffizient von k, dann brauche ich als letzten (konstanten) Term (p/2)2, in dem Fall also (3/2)^2, und dass ist gerade 2,25 oder 9/4, da aber schon eine -3 dasteht, muss ich insgesamt 5,25 dazuaddieren, damit das da steht, was ich haben moechte.
Den Rest hab ich faulerweise mit Maple gerechnet, aber es geht auch per Hand:
k^2+3k+2,25 < 5,25
Das ganze in Bruechen schreiben, mit den laesst es sich besser rechnen:
k^2+3k+(2 1/4) < 5 1/4
k^2+2*3/2*k+9/4 < 21/4
k^2+2*3/2*k+(3/2)^2 < 21/4
Auf der linken Seite steht ein Binom, das koennen wir zusammenfassen:
(k+3/2)^2 < 21/4
Beim Wurzelziehen in Ungleichungen dreht sich das Vorzeichen bei der negativen Loesung um:
-w(21/4) < k+3/2 < w(21/4)
-w(21)/w(4) < k+3/2 < w(21)/w(4)
im letzten Schritt hab ich die Multiplikativitaet der Wurzel ausgenutzt, und w(4) koennen wir auch ausrechnen. w(21) laesst sich jedoch nicht wesentlich vereinfachen:
-w(21)/2 < k+3/2 < w(21)/2
-w(21)/2-3/2 < k < w(21)/2
viele Gruesse
SpockGeiger |
|