| Autor |
Beitrag |
    
Cosine (Cosine)

| | Veröffentlicht am Dienstag, den 08. August, 2000 - 17:44: | 
|
Hi an alle, die da sind!
Mal wieder eine nichtdringende Frage, bei der ich aufgegeben habe, nachdem ich ewig darüber nachgedacht habe. Nagut ich habe nie sehr lange am Stück darüber nachgedacht, aber immer mal wieder ein bisschen...
Frage:
Kovergiert oder divergiert folgende Reihe?
S¥ n=1( nÖ(n) -1 )
Ich habe es mit einigen Konvergens-Tests versucht, von denen mir leider nur die englischen Namen bekannt sind. (Test for Divergence, Simple Comparison Test, Limit Comparison Test, Ratio Test, Root Test), aber das wollte irgendwie alles nicht hinhauen...
Also falls irgendjemand die Lösung kennt,...
Ciao
Cosine |
    
Zaph (Zaph)

| | Veröffentlicht am Dienstag, den 08. August, 2000 - 20:57: | 
|
Hi Cosine, ein paar Vokabeln:
Ratio Test = Quotientenkriterium,
Root Test = Wurzelkriterium.
Dein Problem löst man mit dem "Majorantenkriterium" (= simple comparison test??). Die Reihe ist jedenfalls divergent. Meiner Erfahrung nach ist allein das Wissen, das es eine Lösung für ein Problem gibt, enorm hilfreich, um auf die Lösung zu kommen. Falls du hängst, gebe ich aber gerne weitere Tipps ... Z;-) |
    
Cosine (Cosine)

| | Veröffentlicht am Dienstag, den 08. August, 2000 - 21:59: | 
|
Simple Comparison Test ging ungefähr so:
Wenn für alle n > irgendeinem Startwert N gilt, dass:
0£an£bn
, dann folgt aus
I.) S an div. => S bn div.
und
II.) S bn conv. => S an conv.
oder so in der Art...
Und Du meinst, mit dem käme ich hier weiter???
Das hieße ja, dass ich eine Reihe brauche, die immer kleiner ist als (nteWurzel(n)-1), von der man einfach sagen kann, dass sie divergiert...
Hmmm...
Ich denke mal drüber nach.
Danke erstmal, Zaph
Ciao
Cosine |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 09. August, 2000 - 16:36: | 
|
Was du beschreibst, ist exakt das Majorantenkriterium. Ja, damit kommst du weiter. Sooo viele divergente Reihen, deren Folgeglieder gegen 0 konvergieren, kennst du wahrscheinlich nicht. Versuch's mal mit der, die dir als erstes einfällt... |
    
Cosine (Cosine)

| | Veröffentlicht am Mittwoch, den 09. August, 2000 - 18:41: | 
|
Danke Zaph!
Ich hab's mit der harmonischen Reihe versucht, und ich bin dann auf Umwegen auch drauf gekommen. Es fehlt mir jetzt noch ein schön kurzer Rechenweg, warum nteWurzel(n)-1 > 1/n ist. Mein Weg scheint zwar zu funktionieren, kommt mir aber noch zu lang vor...
Bis jetzt sieht es so aus:
Ich habe angefangen mit der Ungleichung
nÖ(n)-1 £ 1/n
Angenommen es gibt n-Werte, die diese Ungleichung erfüllen, dann muss für diese n-Werte gelten, dass:
nÖ(n) £ 1+1/n
=> n £ (1+1/n)n
Auf der rechten Seite haben wir nun die Eulersche Folge, die immer kleiner als e ist, also ergibt sich:
n £ (1+1/n)n < e
=> Die Ungleichung nÖ(n)-1 £ 1/n kann also nur wahr sein für n=1 und n=2.
Für n ³3 muss also dann gelten, dass
nÖ(n)-1 > 1/n
Und da S 1/n divergiert, divergiert S nÖ(n)-1 ebenfalls (nach dem Majorantenkriterium)
q.e.d.
Allerdings hätte ich das ganze gerne ohne e hingekriegt...
Aber ohne Deine letzte Nachricht wäre ich wohl nie auf die Idee gekommen, es mit 1/n zu probieren. Ich hatte nur an kompliziertere Reihen gedacht...
Ciao
Cosine |
    
Cosine (Cosine)

| | Veröffentlicht am Mittwoch, den 09. August, 2000 - 18:54: | 
|
Andere Frage, Zaph, wo wir gerade bei Reihen sind:
Gibt es eine Möglichkeit, wie man
S¥ n=11/n² berechnet?
(ich kann nur zeigen, dass es konvergiert, und in meinem Calculus-Buch steht auch nur, dass es schwer ist, den Grenzwert zu berechnen...)
Ich habe mal versucht, von der geometrischen Reihe
S¥ n=1xn-1 = 1/(1-x)
auszugehen, dann zu integrieren:
S¥ n=1xn/n = -ln(1-x)+C,
(wenn man für x=0 einsetzt, ergibt sich C=0)
S¥ n=1xn/n = -ln(1-x),
dann durch x:
S¥ n=1xn-1/n = -ln(1-x)/x,
und nochmal integrieren:
S¥ n=1xn/n² = (???)
Auf der linken Seite des Gleichung hätte ich nun die gesuchte Reihe, wenn man für x = 1 einsetzt, aber die rechte Seite will irgendwie nicht...
War aber 'n Versuch wert...
Ciao
Cosine |
    
Susi

| | Veröffentlicht am Mittwoch, den 09. August, 2000 - 19:52: | 
|
Hi Cosine,
Ich habe in einem Buch die gleiche Bemerkung gefunden:
Der Beweis für S¥ n=1=1/n² sei äußerst schwer zu finden.
Er wurde erstmals von Leonhard Euler geführt.
Resultat: S¥ n=1= p²/6 = 1,645...
Aber Zaph kann uns es vielleicht zeigen. |
    
Susi

| | Veröffentlicht am Mittwoch, den 09. August, 2000 - 19:55: | 
|
Formatierungsschwierigkeiten: es muß natürlich immer:
S¥ n=11/n² heißen. |
    
Zaph (Zaph)

| | Veröffentlicht am Donnerstag, den 10. August, 2000 - 19:42: | 
|
Zaph kennt leider auch keinen einfach(er)en Beweis. Weder dass n-te Wurzel n minus eins größer eins durch n noch dass Summe eins durch n Quadrat gleich Pi Quadrat sechtel. |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Donnerstag, den 10. August, 2000 - 21:05: | 
|
Hallo
Den Bewis fuer Summe 1/n² hatten wir als Uebungsaufgabe, wenn es jemanden interessiert, werde ich mir die Arbeit machen, waerte aber cool, wenn ich es als Starofficce-File schicken koennte, ist am einfachsten, bis demnaechst, ich such's mal raus
SpockGeiger |
    
Cosine (Cosine)

| | Veröffentlicht am Donnerstag, den 10. August, 2000 - 21:20: | 
|
Hi Spockgeier!
Das wäre sehr nett von Dir.
Hast Du eine Ahnung, ob man Staroffice-Dateien mit Microsoft Word öffnen kann?
Aber interessiert wäre ich auf jeden Fall.
Ciao
Cosine |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Donnerstag, den 10. August, 2000 - 22:24: | 
|
Hi Cosine
Ich habe mir diese Aufgabe gerade angeguckt, und wollte einen Rueckzieher machen, aber da Du mir zuvorgekommen bist, bitte schoen, erstmal die Beweisidee:
(Uebrigens, ich glaube, Microsoft unterstuetzt sowas prinzipiell nicht, fremde Dateien zu oeffnen, andersrum ginge es, aber in Word finde ich Formeln viel zu umstaendlich, mal schauen, was sich machen laesst.)
a)
Fuer n aus N, x aus ]0,2p gilt Sn k=1=sin((n+1/2)x)/2sin(x/2) - 1/2
(Hinweis: Betrachte erst Sn k=1e^(ikx) und dann die Darstellung cosx=Re(e^(ix))=(e^(ix)+e^(-ix))/2 )
b)
Fuer x aus ]0,2p[ gilt Sunendlich k=1sin(kx)/k = (p-x)/2
c)
Fuer alle x aus [0,2p] konvergiert die Reihe Sunendlich k=1 cos(kx)/k² gleichmaessig gegen ((x-p)/2)^2-p²/12
Daraus ergibt die Folgerung fuer x=0 Sunendlich k=11/K²=p²/6
Der komplette Beweis folgt (hoffentlich) bald, tritt mir vielleicht mal bei Gelegheit in den Hintern.
viele Gruesse
SpockGeiger |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 11. August, 2000 - 14:40: | 
|
Hallo Leute
Nachdem ich mir heute die Nacht um die Ohren gehauen habe, hier Beweis von a)
Der Rest folgt erst, wenn ich die Bugs entfernt habe (man, sind da viele Rechenfehler drin;)
Also, lest das, damit die Arbeit nicht umsonst war...
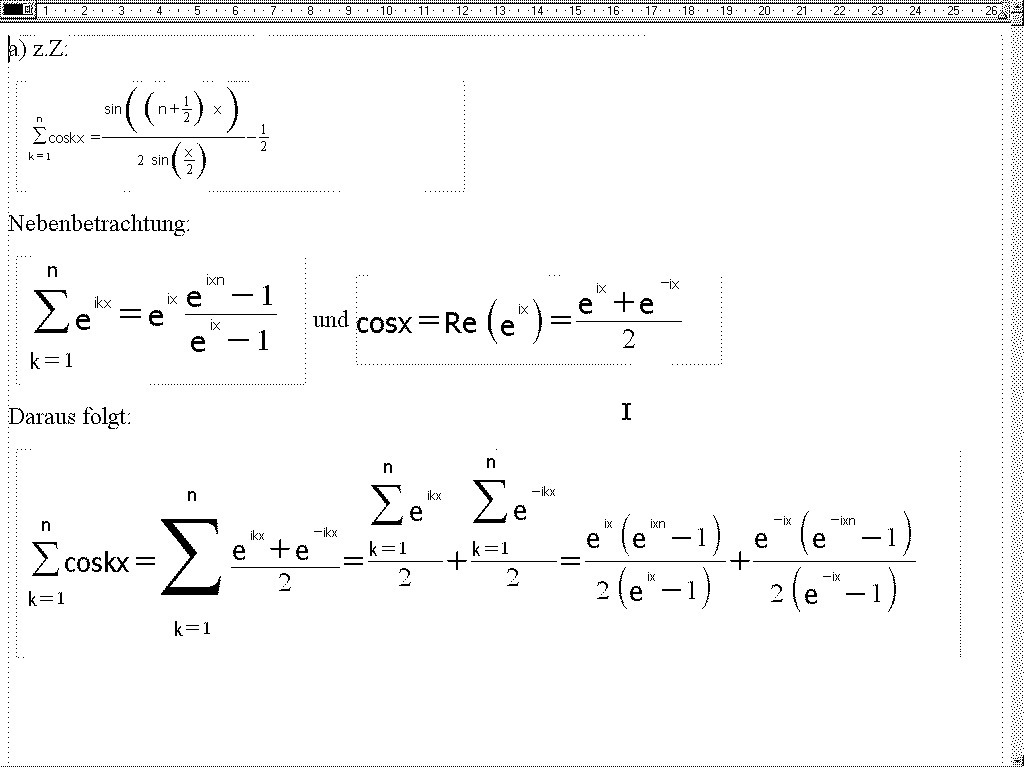
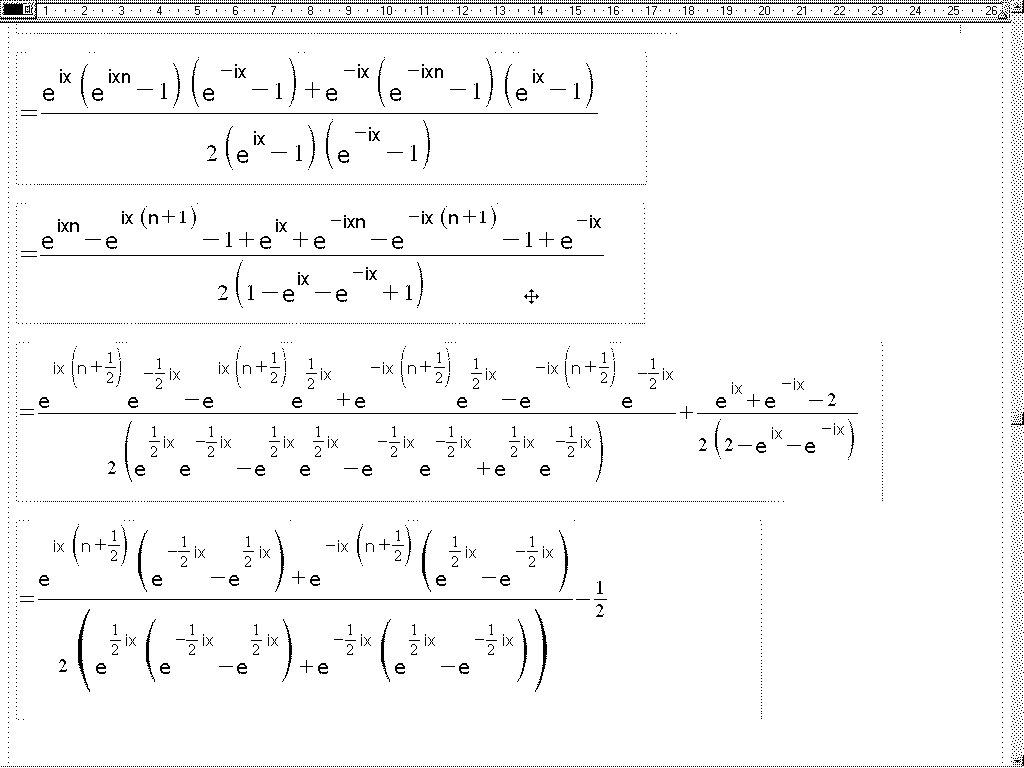
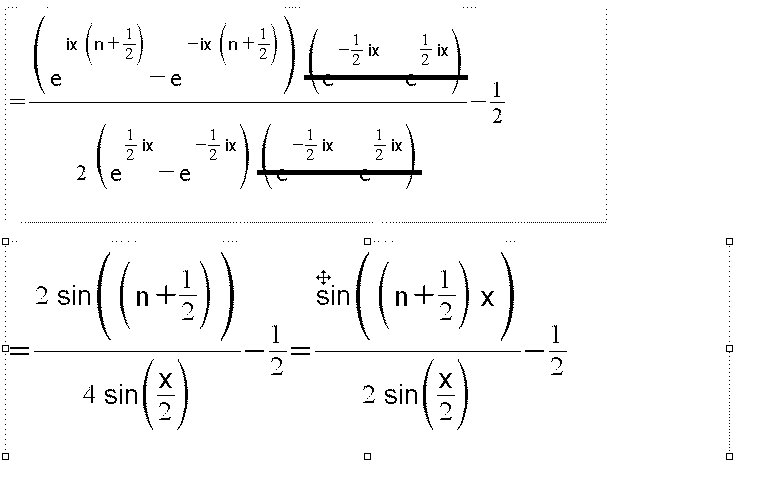
viele Gruesse
SpockGeiger |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 11. August, 2000 - 15:25: | 
|
Hi allerseits,
Die Summe S1 = Pi ^ 2 / 6 der unendlichen Reihe,
deren Glieder die reziproken Quadrate der natürlichen
Zahlen sind, kann auch elegant mittels Fourier-Reihen
ermittelt werden
Man erhält dabei noch mehr, als man wünscht,
nämlich auch die Summe S2 = Pi ^2 / 12 derjenigen
unendlichen Reihe, welche aus der vorigen durch Alternanz
der Vorzeichen entsteht.
Als Nebenprodukt ( nicht als Abfallprodukt ) erscheint noch die
Summe S3 = Pi ^ 2 / 90 der unendlichen Reihe mit den
Reziprokwerten der vierten Potenzen der natürlichen Zahlen
als Glieder.
Ausgangspunkt ist die periodische Funktion f(x) = x ^ 2
(Periode p = 2*Pi) ; abgeschlossenes Grundintervall
[ - Pi , Pi ], dann periodische Fortsetzung mit p.
Die Fourierkoeffizienten an und bn lassen sich leicht berechnen
Da die Funktion gerade ist { f(-x) = f(x) für alle x }.
sind alle bn null.
N.B. Alle folgenden Integrale sind bestimmte Integrale :
untere Grenze minus Pi, obere Grenze plus Pi
Für a0 und an , n = 1,2,3.....kommt:
a0 = 1 / Pi * int ( x ^ 2 * dx ) = 2 / 3 * ( Pi ) ^ 2
an = 1 / Pi * int ( x ^ 2 * cos (nx) * dx ) = (-1)^n * 4 / n ^2
Danach gilt nach Fourier:
f(x) = a0 / 2 + sum [an * cos(nx)] , der Summationsindex n
aller Summen läuft von 1 ad infinitum,
also:
x ^ 2 = (Pi) ^ 2 / 3 + 4 * sum [ (-1) ^ n * cos(n*x) / n ^ 2 ]
a) Setze x = 0 ; wir erhalten S2
b) Setze x = Pi , wir erhalten SA1
c) um S3 zu bekommen, verwenden wir die Besselsche Gleichung
(man kann in diesem Fall in der gleichnamigen Ungleichung das Gleichheitszeichen setzen !)
Die Gleichung lautet (Summe von 1 bis unendlich):
½ * ao^2 + sum [an ^ 2 + bn ^ 2] = 1 / Pi * int [f(x) ^ 2 * dx]
In unserem Fall:
2 / 9 * (Pi) ^ 4 + sum [16 / n ^ 4 ] = 2 / 5 * (Pi) ^ 4
Daraus berechnet man S3
Ueber die Konvergenz und die Uebereistimmung der Summe
mit f(x) brauchen wir uns keine Sorgen zu machen.
Der Theorie entnehmen wir:
Jede stückweise glatte Funktion mit der Periode 2*Pi lässt sich
in eine Fourier- Reihe entwickeln, die in jedem abgeschlossenen Stetigkeitsintervall absolut und gleichmässig konvergiert.
Dabei heisst eine Funktion f(x) in einem Intervall [a,b] der x-Achse
stückweise glatt, wenn f(x) und ihre Ableitung f '(x) bis auf
endlich viele Sprungstellen stetig sind.
Es gibt noch andere periodische Funktionen, mit deren Hilfe
durch die zugehörigen Fourier:Reihen S1 und andere Summen
berechnet werden können.
Die vorgeführte Berechnung sollte jedoch genügen
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 11. August, 2000 - 15:53: | 
|
Hallo
und weiter geht es , die elegante Methode lese ich mir gleich durch, erstmal Teil b:
Ach Moser, nebenbei, ab hier wird mein Bewei etwas brenslich, besonders am Ende, kannst Du Dir das mal anschauen, ob wirklich alles richtig ist?
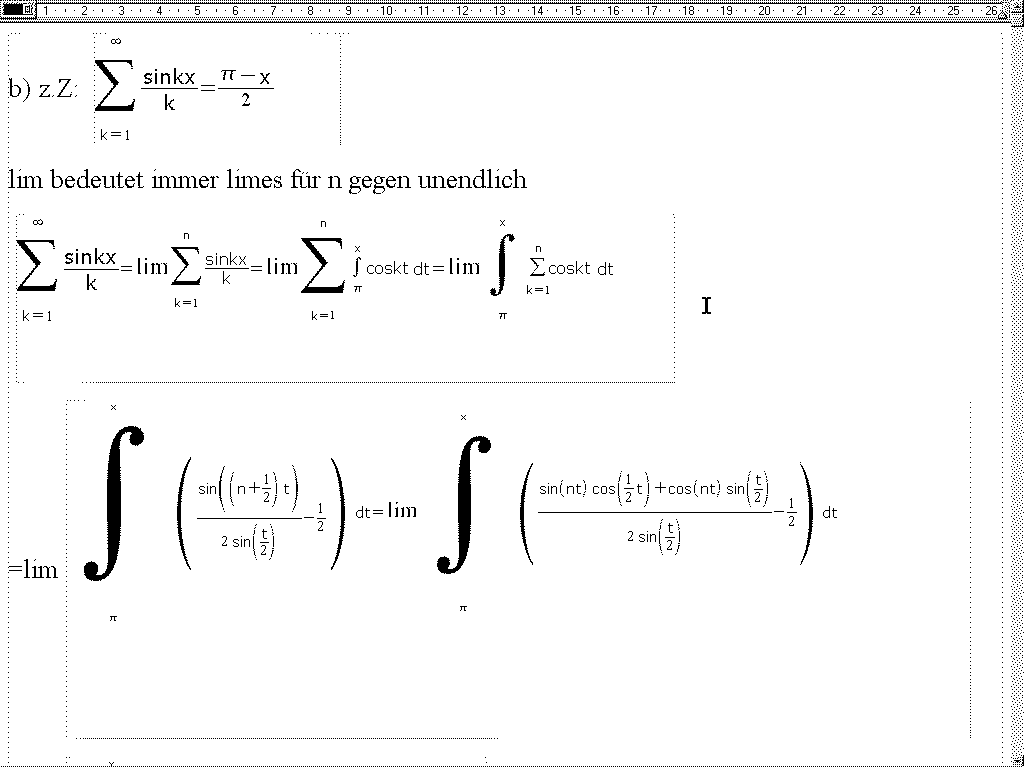
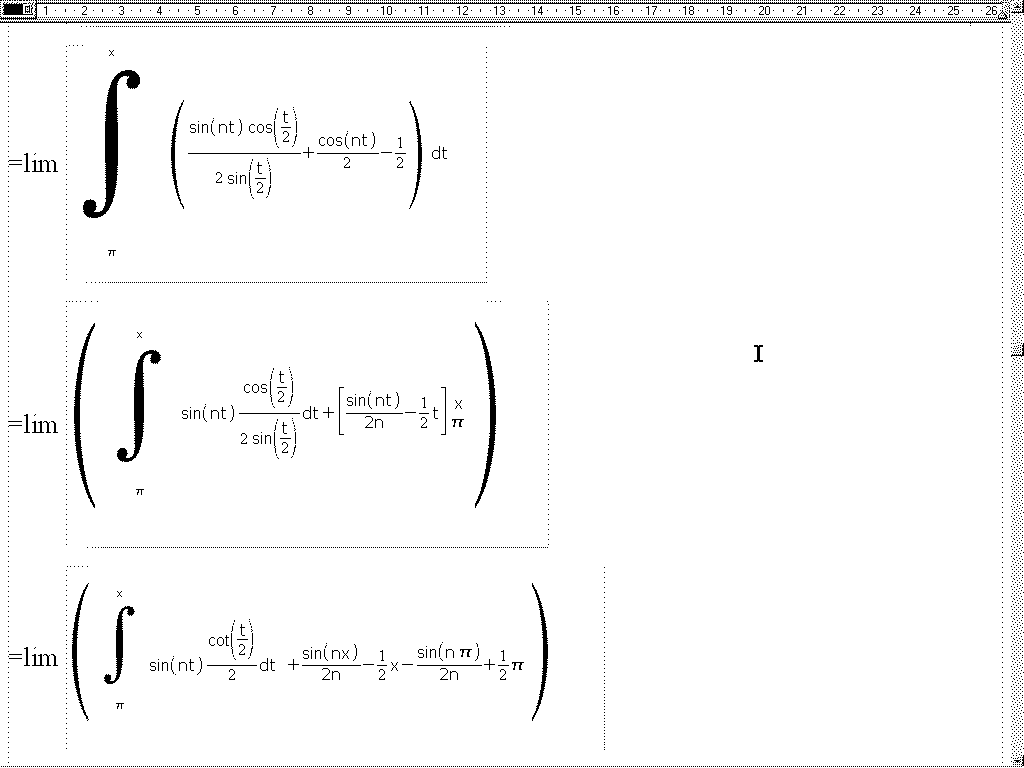
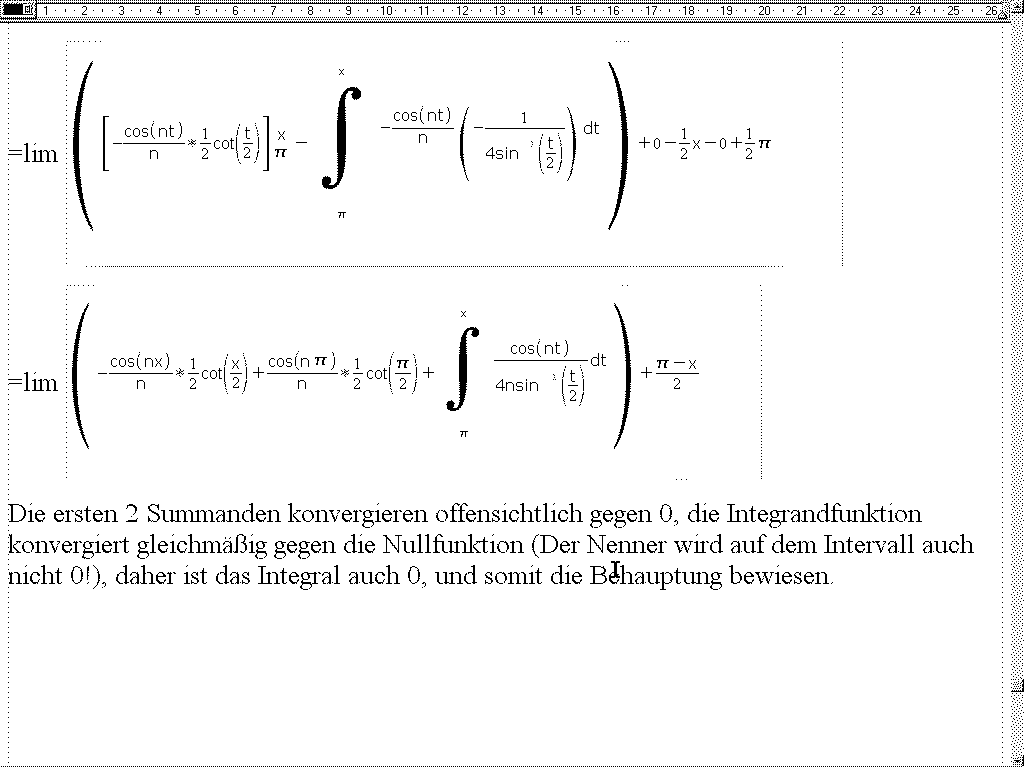
viele Gruesse
SpockGeiger |
    
Susi

| | Veröffentlicht am Freitag, den 11. August, 2000 - 17:21: | 
|
Na jetzt verstehe ich wenigsten warum im Buch steht: der Beweis ist schwierig! |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 11. August, 2000 - 17:35: | 
|
Hi
Den dritten Teil des Beweises bleibe ich Euch leider schuldig, da ich ihn falsch hatte. Vielleicht kann mir aber jemand von Euch helfen?
viele Gruesse
SpockGeiger |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 11. August, 2000 - 18:58: | 
|
Hi allerseits,
Cosine hat mit ihrer zweiten Frage eine kleine Lawine ausgelöst,
die an Volumen ständig zunimmt.
Es geschehen dabei neckische Dinge , wie man aus den beiden
Integralen ersehen kann ,die ich Euch präsentieren möchte.
Man ermittle durch Reihenentwicklung die bestimmten Integrale:
J1 = int [ 1 / x * ln ( 1 - x ) * dx ] untere Grenze 1 , obere Grenze 0,
J2 = int [ 1 / x * ln ( 1 + x ) * dx ] untere Grenze 0 , obere Grenze 1
Die Resultate lauten: J1 = (Pi) ^ 2 / 6 , J2 = (Pi) ^2 / 12.
Das Computerprogramm Maple V gibt diese Ergebnisse ebenfalss,
no problems !
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 11. August, 2000 - 22:07: | 
|
Hi allerseits,
Die Angelegenheit zieht immer grössere Kreise.
Es folgt nun ein kleiner Beitrag als Orientierung über die
Vielfalt der angezogenen Fragen
Mit s2, s3, s4,...sk,... seien die Summen der folgenden konvergenten unendlichen Reihen bezeichnet:
s2 = 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 +... ad infinitum
s3 = 1/1^3 + 1/2^3 + 1/3^3 + 1/4^3 + "
s4 = 1/1^4 + 1/2^4 + 1/3^4 +1/4^4 + "
...
sk = 1/1^k + 1/2^k + 1/3^k + 1/4^k + "
..............
Wir kennen bereits s2 = Pi ^ 2 / 6 und s4 = Pi ^ 4 / 90,
also noch recht wenig
Legendre hat die ersten 34 Summen s2 bis s35 auf je 16 Stellen
nach dem Komma berechnet , eine grossartige Leistung !
Die Folge der sk strebt übrigens mit wachsendem k fallend gegen 1.
Der Clou ist nun der ,dass die berühmte Eulerkonstante gamma
(num.Wert ~ 0.577215665) sich als unendliche Reihe mittels der
sk darstellen lässt:
gamma = 1 - 1 / 2 * s2 - 1 / 3 *s3 +1 / 4 * s4 - ..ad inf.
Diese Reihe ist sogar absolut konvergent
Von s1 war aus guten Gründen zunächst nicht die Rede
Die entsprechende Reihe divergiert ja ,wie wir alle wissen.
Es gibt jedoch eine tolle Darstellung in diesem Zusammenhang:
(der folgende Grenzwert bedeutet: n strebt gegen unendlich)
Lim [1 + 1 / 2 + 1 / 3 + 1 / 4 + 1 / 5 +.. + 1 / n - ln(n) ] =
= 1 / 2 * s2 -1 /3 * s3 + 1 / 4 * s4 - 1 / 5 * s 5 + ...
Die unendliche alternierende Reihe rechts vom Gleichheitszeichen
ist konvergent und stellt justement die Eulersche Konstante gamma dar
Das reicht für den Moment !
Mit freundlichen Grüßen
H.R.Moser,megamath.
... |
    
Cosine (Cosine)

| | Veröffentlicht am Freitag, den 11. August, 2000 - 22:56: | 
|
Boooaahhh...
Ich freue mich doch immer wieder, wenn meine kleinen Fragen Auslöser für lange Diskussionen bin. Danke an Spockgeier und Megamath, die so viel zu dem Thema geschrieben haben.
Ich werde mich bei Gelegenheit mal durch alles durcharbeiten, was hier so steht, aber nicht heute... Vielleicht morgen oder übermorgen...
Gute Nacht!
Euer (Ja, das ist kein Schreibfehler, da steht "Euer", nicht "Eure")
Cosine |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Freitag, den 11. August, 2000 - 23:35: | 
|
Hi
Ich wolte es ja auch schon fast sagen, dass Moser auch auf den Namen hereingefallen ist, und am Board nicht ganz auf dem laufenden ist ;)
viel Spaa beim Durcharbeiten...;)
viele Gruesse
SpockGeiger |
    
H.R.Moser,megamath.

| | Veröffentlicht am Samstag, den 12. August, 2000 - 21:48: | 
|
Hi allerseits,
Es folgt eine Ergänzung zu den in meiner vorhergehenden
Arbeit über die Summen s2, s3 , s4 ... der dort erwähnten
unendlichen Reihen.
Bemerkenswert:
Es besteht ein markanter Unterschied darin, ob die Indizes gerade
oder ungerade sind
Für gerade Indizes können die Summen ohne weiteres mittels
Fourier-Reihen ermittelt werden: als Ausgangsfunktion verwendet
man jeweils die Potenzfunktion f(x) = x ^ (2n) über dem
Grundintervall [ - Pi , Pi ] mit 2*Pi als Periode.
In der Reihendarstellung wird dann x durch Pi ersetzt
So erhält man für die ersten Summen mit geraden Indizes:
s2 = P i^ 2 / 6 ~ 1.644934
s4 = Pi ^ 4 / 90 ~ 1.082323
s6 = pi ^ 6 / 945 ~ 1.017343
s8 = Pi ^8 / 9450 ~ 1.004077
s10 =Pi ^10 / 93555 ~ 1.000995
u.s.w.
Für ungerade Indizes funktioniert dieses Verfahren nicht mehr.
Wir müssen direkt bei der Riemannschen Zetafunktion Zuflucht
nehmen und erhalten:
s3 = zeta(3) ~1.202057
s5 = zeta(5) ~1.036928
s7 = zeta(7) ~1.008349
s9 = zeta(9) ~1.002008
u.s.w.
Anhang
Es folgen weitere Beispiele, in welchen mit Fourier -Reihen
die Summen gewisser unendlicher Reihen bestimmt werden:
1. Ausgangsfunktion: f(x) = x ^ 3 , Grundintervall: [ - Pi , Pi ],
Periode 2 * Pi.
Die entsprechende Fourier - Reihe lautet:
f(x) = (Pi) ^ 2 / 3 + 4 * sum [(-1) ^ n * cos( n * x ) / ( n ^2 ) ]
n läuft von 1 bis unendlich..
Daraus folgt für x = 0: eine alternierende Reihe für ( Pi ) ^2 / 32
2. Ausgangsfunktion: f(x) = 4*a*x / T * (1 - x / T), Intervall [0 ,T],
Periode T = 2 * Pi / w.
Fourier-Entwicklung :
f(x) = 4 / (Pi) ^ 2 * a * { (Pi) ^ 2 / 6 - cos(w*x) - 1 / 4 * cos(2*w*x)
- 1 / 9 * cos (3 *w *x ) - .....ad inf.}
Setz man nun x = 0 , so erhält man wiederum unsere Reihe mit der
Summe (Pi ) ^ 2 / 6 ; bravo !
M.f.G.
H.R.Moser,megamath. |
    
Cosine (Cosine)

| | Veröffentlicht am Sonntag, den 13. August, 2000 - 20:52: | 
|
Nochmal Dankeschön!
Ich hatte jetzt endlich mal Zeit alle Lösungen durchzulesen.
Spockgeier: Ich habe jeden Schritt irgendwie nachvollziehen können, nur schade, dass der 3. Teil fehlt... Ich bezweifle allerdings, dass ich den 3.Teil beweisen und damit die Beweisführung vollenden kann...
megamath: Ich glaube einfach mal so, dass Deine Methode wesentlich eleganter ist, allerdings ist mein Wissen über Fourrier-Reihen noch sehr gering. Ich weiß eigentlich nur, dass es (manchmal?) möglich ist, periodische Funktionen als Summe von Sinussen und Cosinussen auszudrücken. Nun und da hört mein Wissen auch schon auf.
Allerdings fand ich die Geschichte mit s2, s3, s4 und der Eulerschen Konstante höchst interessant.
Vielen Dank nochmal, Ihr zwei!
Ciao
Cosine |
    
SpockGeiger (Spockgeiger)

| | Veröffentlicht am Sonntag, den 13. August, 2000 - 23:18: | 
|
Hallo
Vielen Dank an Cosine fuer den Feedback, ist immer wieder schoen...
an alle anderen: Koennte sich jemand den dritten Teil angucken???!!
Der Ansatz ist sicherlich, dass man den Ausdruck unter der Summe durch den aus Teil b ersetzt. Das geht, wenn man b integriert, aber mit den Grenzen komme ich ins schleudern, ich kriege es einfach nicht hin, eine Grenze fuer x so zu waehlen, das einer der Summanden 0 wird, das beste, was ich bisher hingekriegt habe, ist summe 1/k², aber da ich das noch nicht bewiesen habe, darf ich das ja auch nicht benutzen, also, bitte helft mir!
viele Gruesse
SpockGeiger |
    
H,R.Moser,megamath.

| | Veröffentlicht am Donnerstag, den 17. August, 2000 - 18:30: | 
|
Hi , Hi Cosine und Zaph,
Im Zusammenhang mit den von uns kürzlich betrachteten
unendlichen Reihen möchte ich Euch ein paar historische
Reminiszenzen nicht vorenthalten.
Die Aperçus entnehme ich dem ausgezeichneten 555 Seiten
starken Gedenkband zu Leonhard Euler, den der Schweizer
Halb-Kanton Baselstadt im Jahr1983 im Birkhäuser - Verlag ,
Basel, herausgegeben hat.
Eule und Bernoulli waren immerhin Basler !
Den hervorragend ausgestatteten Band sollte man unbedingt
anschaffen und allzeit griffbereit halten
Der betreffende Artikel stammt von Emil A. Fellmann
Er schreibt u.a.:
"Mit nicht geringem Stolz teilt Jakob Bernoulli in seinem Brief
vom 2.April 1737 Euler die Resultate
S4 = Pi ^ 4 / 90 und S6 = Pi ^ 6 / 945 mit, was Euler freundlich
mit der Korrektur eines Schreibfehlers
(Bernoulli schrieb bei S6 im Nenner 940)
und mit weiterführenden Resultaten quittierte:
S8 = Pi ^ 8 / 9450 , S10 = Pi ^ 10 , S12 = 691 * Pi ^12 / N ,
wobei er den Nenner der letzten Summe nicht mehr ausschreibt,
jedoch nachdrücklich darauf hinweist ,dass
< die Nenner zwar einem gewissen Gesetz zu folgen scheinen,
die Zähler jedoch bis anhin [gemeint ist bis S10] nur
zufällig = 1 gewesen > seien,
< denn die Summe S12 hat 691 im Zähler > ................
In diesem Zusammenhang sei vermerkt, dass sich Euler natürlich
auch an der Zetafunktion ungerader Argumente versucht hat, doch
gestand er Bernoulli im oben zitierten Brief schlicht :
<...Die ungeraden Potenzen kann ich nicht summieren, und ich
glaube nicht, dass ihre Summe von der Kreisquadratur abhängt >
(Uebersetzung : Emil A. Fellmann)
Erst in jüngster Zeit wurde der Irrationalitätsbeweis von Zeta(3)
geleistet
In seinem Brief vom 31. August 1740 an Euler gelangte Bernoulli
(mittels eines Theorems, über das er schon Jahrzehnte zuvor mit
Leibniz korrespondiert hatte)
zu den beachtlichen Teilresultaten:
sum (1 /x) ~ 14.392 726 722 865 723 ; Summation : x = 1 bis 10 ^ 6
sum (1/x) ~ 16 2/3 ; Summation: x = 1 bis 10 ^ 7
sum (1/x) ~ 19 , Summation x = 1 bis 10 ^ 8,
woraus das Wachstum bereits ersichtlich ist:
Wächst die Gliederzahl um das Zehnfache, so nimmt die Summe
um den natürlichen Logarithmus von 10 zu.
Ende Zitat und satis !
Mit freundlichen Grüßen
Hans Rudolf Moser |
    
Niti

| | Veröffentlicht am Dienstag, den 28. November, 2000 - 20:16: | 
|
Ich hätte da mal ein Problem:
Aufgabe:
Eine Tiefbohrung iwrd niedergebracht.Am ersten tag schafft das Bohrteam 180m, an jedem weiten tag sind es aufgrund schwieriger verhältnisse 5m weniger als am voorherigen Tag.
Nach wieviel tagen wird eine Tiefe von 2475m erreicht?? |
    
mori

| | Veröffentlicht am Mittwoch, den 29. November, 2000 - 08:42: | 
|
Bitte neue Fragen nicht an alte anhängen sondern einen neuen Beitrag öffnen! |
|