| Autor |
Beitrag |
    
SpockGeiger

| | Veröffentlicht am Freitag, den 21. April, 2000 - 20:09: | 
|
Hi Jungs
Ich hab mal wieder ne ganz harte Nuss fuer Euch:
ich habe gerade folgendes erfolgreich bewiesen:
Summe(k=1..n, cos(kx)) = sin((n+1/2)x)/2sin(x/2) - 1/2
Das war nur eine Teilaufgabe und sollte mich, so denke ich, auf den Beweis folgender Gleichung fuehren:
Summe(k=1..unendlich, sin(kx)/k ) = (pi - x)/2
Ich moechte eigentlich gar keine vollstaendige Loesung, deswegen koennt Ihr Euch unnoetige Tipparbeit sparen, ich braeuchte nur einen brauchbaren Ansatz.
Da ich schon dabei bin: Gibt es eine Formel fuer summe(k=1..n,1/k)???
Ich danke Euch schon vielmals im voraus
MfG
SpockGeiger |
    
Ingo

| | Veröffentlicht am Freitag, den 21. April, 2000 - 20:49: | 
|
Der Tip lautet
òpx cos(kt) dt = sin(kx)/k |
    
SpockGeiger

| | Veröffentlicht am Samstag, den 22. April, 2000 - 16:45: | 
|
Hi
Danke schoen erstmal, hat mich erstmal etwas weitergebracht. Dabei komme zur folgenden Umformung:
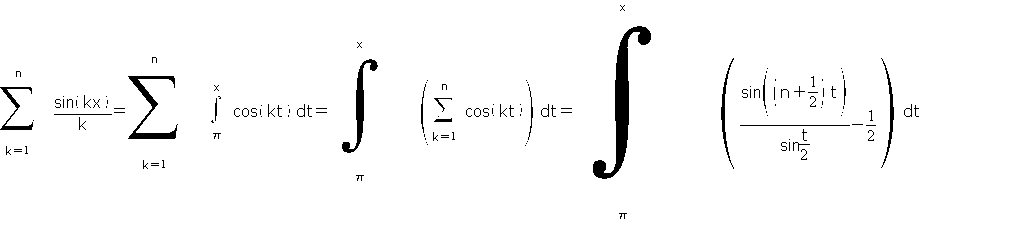
Bei der Berechnung des linken Summanden komme ich aber nur soweit:
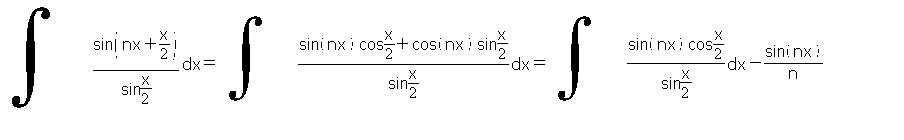
Wer kann mir weiterhelfen?
Danke schoen im voraus
SpockGeiger |
    
Ingo

| | Veröffentlicht am Samstag, den 22. April, 2000 - 22:25: | 
|
2.Tip : Zeige durch partielle Integration,daß
lim òab f(x)sin(kx) dx =0
k->¥
Stammt übrigens alles aus Analysis I. von Otto Forster(§19) |
    
H.R.Moser,megamath.

| | Veröffentlicht am Sonntag, den 23. April, 2000 - 19:48: | 
|
Hi SpokeGeiger,
Die harte Nuss, die Du neulich ins Board gestellt hast, ist noch keineswegs geknackt. Um die harte Schale zu brechen, solltest Du ganz andere Mittel einsetzen !
Die Aufgabe gehört zum Themenbereich "Fourierreihen".
Wir wollen sie neu formulieren, und es schadet sicher nichts ,wenn wir sie noch geringfügig erweitern und den Lösungsweg zu Instruktionszwecken etwas genauer unter die Lupe nehmen. Also:
a) Entwickle die Funktion f(x) = (Pi - x ) / 2 , Intervall [0, 2*Pi] ,
Periode 2* Pi , in eine Fourierreihe , und kontolliere, ob die Dirichletsche
Bedingung erfüllt ist.
b) Wende die Formel von Parseval auf die Fourierentwicklung von f(x) an
(betreffend Parseval: siehe im Archiv unter Nr 2633 nach)
c) Stelle mit Hilfe der Fourierschen Reihe für f(x) die Zahl Pi / 4 als Summe
einer unendlichen Sinus-Reihe dar.
Skizze einer Lösung.
Zu a) Berechnung der Fourier- Koeffzienten ao, an , bn :
ao = 1/(2*Pi) * int (f(x) * dx) = 1 / (2* Pi) * int ((Pi-x) / 2 * dx) = 0
Untere Grenzen je null, obere Grenzen je 2*Pi ; dasselbe gilt auch für alle
folgenden bestimmten Integrale !
an = 1/Pi * int( f(x) * cos(n x)*dx) = 1/ Pi * int( (Pi - x) / 2 * cos(nx)*dx)
= 0; das war zu erwarten ,da f(x) nach erfolgter periodischer
Erweiterung (Periode 2*Pi ) bezüglich des Nullpunktes symmetrisch ist
bn = 1/Pi * int (f(x) * sin(n x )*dx) = 1/Pi*int( (Pi - x) / 2*sin(nx)*dx)
= 1 / n
Bei der Berechnung der Integrale für an und bn verwendet man am
besten die Methode der partiellen Integration Ausführliche Berechnungen
werden auf Wunsch nachgeliefert.
Mit diesen Koeffizienten kann die Fourierreihe sofort angeschrieben werden.
f(x = ao + sum ( an * cos (nx) + bn * sin (nx) ), n = 1 bis .unendlich ).
Es kommt ,wie von Geisterhand:
sum ( sin ( n * x ) / n , n = 1.. infinity) = (Pi - x) / 2 ; bravo !
f(x) ist im abgeschlossenen Intervall [0, 2*Pi] als lineare Funktion stetig differenzierbar und sie ist periodisch mit der Periode 2* Pi. fortsetzbar. Die Funktionswerte an den Sprungstellen werden so.definiert :.f (k*2Pi ) = 0.
Da die Bedingung von Dirichlet erfüllt ist , stellt die Reihe für alle x-Werte
wirklich die gegebene Funktion f(x) dar, wzbw.
b) Wir berechnen einerseits S = ao + sum (an ^2 ° + bn^2 ) / 2 , n = 1 bis unendlich. Es ergibt sich mit der bekannten Reihe der reziproken Quadratzahlen, deren Summe bekanntlich Pi ^2 / 6 ist: S = Pi ^2/12
(S = sum 1 / n^2 , n = 1 bis unendlich = Pi ^2 / 6)
Andrerseits berechnen wir :
T = 1 / (2*Pi) * int ((f(x)^2)*dx) , Grenzen : 0 bis 2Pi.:Man findet leicht:
T = Pi ^2 / 12 , somit gilt S = T , und die Gleichung von Parseval ist erfüllt ,
wie nicht anders zu erwarten war !
c) Setze in der unendlichen Reihe x =Pi / 2 ein, und Du gewinnst die Beziehung:
sum ( sin ( n* Pi / 2 ) / n , n = 1 bis.unendlich ) = Pi / 4 .
------------------------------------------------------------------------------------------------
Auf Deine Frage bezüglich der Summe der Reziproken 1 + ½ + 1/3 + .. + 1 / n
soll später eingegangen werden !
-------------------------------------------------------------------------------------------------
Bis dahin
Ostergrüsse von H.R.
------------------------------------------------------------------------------------------------- |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 24. April, 2000 - 16:50: | 
|
Hi SpockGeiger,
Es folgt nun eine Antwort auf Deine Schlussfrage vom 21.4. a.c.
Für die Summe S1(n) der sukzessiven Reziprokwerte der
natürlichen Zahlen von 1 bis und mit n gibt es keine geschlossene
Formel, welche mit den gängigen Funktionen auskäme.
Jedoch wird in diesem Zusammenhang oft von dem in der folgenden
Formel verpackten Grenzwert Gebrauch gemacht:
C = l i m ( sum(1 / k , k = 1 bis n ) - ln n ) , für n strebt gegen unendlich (EU)
C ist die Eulersche Konstante mit dem Näherungswert 0.5772156649.
An einem Beispiel wollen wir die Wirksamkeit dieser Formel uns zu Gemüte führen:
Sei n = 10^6, wir berechnen S+(10^6) mit dem CAS Maple V und danach
mit der Formel (EU)
Maple V gibt den Näherungswert 14.39272672, die Formel (EU) den Wert
14.39272622 (!)
Grundsätzlich sollte man nur solche Formeln und Sätze gebrauchen,
deren Herleitung man kennt.
Daher sollen im Anschluss ein möglicher Beweis der Formel (EU) skizziert werden
------------------------------------------------------------------------------------------
Vorbemerkung. Es sollen die folgenden Bezeichnungen benützt werden:
S1(n) = 1 + 1 / 2 + 1 / 3 + 1 / 4 + ... + 1 / n
S2(n) = 1 + 1 / 2 ^ 2 + 1 / 3 ^2 + 1 / 4 ^ 2 + .. .+ 1 / n ^ 2
S3(n) = 1 + 1 / 2 ^ 3 + 1 / 3 ^ 3 + 1 / 4 ^ 3 + +. 1 / n ^3
........................ u . s w . .............................................................................
Für n gegen unendlich konvergieren die entsprechenden unendlichen Reihen
alle, ausser der ersten; die harmonische Reihe ist bekanntlich divergent.
Im folgenden wird nun aber nachgewiesen, dass d(n) = S1(n) - ln n für n
gegen unendlich ebenfalls konvergiert. Das Beweis geht so :
Wir benützen eine bekannte unendliche Reihe für die Darstellung des
Terms ln(u+1) -lnu , gültig für 0 < u < = 1
ln (u+1) - ln u = ln (1 + 1/u) = 1/u - 1/(2 u^2) + 1/ ( 3 u^3) - 1( 4 u ^4) + ..
In diese Entwicklung setzen wir der Reihe nach für u die Werte
u = 1,2,3,4.... (n-1 ) ein und erhalten:
ln 2 = 1 -1 / 2 + 1 / 3 - 1 / 4 + ..
ln3 - ln2 = 1 / 2 - 1 / ( 2*2^2) + 1 / ( 3 * 2^3 ) - 1 / ( 4 * 2^4) +..
ln 4 - ln 3 = 1 / 3 - 1 / (2*3^2) + 1 / ( 3 * 3 ^3) - 1 / ( 4 * 3^4) +..
............u s w ..........................
ln n-ln (n-1)=1/(n-1) -1 / (2*(n-1)^2) + 1 / ( 3*(n-1)^3 - 1 / (4*(n-1)^4)+..
ln (n+1) - ln n =1/n - 1 / (2*n^2) + 1 / ( 3*n^3) - 1 / (4*n^4) +..
Durch Addition dieser Gleichungen kommt:
ln (n + 1 ) = S1(n) - 1 / 2 * S2(n) + 1 / 3 * S3(n) - 1 / 4 * S4(n) + ..
Auflösung nach S1(n) ergibt:
S1(n) = ln (n+1) + 1 / 2 * S2 (n) - 1/3 * S3 (n) + 1 / 4 * S 4 ( n ) - .. oder:
Links und rechts subtrahieren wir ln n und schreiben ln((n+1) / n)
für ln (n +1) - ln n . So erhalten wir schliesslich:
S1(n) - ln n = ln ((n+1) / n) + 1 / 2 * S2(n) - 1/3*S3(n) + 1 / 4 * S4 (n)- .
Jetzt soll n gegen unendlich streben. Was passiert ?
Der Logarithmus im ersten Summand rechts strebt gegen null , der Rest der rechten Seite, eine alternierende Reihe aus einzelnen konvergenten Reihen konvergiert. Die Summe der rechten Seite hat einen bestimmten endlichen Grenzwert: es ist dies die mit C bezeichnete Eulersche Konstante :
C = l i m ( S1(n) - ln n ) = 1 / 2 * S2(n) - 1 / 3 *S3(n) +-- , n gegen unendlich.
---------------------------------------------------------------------------------------------
Anmerkung: Die Summen der Reihen SJ(n) ,n gegen unendlich, bilden mit wachsenden Werten von J eine streng monoton fallende Folge
mit der Zahl 1 als unterer Grenze. Die ersten 35 Zahlen dieser Folge hat bereits Adrien Marie Legendre je auf 16 Stellen nach dem Komma berechnet,
eine tolle Leistung mit den damals (1806) zur Verfügung stehenden Mitteln !
Das erste Glied dieser Folge kennen wir wohl alle: es ist die Summe der unendlichen Reihe der reziproken Quadratzahlen , also Pi ^2 / 6 = 1.644934.
Diese Summe spielte bereits weiter oben, bei der Behandlung der Gleichung
von Parseval, eine Rolle, und damit hat sich der Kreis geschlossen
-------------------------------------------------------------------------------------------------
Mit den besten Wünschen für jegliches Studium
H.R.Moser,megamath.
------------------------------------------------------------------------------------------------- |
    
SpockGeiger

| | Veröffentlicht am Montag, den 24. April, 2000 - 19:37: | 
|
Hi
vielen Dank fuer Deine ausfuehrlichen Antworten, wobei mir das erstere etwas zu hoch war, den Stoff haben wir noch nicht durchgemacht. Das zweite habe ich auf dem gleichen Uebungszettel schon bewiesen, allerdings mit Integralvergleichskriterium.
Nochmals danke und nachtraeglich Frohe Ostern!
MfG
SpockGeiger |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 24. April, 2000 - 21:36: | 
|
Hi SpockGeiger,
Besten Dank für das Echo !
Eleganz ist ansonsten eine exklusive Angelegenheit von Modehäusern (z.B. in Paris oder Rom). Gleichwohl ging ich auf die Suche nach einem
etwas ansprechenderen Beweis der letzten Formel, in der die
Eulersche Konstante auftritt.
Hier das Resultat meiner Recherche:
Man beweist zuerst die Relation :
ln (1 + 1 / k ) = 1 / k + Theta ( k) / k ^ 2 , k = 1, 2, 3 ,.. mit der Klausel:
Absolutbetrag von Theta (k) < = 1
Man setzt in dieser Beziehung der Reihe nach k = 1 , 2 , 3.., n-1 ein und addiert die n - 1 Gleichungen. Aus dem Ergebnis findet man die Beziehung
Lim (( sum 1 / k , k = 1 bis n) - ln n) = c für n gegen unendlich.
Dabei ist c ein noch zu bestimmender endlicher Wert.
Mit freundlichen Grüßen.
HR.
------------------------------------------------------------------------------------------------- |
    
H.R.Moser,megamath.

| | Veröffentlicht am Dienstag, den 25. April, 2000 - 19:16: | 
|
Hi SpockGeiger,
Vielleicht interessieren sich einige Teilnehmer am Forum, seien es nun Fachleute oder Hobbymathematiker, für weitere Events bezüglich der Eulerschen Konstanten C.
Zu Vergleichszwecken sei daher auch noch die von Dir letzthin erwähnte Methode des Integralkriteriums zur Herleitung des Grenzwertes, mit welcher
die Eulerschen Konstante definiert wird, vorgeführt.
Dieses Integralkriterium stammt von Maclaurin und Cauchy und dient zur Feststellung der Konvergenz oder auch der Divergenz von
unendlichen Reihen mit nicht negativen Gliedern.
f(x) sei eine positive, monoton fallende Funktion in dem benützten Bereich. Dann gilt für die natürlichen Zahlen n und N, mit n 1 , dasselbe gilt somit für die unendliche Reihe.
Letztere stellt übrigens im Falle der Konvergenz die aus der Zahlentheorie und aus der Funktionentheorie bekannte Zetafunktion Zeta(s) (s>1) dar
Es gelten die bemerkenswerten Relationen: Zeta ( 2 ) = Pi ^2 / 6 ,
Zeta ( 4 ) = Pi ^ 4 / 90 , Zeta ( 6 ) = P i ^ 6 / 945 ... u.s.w.
Ueber die Zeta -Werte ungerader Argumente ist nichts derartiges bekannt.
Nun setzen wir s = 1 ein. Die (Ugl I) liefert:
Int (1 / x *dx) (untere Grenze 1,obere Grenze N) < = sum (1 / k , k=1 bis N) < =
1 + int ( 1 / x * dx) (untere Grenze 1 , obere Grenze N) ,oder
ln N < = sum (1 / k , k = 1 bis N) < = 1 + ln N. Es gilt somit:
0 < = sum ( 1 / k , k = 1 bis N ) - ln N < = 1.
Da die Folge, gebildet mit dem Term zwischen den Ungleichheitszeichen, mit wachsenden Werten von N monoton fällt und ja nach unten beschränkt ist,
ist sie nach einem bekannten Satz konvergent; der Grenzwert sei C.
Diese Konstante C ist der gesuchte Ansprechpartner, nämlich die Eulersche Konstante.
--------------------------------------------------------------------------------------------
Damit ist auch diese Methode erfolgreich zu Ende geführt.
M.f.G
H.R.
________________________________________________________________
. |
|