| Autor |
Beitrag |
    
Willi

| | Veröffentlicht am Sonntag, den 09. April, 2000 - 14:59: | 
|
Hi!
Unser Lehrer (Realgymnasium) hat uns bis Do, 13.04., eine Knacknuss aufgegeben, an der wir in unserer Matherunde verzweifeln.
Zwei Leitungsmasten von je 27 m Höhe stehen auf gleichmäßig ansteigendem Gelände. Ihre waagrechte Entfernung beträgt 200 m, ihr Höhenunterschied 15 m. Visiert man von der Spitze A des ersten Mastes der Leitung entlang, so trifft die Visierlinie den zweiten Mast in einem Punkt C, der 9 m tiefer liegt als A.
In welchem Punkt kommt die Leitung dem Erdboden am nächsten, wenn man sie näherungsweise als Parabel mit lotrechter Achse auffasst? Wie groß ist der minimale Abstand?
Ganz ehrlich, wir verstehen nicht einmal die Angabe.
Ist da jemand, der uns helfen kann.
Willi für die ganze 8b
Danke! |
    
franz

| | Veröffentlicht am Sonntag, den 09. April, 2000 - 15:21: | 
|
Kennst Du Differentialrechnung? |
    
Anonym

| | Veröffentlicht am Sonntag, den 09. April, 2000 - 16:53: | 
|
woher denn, er ist doch erst in der 8. |
    
Willi

| | Veröffentlicht am Sonntag, den 09. April, 2000 - 18:11: | 
|
Hi!
Hier ist Willi.
Ja, Franz, wir kennen die Differantialrechnung, die 8. ist in Österreich die Abiturklasse.
Ciao |
    
franz

| | Veröffentlicht am Sonntag, den 09. April, 2000 - 23:15: | 
|
Den Ursprung würde ich in den Fußpunkt von A legen. Masthöhe H, waagerechter Entfernung zum nächsten e, Höhenunterschied h, "Peildifferenz" d. Stromleitung y(x)=!ax²+bx+c. Drei Unbekannte, drei Bedingungen: y(0)=H; y(e)=h+H; y'(0)=d/e. Daraus die Parabel y(x).
Abstand Hang g(x)=(h/e)*x zur Parabel? Ansatz: Die Normale auf der Geraden g im Punkt, der zu xo gehört - N(x)=-(e/h)*(x-x0)+(h/e)*x0 - zum Schnitt bringen mit der Parabel, Abstand bestimmen, Minimum suchen. Vielleicht gibt's eine einfachere Lösung? |
    
Fern

| | Veröffentlicht am Montag, den 10. April, 2000 - 08:40: | 
|
Hallo Willi,
Wir legen ein Koordinatensystem mit Ursprung im Fußpunkt des ersten Mastes, x-Achse horizontal, y-Achse vertikal.
Mastspitzen seien die Punkte A und B.
Dann sind die Koordinaten dieser Punkte:
A=(0, 27)
B=(200, 42)
Eine Parabel mit vertikaler Achse hat die Gleichung:
y=ax²+bx+c
Ableitung: y'=2ax+b
Bedingungen:
durch A: 27=c
durch B: 42=200²a+200b+c
Tangente in A hat die Neigung: -9/200 dies ist y'
-9/200=b
===================
Also a=3/5000
b=-9/200
c=27
Gleichung der Parabel: y=3/5000x²-(9/200)x+27
=============================================
Nun ist es einfach den Bodennächsten Punkt B zu finden:
er liegt genau zwischen den Masten, also bei x=100
Für x=100 in die Parabelgleichung eingesetzt:
y-Höhe des Punktes B = 28,5 m
Bodenhöhe für x=100 ist 7,5 m
B liegt also genau 21 m vertikal über dem Boden.
Um den Bodennächsten Abstand zu erhalten, multiplizieren wir wir nochmit dem cos(alpha), wobei alpha der Anstiegswinkel des Bodens ist.
tan(alpha)=15/200
21*cos(alpha)=20,941 m
========================
Dies ist der minimale Abstand des Kabels vom Boden. |
    
franz

| | Veröffentlicht am Montag, den 10. April, 2000 - 09:51: | 
|
Bemerkenswert an dieser eleganten Lösung ist, daß die Leitung ihren bodennächsten Punkt in der Mitte, bei e/2, erreicht. Dort hat die Tangente dieselbe Steigung wie der Boden. F. |
    
Zaph

| | Veröffentlicht am Montag, den 10. April, 2000 - 10:20: | 
|
Haargenau, man muss die Bodenlinie parallel verschieben, bis sie die Leitung trifft. Also ist die Gleichung
y' = 15/200
zu lösen. Und dann erhält man in der Tat x=100 für den bodennächsten Punkt. Wieso das ausgerechnet die Mitte zwischen den beiden Masten ist, ist mir anschaulich erstmal nicht klar. |
    
franz

| | Veröffentlicht am Montag, den 10. April, 2000 - 11:13: | 
|
Gesucht x: y'(x)=(y(e)-y(0))/e -> x=e/2 |
    
Zaph

| | Veröffentlicht am Montag, den 10. April, 2000 - 13:13: | 
|
Ja klar, ausrechnen kann ich das auch. Aber folgt das auch, ohne rechnen zu müssen?? |
    
Willi

| | Veröffentlicht am Montag, den 10. April, 2000 - 13:43: | 
|
Hallo Fern & Co!
Ihr seid super und wir freuen uns schon auf das Gesicht unseres Lehrers!!!!
Danke |
    
Fern

| | Veröffentlicht am Montag, den 10. April, 2000 - 18:20: | 
|
Hallo,
Ich war den ganzen Tag nicht zu Hause, deshalb erst jetzt eine Bemerkung zu den Kommentaren:
Eine Gerade, die parallel zur Parabelachse liegt, wird Parabeldurchmesser genannt.
Ein Parabeldurchmesser halbiert sie Sehnen, die zur Tangente im Endpunkt des Durchmessers parallel liegen.
In unserem Beispiel liegen die beiden Mastspitzen A und B auf einer Parabelsehne, die parallel zum Boden ist und damit auch parallel zur Tangente im bodennächsten Punkt. Der Mittelpunkt dieser Sehne liegt also genau senkrecht über dem Tangentenpunkt.
Siehe meine etwas schematische Skizze.
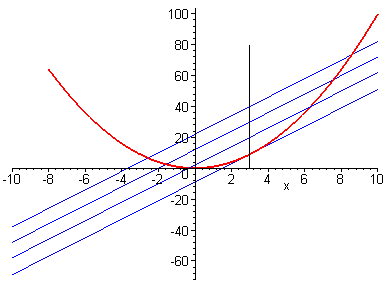 |
    
franz

| | Veröffentlicht am Montag, den 10. April, 2000 - 18:23: | 
|
Hallo Zaph, genügen Dir Mittelwertsatz und lineares Verhalten der Ableitung? F. |
    
Zaph

| | Veröffentlicht am Montag, den 10. April, 2000 - 22:10: | 
|
Fern, ok, das muss man natürlich erst einmal wissen. Habe ich aber wahrscheinlich nach einer Woche wieder vergessen.
Franz, der Mittelwertsatz sagt nur etwas über die Existenz, d.h. dass es einen Punkt der Leitung gibt, wo die Steigung exakt mit der Steigung der Bodenlinie übereinstimmt. Der Mittelwertsatz sagt nichts darüber, wo dieser Punkt zu finden ist.
Wenn man von der Vereinfachung abgeht, dass die Leitung eine Parabel bildet, und nicht eine "Kettenlinie" (Cosinus-Hyperbolicus-Funktion) habe ich so meine Zweifel, ob der Punkt immer noch in der Mitte liegt. |
    
franz

| | Veröffentlicht am Dienstag, den 11. April, 2000 - 08:16: | 
|
Zaph, die Ableitung der quadratischen Funktion ist linear und erreicht deshalb in der Mitte ihren mittleren Wert, jenen Mittelwert. F. |
    
Fern

| | Veröffentlicht am Dienstag, den 11. April, 2000 - 09:11: | 
|
Hi Zaph,
franz hat Recht mit der Begründung durch die Linearität der ersten Ableitung.
Bei einer Kettenlinie ist die Ableitung (=sinh(x)) nicht mehr linear und der bodennächste Punkt daher mit Sicherheit nicht in der Mitte. |
    
Zaph

| | Veröffentlicht am Mittwoch, den 12. April, 2000 - 18:02: | 
|
Hi Franz und Fern, auch auf die Gefahr, dass ich euch nerve oder langweile: aber ich muss noch einmal Einspruch erheben.
Aus der Linearität der ersten Ableitung folgt
(y'(0) + y'(e))/2 = y'(e/2).
Wir wollen aber
y'(e/2) = (y(e) - y(0))/e.
Es bleibt also immer noch nachzurechnen, dass
(y'(0) + y'(e))/2 = (y(e) - y(0))/e.
Da kann man dann aber auch gleich die Gleichung
y'(x) = (y(e) - y(0))/e
nach x auflösen, was x = e/2 liefert. (Diese Methode hat den Vorteil, dass sie universell ist und nicht auf quadratische Funktionen y beschränkt ist.)
Gruß Z. |
    
Fern

| | Veröffentlicht am Mittwoch, den 12. April, 2000 - 20:27: | 
|
Hi Zaph,
Ich versuch's mal bildlich:
Wir betrachten die rote Parabel: die Ordinaten der blauen Geraden sind die Steigung der Parabel an der jeweiligen Stelle, also für den Punkt P1 ist die Steigung negativ und entspricht dem linken, dicken, blauen Strich. Gleiches gilt für P2.
Die mittlere Steigung der Parabel zwischen P1 und P2 ist die Steigung der schwarzen Verbindungslinie. Wegen der Linearität der Ableitung ist diese mittlere Steigung aber auch der Mittelwert der beiden dicken blauen Striche. Es ist die Ordinate der blauen Linie, die genau in der Mitte der x-Werte von P1, P2 liegt. (Grüne Linie entspricht der mittleren Steigung zwischen P1 und P2).
Das heißt: die Parabel hat für xM die gleiche Steigung wie die Steigung der schwarzen Geraden von P1 bis P2.
 |
    
Fern

| | Veröffentlicht am Mittwoch, den 12. April, 2000 - 20:30: | 
|
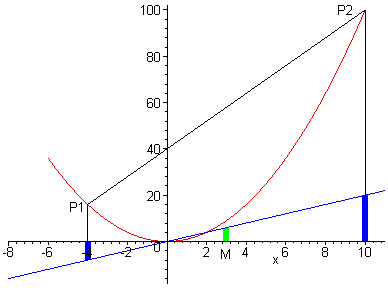 |
    
franz

| | Veröffentlicht am Donnerstag, den 13. April, 2000 - 09:49: | 
|
Hallo allerseits, das gleiche ohne Bild: Es geht um eine anschauliche Erklärung dafür, daß bei einer Parabel die Tangente an einen Punkt des Graphen P(x) parallel zu der Geraden durch zwei Punkte P1(x-a) und P2(x+a) ist, für alle x und a. Richtig?
Die Änderungen des Anstiegs bei x-a beziehungsweise x+a gegenüber x sind wegen der Linearität der Ableitungsfunktion gleich und entgegengesetzt. Also 1/2*(y'(x-a)+y'(x+a))=y'(x). Geometrisch gesprochen sind die Sekanten durch die gleichentfernten Punkte P1P2 parallel der Tangente durch P, also (y(x+a)-y(x-a)/(2a)=y'(x). qed.
Gruß F. |
    
Zaph

| | Veröffentlicht am Freitag, den 14. April, 2000 - 17:49: | 
|
Hi noch mal, vielen Dank für eure Mühe!
Franz' Argument kann ich nachvollziehen, obwohl hier wohl etwas mehr als die Linearität der Ableitung eine Rolle spielt.
Bei Fern habe ich Schwierigkeiten. Z.B. "die mittlere Steigung der Parabel zwischen P1 und P2 ist die Steigung der schwarzen Verbindungslinie". Auch ich bin ein Fan von Bildchen, sagen sie doch oft mehr als 100 Worte. Und von deinen Graphiken, Fern, bin ich immer begeistert. Aber wenn es drum geht, heißt es dann "Butter bei die Fische", d.h. ein formaler Beweis ist gesucht. Kannst du allein aus der Voraussetzung, dass die Ableitung linear ist (ohne Verwendung der Tatsache, dass y(x) eine quadratische Parabel ist) beweisen, dass y'(e/2) = (y(e) - y(0))/e gilt? |
    
Fern

| | Veröffentlicht am Freitag, den 14. April, 2000 - 19:55: | 
|
Hi Zaph,
Noch ein Bildchen:

Betrachten wir die Fläche unter der blauen Geraden von x=4 bis zu einem variablen Wert x, so stellt diese Fläche eine Funktion dar, die den Ordinaten der roten Parabel entspricht. Der Flächeninhalt nimmt quadratisch mit x zu.
Nun ersetzen wir diese Fläche durch die Fläche unter der grünen (horizontalen) Geraden: sie entspricht den Ordinaten der schwarzen Geraden von P1 nach P2.
Da "grüne Fläche" und "blaue Fläche" flächengleich sind, entspricht auch die Steigung P1-P2 der mittleren Steigung der Kurve.
Die grüne Ordinate findet man aber in der Mitte der x-Werte von P1,P2.
============================
Wenn wir die blaue Gerade als Geschwindigkeits-Zeit Kurve auffassen, so ist die rote Kurve der Weg als Funktion der Zeit.
Die Geschwindigkeit steigt von einem Wert f'(4) bis f'(12) linear an.
Der zurückgelegte Weg steigt quadratisch mit der Zeit.
Der gleiche Weg mit konstanter Geschwindigkeit zurückgelegt, entspricht der Geraden P1-P2, die dazugehörige "mittlere Geschwindigkeit" ist jene Ordinate der blauen Geraden, die genau in der Mitte zwischen x=4 und x=12 liegt.
Die Parabel muss für dieses x ebenfalls diese (mittlere) Steigung haben.
=====================
Ich geb zu: meine Argumentation ist mit viel "Hausverstand" gemacht, Mathematiker suchen vielleicht Abstrakteres.
Gruß, Fern |
|