| Autor |
Beitrag |
    
anke

| | Veröffentlicht am Dienstag, den 05. Februar, 2002 - 13:07: | 
|
Kann mir irgendwer mithilfe des Differenzenquotienten (mit x und x0), wie man bei der Sinus- und Cosinusfunktion auf f'(x) kommt?
Vielen Dank im voraus! |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Mittwoch, den 06. Februar, 2002 - 11:32: | 
|
tja, da muesste ich schon voraussetzen,
dass Du wenigstens einsehen kannst dass
limX->0(sinX) / X = 1 ist; es zu beweisen ist etwas aufwendig wenn man nicht bereits die hier gesuchte Ableitung kennt und die L'Hospitalsche
Regel.
Aber "anschaulich" einsehbar ist es ja, dass für sehr kleine X gilt sinX ungefähr = X und die Tangente in X=0 sinX sehr gut nähert.
(sin(x+h) - sin(x))/h = 2*sin[(x+h-x)/2]*cos[(x+h+x)/2] / h
=
2*sin(h/2)*cos(x+h) / h = DifferenzenQuotient.
f'(sin(x)) wird daraus nun wenn h ->0 geht; und
wenn
man nun wie einleitend gesagt hinnimmt dass
limX->0sinX / X = 1 gilt und sinX = X für kleine X,
wird
daraus (sin x)' = cos x;
Die
Ableitung für cos x ist dann (sin(pi/2 - x))' |
    
anke

| | Veröffentlicht am Mittwoch, den 06. Februar, 2002 - 16:18: | 
|
Kannst du das vielleicht noch mal ohne h und mit x und x0 erklären? Also
(sin x - sin x0) /( x - x0)
Könnte eine Lehrerin so etwas in einer Klausur in der 11. Klasse drannehmen, wenn man es vorher nicht besprochen hat? |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Mittwoch, den 06. Februar, 2002 - 22:57: | 
|
Kann ich eigentlich nicht. Da unten würde ich auch wieder am liebsten x = x0+h substituiern.
In einer Klausur? - Das wär' ein "Genietest".
Na ja, vielleicht für "Zusatzpunkte", ausser Konkurenz.
(sin x - sin x0) / (x - x0) = 2*sin[(x - x0)/2]*cos[(x+x0)/2] /(x - x0)
nun, wenn x -> x0 wird sin[(x - x0)/2] immer genauer durch (x-x0)/2 angenähert, es bleibt also
schliesslich
2*0.5*(x-x0)*cos[(x+x0)/2]/(x-x0)= cos[(x+x0)/2]
was
für x->x0 zu cos x wird; aber für mich ist das eigentlich UNBEFRIEDIGEND.
Daher
das Folgende.(ich schreibe U für unendlich)
Zunächst:
ein Ausdruck "0/0" kann auch "0/(1/U)" = U*0 geschrieben werden.
In dem Buch "TRIUMPFE DER MATHEMATIK" von Heinrich Dörrie
fand ich nun den Nachweis das
limn ->Un*sin(w/n) = w was umgeformt
limn ->Usin(w/n) = w/n
limx ->0sin x = x
limx ->0 (sin x)/x = 1 ergibt.
(0)
Als bekannt vorausgesetzt wird dass für kleine x
(z.B. x < pi/4 = 45°) sin x < x < tan x gilt.
[zeichne in einen "Einheitkreis", einen kleinen Winkel x, sin x, tan x ein dann siehst Du es
]
Nun
Aus dem Buch
----------------------
Es ist
sin w = 2*sinw/2cosw/2
sin w = 2*tanw/2cos²w/2=2tanw/2(1-sin²w/2).
Wegen (0)
folgt sin w > 2*w/2*(1-w²/4)
oder sin w > w - w³/4.
Mithin
liegt sinw/n zwischen w/n und w/n - w³/(4n³),
d.h.
n*sinw/n zwischen w und w - w³/(4n²).
Also
ist limn ->Un*sinw/n = w
-------------
Ich werde auch noch eine geometrisch orientierte Herleitung bringen, aber heute nicht
mehr. |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Donnerstag, den 07. Februar, 2002 - 19:54: | 
|
lim(x->0)sin x/x HEUREKA!
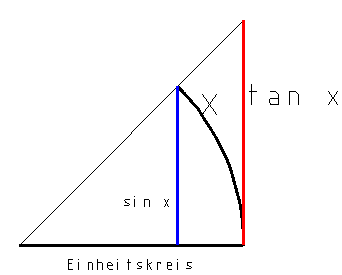
im Bild sieht man eindeutig wie schon erwähnt
sin x < x < tan x
1 < x/sin x < tan x/sin x
1 < x/sin x < sin x / cos x/sin x
1 < x/sin x < 1/cos x ; für die Reziprokwerte wird aus "<" ein ">"
1 > sin x/x > cos x; für x->0 schliesslich
1 > limx->0sin x/x > 1
also
kann der Grenzwert nur 1 sein.
Da-
mit gibt es bei den 1ten 2 Postings zu (sin x)'
kein Wenn und Aber mehr.
(noch geometrischer dann morgen) |
    
Martin (Martin243)

| | Veröffentlicht am Freitag, den 08. Februar, 2002 - 17:52: | 
|
Vorsicht:
Die Aussage
1 > limx®0 sin x/x > 1
ist natürlich falsch, es müsste
1 ³ limx®0 sin x/x ³ 1
heißen! |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Samstag, den 09. Februar, 2002 - 13:40: | 
|
sin'(x) GEOMETRISCH
Martin hat natürlich recht die Relationen sind
">="; aber in einem "Christian Tönnies" aus dem Jahre 1962, wo ich die Herleitung nun auch fand, stehen auch nur ">")
hier nun eine 1te geometrische Herleitung von
sin'(x) = cos(x)
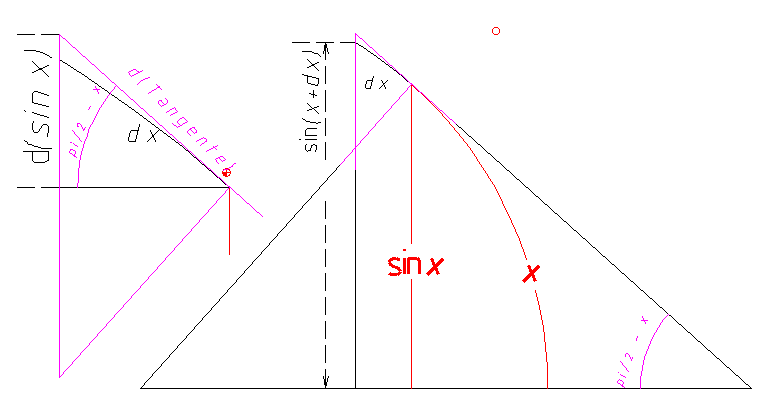
das linke vilolette Bild ist eine Auschnittvegrösserung des oberen rechten violetten Teils.
Man sieht dass
für dx -> 0 gilt dx -> d(Tangente)
also
d(sin x)/dx -> d(sin x)/d(Tangente) = sin(pi/2 - x) = cos x |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Donnerstag, den 14. Februar, 2002 - 13:31: | 
|
tgnte an sinus, darst.Geometrie
Da der Beginn des Threads wohl jenseits des oberen Bilschirmrands liegt, wiederhole ich sinngemäss ankes Frage:
lässt
sich (sin x)' = cos x denn irgenwie herleiten.
Hier durch Konstruktion der Tangente an die Sinuslinie mittels darstellender Geometrie und Analyse der Konstruktion.
Ich
behauptet hier nicht, die Konstruktion sei exakt mir Zirkel und Lineal möglich,
denn
r*pi lässt sich nicht konstruieren, die Zeichnung ist eben so genau wie möglich, durch Eingabe der Masszahl in das CAD-Progamm mit dem die Zeichnung entstand - aber man kann sich das ganze konstruiert vorstellen.
Verstehen muss man dabei dass
1)
die Tangente an die Raumkurve s, die aus der auf dem entrolltem Zylindermantel grün gestrichelten Linie entsteht
wenn
der Mantel auf/um den Zylinder gerollt wird,
mit
der Zylinderbasisebene immer denselben Winkel bildet wie die Linie vor dem Rollen.
Man
stelle sich das als Grenzprozess vor: der Mantel wird erst nur zu einem regulärem, z.B. 6seitigem Prisma gefaltet,
dann
zu einem 12seitigem u.s.w., bis er in einen Zylinder übergeht.
2)
das "Aufrissbild" (Projektion auf eine Ebene parallel zur Zyl. Achse) der s eine Sinuslinie ist
3)
und wie man das "Aufrissbild" der Tangente an die s konstruiert - das dann Tangente an eine Sinuslinie ist.

zu 2)
So wurde die angebliche Sinusline im Aufrissbild konstruiert :
zu jedem Winkelteilstrich (3° Abstand) auf dem Grundriss(halb)kreis wurde eine Senkrechte (punktiert) gezeichnet
zum
entsprechendem vertikalem Teilstrich eine Waagrechte, der Schnittpunkt markiert
und
die Punkte miteinander verbunden.
Beispiel Punkt P:
im
Grunriss bildet der gepunktete schwarze Radius mit dem roten Radius den Winklel x = 47*3° = (47/60)pi,
die
senkrechte blaue Strecke ist (47/60)*(r*pi) also = x wenn r = 1
und
aus dem Grundriss sieht man dass y = sin x
zu 3)
a)
die "x-Abstände", im Aufriss, von Punkten auf g, BLEIBEN UNVERVÄNDERT, wenn der Mantel um den Zylinder gekrümmt oder gerollt wird
b)
Die Raumkurve s kann mann sich aber auch so entstanden denken:
man
KRÜMME den Mantel NICHT, sondern rolle seine Ebene entlang des Zylinders.
Die
Punkte A°,B° der Basiskante wandern dann im Grundrissbild nach A',B' ; im Aufriss A",B",
die
"abgerollte" Strecke enstrpicht wieder dem gerolltem Winkel x,
und
die Punkte P sind die Schnittpunkte der Mantellinien entlang derer die "rollende Mantelebenene" den Zyl. gerade berührt
mit
der Geraden g auf der Mantelebene.
Wieder
ist die g in der rollenden Mantelebene Tangente an die Raumkurve s und das Aufrissbild von g die Tangente
an
das Bild der Kurve, also an die Sinuslinie. Die Verbindung von 2 Aufrisspunkten (A'',P) der gerollten g ist also die Tangente.
Und
aus dem Bild lässt sich ablesen dass für die Neigung der Tangente, damit also (sin x)' gilt
(sin x)' = -(x*cos(pi-x)) / x = cos x |
    
Friedrich Laher (Friedrichlaher)

| | Veröffentlicht am Freitag, den 15. Februar, 2002 - 19:07: | 
|
Bild also extra 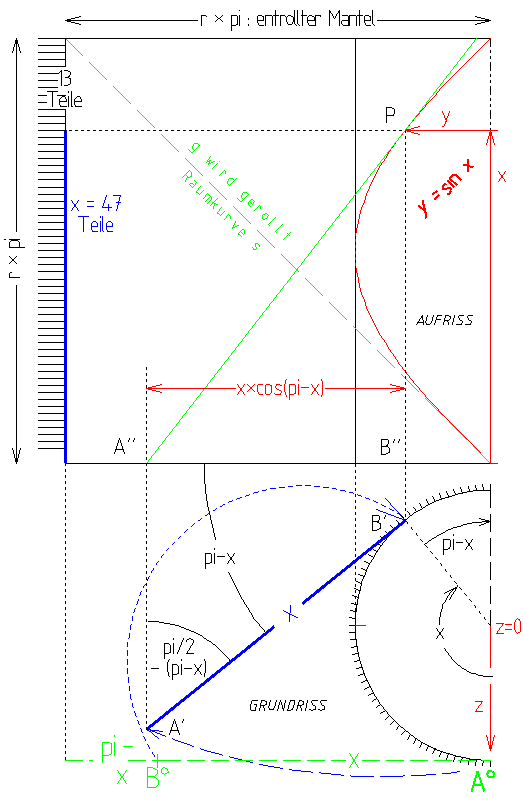 |
|