| Autor |
Beitrag |
    
Kati19

| | Veröffentlicht am Dienstag, den 14. März, 2000 - 13:43: | 
|
X^4-4t^2x^2-5t^2
1. Berechne Nullstellen, Extrema und Wendepunkte
2. Zeichne den Graphen für t=1
3. Wie groß ist die Fläche die von Graph und der x-Achse eingeschlossen wird?
Bitte ausführlich mit Lösungsweg. Danke meine Engel!!!! |
    
Pi*Daumen

| | Veröffentlicht am Mittwoch, den 15. März, 2000 - 17:51: | 
|
1)
f(x)=x4-4t²x²-5t²
Nullstellen:
Für Nullstellen substituiere z=x²
=> f(x)=z²-4t²z-5t²=0 <=> z=2t²±Ö(4t4+5t²) => x=±Ö[2t²±Ö(4t4+5t²)], was je nach t eigentlich bis zu 4 verschiedene Nullstellen liefern könnte, bei t=1 sind es z.B. 2 Nullstellen. Bei genauerem Betrachten sieht man aber, daß das zweite "-" nie zur Anwendug kommt, also weggelassen werden kann. Sonst wäre die Diskriminante der 1. Wurzel (das ist das unter der Wurzel) nämlich negativ. ALso immer 2 Lösungen.
Extremwerte:
f'(x)=4x³-8t²x=0 <=> x=0 oder x²=2t² <=> x=0 oder x=Ö(2)*t oder x=-Ö(2)*t
Setze die drei x-Werte in die 2. Ableitung f''(x)=12x²-8t² ein, um zu prüfen, ob es sich tatsächlich um Extremwerte handelt und ob Minimum oder Maximum.
Wendepunkte:
f''(x)=12x²-8t²=0 <=> x²=(2/3)t² <=> x=±tÖ(2/3)
Einsetzen in die 3. Ableitung zum Check.
2)
t=1
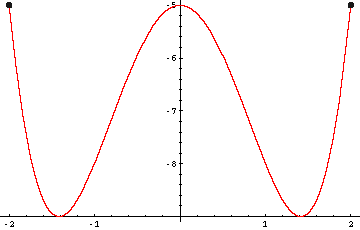
3)
Berechne einfach òf(x)dx und zwar mit den Grenzen Nullstelle1 und Nullstelle2.
Ich gehe davon aus, daß Du weißt, wie man die Stammfunktion eines Polynomes findet.
Wenn Du nicht sicher bist, melde Dich wieder.
Pi*Daumen |
|