| Autor |
Beitrag |
    
MATTHES

| | Veröffentlicht am Mittwoch, den 14. November, 2001 - 15:16: | 
|
Aus einer rechteckigen Fensterscheibe mit den Seitenlängen a und b ist vom Mittelpunkt der kleineren Seite aus eine Ecke unter einem Winkel von 45° abgesprungen. aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große neue Scheibe hergestellt werden. Wie sind die Maße der neuen Scheibe zu wählen?
BITTE WIRKLICH UM EINE SEHR GUTE ERKLÄRUNG dieser Aufgabe, ansonsten gebe ich echt auf, sitze schon sehr lange dran und entweder ich mache es mir zu schwer oder irgendetwas läuft hier falsch, denn ich verstehe sie wirklich nicht.
danke im voraus
MFG |
    
Kurz

| | Veröffentlicht am Mittwoch, den 14. November, 2001 - 17:46: | 
|
Hallo MATHES,
Das ist aber ein schöner kurzer Titel! |
    
Justin

| | Veröffentlicht am Donnerstag, den 15. November, 2001 - 12:33: | 
|
Hallo Mathes,
die Antwort lautet: soll die größte Fläche erzielt werden, muss die neue Scheibe der Quadratform MÖGLICHST NAHE kommen.
Das heißt konkret, dass die neue Scheibe so geschnitten werden muss, dass die kürzere Seite in voller Länge erhalten bleibt. Daraus ergibt sich dann die Länge der längeren Seite.
Warum?
Nun, es ist ein fester Umfang eines Rechteckes vorgegeben und daraus soll die größtmögliche Fläche erstellt werden.
u = 2a + 2b
A = a * b
b = (u-2a)/2 = u/2 - a
A = a * (u/2 - a) = a*u/2 - a²
=> Ableitung nach a
A' = u/2 - 2a
A'' = -2 => Extremum ist ein lokales Maximum
0 = u/2 - 2a
2a = u/2
=> 2b = u/2
=> a = b
=> Quadratform
Um es mit Worten auszudrücken:
Da die Seite a ein Viertel des Umfangs ausmachen muss, um eine größtmögliche Fläche zu erzielen, muss die Seite b ebenfalls ein Viertel des Umfangs umfassen. Demzufolge sind a und b gleich lang, was der Quadratform entspricht. |
    
Rudolf (Ruedi)

| | Veröffentlicht am Donnerstag, den 15. November, 2001 - 14:06: | 
|
Hallo Justin
Ist mir nicht ganz klar, weshalb die Scheibe möglichst in Quadratform gebracht werden muss, um die grösstmögliche Fläche zu erzeugen. Wenn der Umfang doch gegeben ist, ist doch auch die Fläche gegeben. 2a+2b=U und a*b=A. Die as und die bs sind jeweils dieselben. 4m*4m sind auch 16m2, wie 2m*8m.
Die Aufgabe ist, aus dem Rest der Scheibe eine möglichst grosse rechteckige Scheibe zu machen.
Wenn aus der Mitte der kürzeren Seite, nennen wir sie b, mit dem Winkel von 45° eine Ecke abgesprungen ist, dann wird b durch zwei geteilt, nennen wir die Hälfte x, dann ist 2x = b. Der einen Länge fehlt dann automatisch auch die Länge von x, weil die Ecke ein gleichschenkliges Dreieck darstellt bei dem x die beiden Schenkel sind.
Ich denke, wenn man an der Bruchstelle an der Länge die Scheibe zerteilt, ist die grösstmögliche Fläche aus dem Rest gewonnen. Die Breite bleibt b und die Länge ist a-x. Das Verhältnis der Seiten stimmt dann zwar nicht mehr überein mit dem ursprünglichem Längen-Breiten-Verhältnis, aber das ist ja auch nicht gefordert.
Die Fläche ist somit
A = (a-x)*b oder da x = b/2 ist (a-b/2)*b.
Gruss Rudolf |
    
Justin

| | Veröffentlicht am Donnerstag, den 15. November, 2001 - 15:14: | 
|
Hallo Rudolf,
jetzt rechne dein oben genannten Beispiel nochmal ganz genau nach :-)
Ein Quadrat von 4m * 4m hat 16m² Fläche und 16m Umfang.
Ein Rechteckt mit 2m * 8m hat zwar auch 16m² Fläche, aber einen Umfang von 20 m
Stimmt's oder hab ich recht?
Und mal folgendes Beispiel:
Die Scheibe hätte die Maße 6m * 4m gehabt.
Dann brach dieses eine Stück in Form eines Dreiecks heraus im Winkel von 45°, und zwar genau auf der Hälfte der kleineres Strecke.
Die Katheten des Dreiecks sind jeweils 2m lang.
Dadurch reduziert sich das nun die brauchbare Fläche der alten Scheibe auf 6m * 2m oder aber
auf 4m * 4m.
6m + 6m + 2m + 2m = 16m Umfang
4m + 4m + 4m + 4m = 16m Umfang
ABER:
6m * 2m = 12m²
4m * 4m = 16m²
Gleicher Umfang bei Rechtecken bedeutet als nicht unbedingt auch gleichen Flächeninhalt :-) |
    
Craig

| | Veröffentlicht am Donnerstag, den 15. November, 2001 - 23:23: | 
|
Hallo Ihr,
Ich glaube, die Schwierigkeiten für MATTHES sind in der Einordnung der Aufgabe zu suchen, ich finde, es ist weniger eine reine Extremwertaufgabe als viel mehr eine Aufgabe, die etwas mit einer Zuordnung nach Fallunterscheidung zu tun hat.
Es sind keinerlei Angaben über das Verhältnis Abmessungen a und b gemacht worden, und gerade das scheint eine zu bewältigende Schwierigkeit zu sein.
Ich stimme Justin zu, wenn er sagt: "soll die größte Fläche erzielt werden, muss die neue Scheibe der Quadratform MÖGLICHST NAHE kommen."
Die kürzere Seite muss in voller Länge erhalten bleiben, denn dann
nähern sich beide Seiten ziemlich an, also nahe an der Quadratform.
Mit der Aussage "Gleicher Umfang bei Rechtecken bedeutet als nicht unbedingt auch gleichen Flächeninhalt" würde ich sogar noch weiter gehen und behaupten:
"Gleicher Umfang bei Rechtecken bedeutet, dass sie keinen gleichen Flächeninhalt haben, außer (und jetzt kommt die einzige Bedingung, unter der der Inhalt doch gleich ist, und die ist trivial): wenn sie kongruent sind" (stimmt das wohl oder findet jemand ein Gegenbeispiel?)
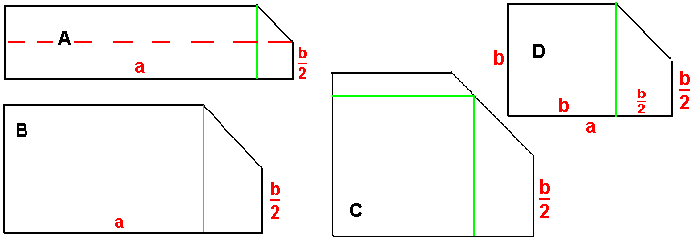
Jetzt kommt die Schwierigkeit:
Betrachte Scheibe B in der Abbildung.
Bei ihr ist a schon etwas kleiner als bei Scheibe A, b ist größer, aber trotzdem wird sie noch so geschnitten, dass die Länge der kürzeren Seite b vollständig erhalten bleibt.
Bei Scheibe C hingegen ist man schon innerhalb des Bereiches, der mit dem Aufgabenteil Extremwertberechnung zu tun hat. Hier muss vor dem Schnitt die genaue Größe des Quadrates bestimmt werden. (siehe später)
Irgendwo zwischen Fall B und Fall C muss die Grenze liegen, bei der man einerseits die kürzere Seite b vollständig ungekürzt lässt und gleichzeitig ein Quadrat herausschneidet.
Das ist dann der Fall, wenn die längere Seite auch auf Länge b zurückgeschnitten wird, also wenn die Kathete b/2 des Dreiecks zu b addiert genau a ergab:
a=3b/2
deshalb folgende Fallunterscheidung zur Festlegung, wie geschnitten werden muss:
die längere Seite habe Länge a, also b < a
0) ist a=3b/2, ist es egal, ob nach Anleitung von Fall 1) oder Fall 2) geschnitten wird.
1) ist 3b/2 < a, schneide bei x=b (Orientierung der x-Achsenrichtung siehe unten) parallel zur kürzeren Seite b, so dass die Seite vollständig erhalten bleibt.
2) ist a < 3b/2, schneide so, dass ein Quadrat entsteht, und zwar so:
Lege dazu ein Koordinatensystem auf die Scheibe, so dass die längere Seite a auf der x-Achse liegt und der Koordinatenursprung auf der Ecke der Scheibe liegt, die der Bruchstelle diagonal gegenüberliegt.
Der Graph der Funktion y=mx+n beschreibt dann die Bruchkante der abgesprungenen Ecke unter einem Winkel von 45°, 45° bedeutet, dass m=-1 ist (kann man auch etwas umständlicher aus zwei Punkten herleiten)
also gilt y=-x+n
Es muss y=b/2 gelten, wenn x=a gilt. Dies ist eine Bedingung zur Bestimmung von n:
b/2 = -a + n => n=b/2 +a
=>
y=-x +b/2 +a
Die Fläche A(x,y)=x*y der Restscheibe soll maximal werden.
Dazu setze y=-x +b/2 +a in A(x,y) ein und erhalte eine Funktion A(x):
A(x)= x*(-x +b/2 +a) = -x² +(b/2 +a)x
bilde Ableitungen:
A'(x) =-2x + b/2 +a
A''(x)= -2 <0 => auf jeden Fall nur Maximum
setze A'(x)=0 => -2x + b/2 +a = 0 => b/2 +a = 2x => x = b/4 + a/2
setze dies in y ein => y = -b/4 - a/2 + b/2 + a = b/4 + a/2
y muss ja auch denselben Wert haben wie x, wenn ein Quadrat entstehen soll.
Also muss die Scheibe so geschnitten werden, dass ein Quadrat der Seitenlänge b/4 + a/2 entsteht.
Ich denke, das war gefragt.
Zusatzbetrachtung:
Der Flächeninhalt dieses Quadrates ist A = (b/4 + a/2)² = b²/16 + ab/4 + a²/4
Dies stimmt für den Grenzfall a = 3b/2 zwischen den Fällen 1) und 2) überein:
A=(b/4 + 3b/2/2)²=(b/4 +3b/4)²=b², was ja auch entsteht, wenn man nach Fall 1) schneidet. |
    
Craig

| | Veröffentlicht am Donnerstag, den 15. November, 2001 - 23:33: | 
|
Vertan, bei Fall 1) muss es heißen:
1) ist 3b/2 < a, schneide bei x=a -b/2
(kürze die längere Seite von a auf a -b/2) |
|