| Autor |
Beitrag |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Dienstag, den 09. Oktober, 2001 - 22:08: | 
|
Man beweise:
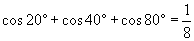
! |
    
Frederic

| | Veröffentlicht am Dienstag, den 09. Oktober, 2001 - 22:47: | 
|
Hallo Pascal,
Das kann man nicht beweisen, weil es nicht stimmt. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 09:10: | 
|
Welch ein Fehler, es muss heissen:
cos 20° * cos 40° * cos 80° = 1/8
Jetzt sollte es stimmen ! |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 12:12: | 
|
Hi Pascal,
Es ist für mich eine angenehme Pflicht,
Deine schöne Aufgabe zu lösen ,dies umso mehr,
als das vorausgehende Datum samt Uhrzeit,
nämlich 10.10. 2001,10 Uhr 10, mir ausnehmend gefällt.
Zur Lösung verwenden wir zweimal die aus dem
Additionstheorem des Cosinus stammende Formel:
cos u * cos v = ½ * [cos(u+v) + cos(u-v)] .
Damit erhalten wir zunächst :
A = cos 20° * cos 40°
= ½ * [cos(20°+40°) + cos(20°-40°)]
= ½ * [cos 60° + cos 20°] = ¼ + ½ * cos (20°)
Dies ist noch mit cos 80° zu multiplizieren
Schlusssresultat B = A* cos 80°:
= ¼ * cos 80° + ½ * cos 20° * cos 80°
= ¼ * cos 80° + ¼ * [cos (20°+80°) + cos(20°-80°)]
= ¼ * cos 80° + ¼* cos 100° + ¼ * cos60° =
= ¼ * cos 80° - ¼ * cos 80° + ¼ * cos 60° = 1/8
Beachte : cos(-20°) = cos 20°
cos 100° = - cos 80°
Mit freundlichen Grüßen
H.R.Moser,megamath. |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 12:33: | 
|
Hi Pascal,
Im Anschluss an die Lösung Deiner Aufgabe
schlage ich vor, die folgenden Beziehungen zu beweisen,
im Sinne einer nützlichen Uebung:
a) 8 * sin 20° * sin 40° * sin 80° = wurzel(3)
b) tan 20° * tan 40° * tan 60° * tan 80° = 3
c) tan 60° - tan 40° - tan 20° = tan 60° * tan40° * tan 20° .
Viel Vergnügen wünscht
H.R.Moser,megamath. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 16:53: | 
|
Hi H.R.Moser
Zu Aufgabe a)
Wegen
sin u * sin v = ½ * [cos(u-v) - cos(u+v)]
ist
sin 20° * sin 40° = ½ * cos 20° - ¼
Also ist
sin 20° * sin 40° * sin 80° = ½ * cos 20° * sin 80° - ¼ * sin 80°
= ¼ * (sin 60° + sin 100°) - ¼ * sin 80°
= ¼ * (Wurzel(3)/2 + sin 80°) - ¼ * sin 80°
= Wurzel(3)/8
Die andern beiden Aufgaben kann ich im Moment nicht bearbeiten, da ich keine geeigneten Produkt- und Summenformeln für den Tangens zur Hand habe.
Mit freundlichen Grüssen, P. Rolli
PS: Warum eigentlich 'megamath.' ? |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 17:03: | 
|
Soeben bin ich auf folgenden Zusammenhang gestossen, doch leider sind bisher alle Beweisversuche gescheitert.
Pi/4 = 5 * acot(7) + 2 * acot(79/3)
wobei mit acot die Umkerfunktion des Cotangens gemeint ist.
Gruss, Pascal |
    
Carmichael (Carmichael)

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 20:27: | 
|
Hi,
bekanntlich gilt ja:
cot(Phi) = 1/tan(Phi) := z;
=> Phi = atn(1/z); [ atn sei inverser tan)
^=> acot(z) = Phi = atn(1/z); (*)
Nun nehmen wir uns noch folgendes Additionstheorem zu Hilfe:
tan(u+v) = (tan(u) + tan(v)) / (1 - tan(u)*tan(v))
(siehe Formelsammlung)
dieses leicht umgeformt ergibt:
atn(tan(u)) + atn(tan(v)) = atn[ (tan(u) + tan(v)) / (1 - tan(u)*tan(v)) ] ;
wir setzen nun x := tan(u) und y := tan(v) und erhalten:
(1) atn(x) + atn(y) = atn( x+y / (1-xy) ) ;
Nun zurück zur Behauptung:
Pi/4 = 5 * acot(7) + 2 * acot(79/3)
Für den Beweis wenden wir einfach (*) und (1) ein paar mal an:
5 * acot(7) + 2 * acot(79/3) =
5 * atn(1/7) + 2 * atn(3/79) =
3 * atn(1/7) + 2 * (atn(1/7) + atn(3/79)) =
3 * atn(1/7) + 2 * (atn[ (1/7+3/79)/(1-3/(7*79)) ]) =
3 * atn(1/7) + 2 * atn(2/11) =
atn(1/7) + 2 * atn(1/3) =
atn(1/7) + atn(3/4) =
atn1 = Pi/4;
Gruss, Carmichael |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 10. Oktober, 2001 - 20:33: | 
|
Hi Pascal,
Bei der Lösung Deiner letzten Aufgabe betreffend arcctg
bin ich Dir gerne behilflich, damit Du Dich nicht an die
Freunde der Zahl Pi in Wien zu wenden brauchst,
allerdings unter der Voraussetzung ,dass ich eine neue
passende Aufgabe aus demselben Gebiet stellen darf.
Wir schreiben Deine Aufgabe um , indem wir arctan
einführen:
zu beweisen ist demnach:
5 * arctan (1 / 7 ) + 2 * arc tan ( 3 / 79) = ¼ * Pi
Sei arctan ( 1 / 7 ) = u , arctan ( 3 / 79 ) = v,
somit tan u = 1 / 7 , tan v = 3 / 79.
Mit Hilfe der Doppelwinkelformel des Tangens kommt:
tan ( 2 * u ) = (2 / 7 ) / [1 - 1 / 49 ] = 7 / 24.
Mit dem Additionstheorem des Tangens und
der Doppelwinkelformel des Tangens erhalten wir
der Reihe nach:
tan ( 2 * u + v ) = [7 / 24 + 3 / 79] / [ 1 - 7 / 632] = 1 / 3
tan ( 4 * u + 2 * v ) = tan { 2 * (2 * u + v )} =
= [2 / 3] / [ 1 - 1 / 9 ] = 3 / 4 .
also
tan ( 5 * u + 2 * v ) = tan [ (4 * u + 2 * v) + u ) =
= [3 / 4 + 1 / 7 ] / [1 - 3 / 28 ] = 1 ; BRAVO !
Uebergang beiderseits zur Arcustangens-Funktion:
führt auf
arc tan { tan (5*u +2*v) } = arctan 1 = Pi / 4
Links steht vereinfacht : 5 * u + 2 * v .
Damit ist wegen der Bedeutung von u und v
die Formel bewiesen, wenn man noch beachtet , dass
5 / 7 + 6 / 79 < 1 gilt.
Die angekündigte neue Aufgabe lautet.
Beweise:
½ * arctan 10 + ¼ * arcsin ( 20 / 101 ) = ¼ * Pi .
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Mit freundlichen Grüßen
H.R.Moser,megamath
P.S.
Zu deiner Frage unter P.S:
Bei der Suche nach einem Zerevis für meine Mitarbeit
bei "zahlreich" schlugen meine Fans die Namen
"gigamath" und " teramath " vor; bekannte Bezeichnungen für
grosse Dinge in der Physik ( Tera 10^12, Giga 10^9 )
Aus Bescheidenheit habe ich mich mit dem vorliegenden
vulgo begnügt .
Nochmals Gruss
Megamath. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Donnerstag, den 11. Oktober, 2001 - 11:03: | 
|
Hi H.R.Moser, examath (= 10^18)
Um die Aufgabe zu lösen, ziehe ich nebst der bereits genannten Doppelwinkel- und Summenformel noch die folgende heran:
tan (arcsin x) = x / Wurzel(1 - x^2)
Nach Multiplikation mit 4 lautet die Gleichung:
2 * arctan 10 + arcsin (20/101) = Pi
Sei u = arctan 10 und v = arcsin (20/101), dann muss gelten tan(2 * u + v) = 0 da tan Pi = 0
tan (2 * u) = 20 / (1 - 100) = -20/99
Von tan (2 * u + v) untersuche ich zunächst den Zähler:
Zähler = -20/99 + [(20/101) / Wurzel( 1 - (20/101)^2)]
= -20/99 + (20/101) / (99/101) = -20/99 + 20/99 = 0
Da nun der Zähler 0 ist nimmt der ganze Bruch den Wert 0 an und die Berechnung des Nenners erübrigt sich.
Damit sollte, wenn ich mich nicht verrechnet habe der Beweis erbracht sein.
Mich würde (wenn wir gerade am Aufgaben stellen sind) noch folgendes interessieren:
- Wie lassen sich Gleichungen dieser Art generieren ?
- Wie beweist man die von mir oben eingeführte Formel ?
Mit freundlichen Grüssen, Pascal
PS: Betreiben Sie Mathematik als Hobby oder als Beruf (oder beides) ? |
    
N.

| | Veröffentlicht am Donnerstag, den 11. Oktober, 2001 - 16:59: | 
|
Hallo Pascal,
wenn ich mich auch nochmal beteiligen dürfte....
Zum Beweis deiner Formel:
tan(y)=sin(y)/cos(y)=sin(y)/Ö1-sin²y
für y=arcsin(x) folgt:
tan(arcsin(x))=x/Ö1-x²
=====================================
q.e.d. |
    
N.

| | Veröffentlicht am Donnerstag, den 11. Oktober, 2001 - 17:16: | 
|
Ach so,
eine Aufgabe hätte ich da auch noch-Wie megamath sagen würde....
Man beweis:
cos20°+cos60°+cos100°+cos140°=1/2
viel vergnügen...
Gruß N. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Donnerstag, den 11. Oktober, 2001 - 22:21: | 
|
Hi N.
Zu deiner Aufgabe:
cos 20° + cos 60° + cos 100° + cos 140° = 1/2
vereinfacht sich wegen cos 60° = 1/2 zu:
cos 20° + cos 100° + cos 140° = 0
cos 20° + cos (120° - 20°) + cos(120° + 20°) = 0
nach dem Additionstheorem folgt:
cos 20°
+ (cos 120° * cos 20° + sin 120° * sin 20°)
+ (cos 120° * cos 20° - sin 120° * sin 20°) = 0
oder vereinfacht:
cos 20° + 2 * cos 20° * cos 120° = 0
da cos 120° = -1/2:
cos 20° - cos 20° = 0
Also ist die Gleichung korrekt !
Gruss, Pascal |
    
Pascal (Prolli)

| | Veröffentlicht am Donnerstag, den 11. Oktober, 2001 - 23:16: | 
|
Hallo allerseits !
Soeben ist es mir gelungen, die folgende Gleichung herzuleiten:
cos 1° + cos 62° + cos 119° = cos 2° + cos 59° + cos 122°
Wer kann das beweisen ?
Gruss, Pascal |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 12. Oktober, 2001 - 08:37: | 
|
Hi Pascal
Zunächst soll die Aufgabe von "N" gelöst werden.
Vielleicht kann die hier zur Lösung eingesetzte Methode
auch für Deine neueste Aufgabe dienstbar gemacht werden.
Als Grundlage dient die Relation
cos u - cos v = - 2 * sin [½ (u+v)] * sin [½ (u-v)].........(I)
Wir formen um:
S = cos20° + cos60° + cos100° + cos140° =
cos20° + cos60° - cos80° - cos40° =
cos20° - cos40° + cos60° - cos 80° =
cos20° - cos40° + ½ - sin10°
Nach (I) erhalten wir:
.S = - 2 * sin 30° * sin (-10°) + ½ - sin10° =
sin10° + ½ - sin10° = ½
Gruss
H.R.Moser,megamath (immer noch) |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 12. Oktober, 2001 - 10:31: | 
|
Hi Pascal,
Wie man in spielerischer Tätigkeit mit Formeln der Goniometrie
auf verschlungenen Pfaden zu einem Ziel kommen kann,
zeigt die folgende kleine Rechnung (Blick hinter die Kulissen !).
Sei T = tan x.
Wir wollen U = tan 2x und V= tan 3x durch T ausdrücken.
Wir erhalten mit den bekannten Formeln:
U = 2 * T / [1 - T ^ 2 ] und nach einiger Rechnung
V = T * [ 3 - T ^ 2 ] / [1 - 3 * T ^2 ]
Nun bilden wir das Produkt
P = T * U * V ; eine vereinfachte Form für P lautet:
P = 2 * T ^ 3 * [ 3 - T ^2 ] / [(1 - T ^ 2 ) * ( 1 - 3 * T ^ 2 )]
Für die Differenz D = tan x* tan 2x * tan 3x - tan 3x = P - V
erhalten wir:
D = T * [ 3 * T ^ 4 - 10 * T ^2 + 3 ] / [(1-T^2)*(3T^2-1)]
Das Polynom vierten Grades in T in der ersten eckigen Klammer
enthält den Faktor (3 * T ^ 2 - 1 ) , der auch im Nenner steht
und somit weggekürzt werden kann.
Wir erhalten für D den Term:
D = T * ( T ^ 2 - 3 ) / ( 1 - T ^2 );
Andrerseits gilt für die Summe S von T und U :
S = T + U = T * (3 - T ^2 ) / (1 - T ^ 2 )
Daraus entspringt das Schlussresultat:
D = - S oder P - V + S = 0, ohne Hieroglyphen:
tan x * tan 2x * tan 3x - tan 3x + tan x + tan 2x = 0
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Ersetzt man in dieser Relation x durch 20°, so erhält man das
Resultat zu meiner Aufgabe c) vom 10.10. 20001,13 Uhr 33,
welche damit auf Umwegen gelöst wurde.
Mitfreundlichen Grüssen
H.R.Moser,megamath. |
    
N.

| | Veröffentlicht am Freitag, den 12. Oktober, 2001 - 19:03: | 
|
Hallo Pascal,
durch das lösen der von mir gestellten Aufgabe hast du praktisch die Aufgabe, die du am anfang dieser Diskussion gestellt hast selbst gelöst.
Ürsprünglich war ja zu beweisen:
cos 20° * cos 40° * cos 80° = 1/8
Und für die Multiplikation dreier Cosinusterme gibt es ja eine Fertigformel die ich dir gerne bei bedarf herleite-fals du es nicht selber schaaffen soltest-
Sie Lautet:
cos(a)*cos(b)*cos(c)=1/4*[cos(a+b-c)+cos(b+c-a)+cos(c+a-b)+cos(a+b+c)]
naja, und den Rest kennst du ja schon....
Gruß N. |
|