| Autor |
Beitrag |
    
Jörg Lauf (hohescorange)

Neues Mitglied
Benutzername: hohescorange
Nummer des Beitrags: 1
Registriert: 12-2002
| | Veröffentlicht am Montag, den 09. Dezember, 2002 - 22:59: | 
|
hallo,
ich würde gerne wissen welche schritte zu der lösung führten:
(a^3+b^3)/(a^3+(a-b)^3)= ? =
(a+b)/(a+(a-b))
könntet ihr bitte mir auch die schritte erklären und beim namen nennen?
gibt es noch weiterer solcher regeln, oder zumindest eine online quelle wo ich soetwas selbst nachlesen könnte?
vielen vielen dank |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 754
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 10. Dezember, 2002 - 09:38: | 
|
Sowohl Zähler als auch Nenner lassen sich
nach der Formel (x³+y³)=(x+y)(x²-xy+y²) Zerlegen
(a³+b³)=(a+b)(a²-ab+b²)
[a³+(a-b)³]=[a+(a-b)][a²-a(a-b)+(a-b)²]
im 2ten Faktor nach (a-b) zusammenfassen
[a³+(a-b)³]=[a+(a-b)][a²-(a-b)(a-(a-b))]
[a³+(a-b)³]=[a+(a-b)][a²-(a-b)b]
[a³+(a-b)³]=[a+(a-b)](a²-ab+b²)
also| | | Zähler | = | (a²-ab+b²)(a+b) | | Nenner | = | (a²-ab+b²)[a+(a-b)] |
(Beitrag nachträglich am 10., Dezember. 2002 von friedrichlaher editiert)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Tilo (schubtil)

Neues Mitglied
Benutzername: schubtil
Nummer des Beitrags: 3
Registriert: 12-2002
| | Veröffentlicht am Dienstag, den 10. Dezember, 2002 - 14:01: | 
|
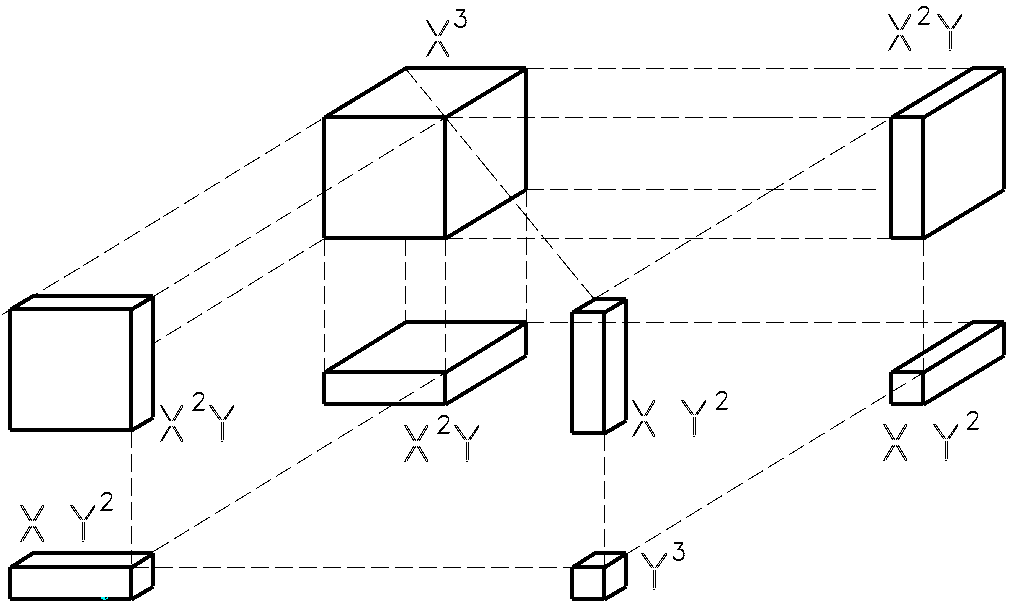
Jörg hatte noch nach eine Quelle für die Regel gesucht. Ich auch, habe aber mit google unter binomische bzw. trinomische? Formel nichts für die 3.Potenz gefunden. Deshalb habe ich mir einen Würfel aufgemalt und dort Quader mit der Kantenlängen a und b hineingezeichnet. Man kommt dadurch auf die gleiche Formel:
x³+y³=(x+y)(x²-xy+y²)
Diese entsteht durch umformen aus den einzelnen Volumengleichungen der Quader und Würfel im großen Würfel:
x³+3x²y+3xy²+y³=(x+y)³
x³+y³=(x+y)³-3x²y-3xy²
usw...
Allerdings hatte ich anschließend Kopfschmerzen, weil es doch extrem anstrengend war, mir den Würfel mit den verschiedenen Quadern und Würfeln vorzustellen.
Evtl kennt Friedrich noch eine Quelle im Internet. Ich schau heute Abend noch mal in meinen alten Göhler.
Die weitere Lösung kann ich mir jetzt schenken, bei Friedrich ist nichts hinzuzufügen.
(Beitrag nachträglich am 10., Dezember. 2002 von schubtil editiert)
(Beitrag nachträglich am 10., Dezember. 2002 von schubtil editiert) |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 755
Registriert: 02-2002
| | Veröffentlicht am Dienstag, den 10. Dezember, 2002 - 17:36: | 
|
Du beschämst mich, Tilo. Ich bin sonst auch sehr für Anschauung.
Wenn Du tatsächlich über eine Zeichnung zu (x+y)³ = ... gekommen bist, ALLE ACHTUNG !
Allerdings
bereitet da Algebra, glaube ich, weniger Kopfweh,
und
führt auch zu Deiner 2ten Zeile.
Und
die Formel
x³+y³ = (x+y)(x²-xy+y²)
ist
ja nur ein Sonderfall der
allgemeinen
xn+yn = (x+y)(xn-1-xn-2y+xn-3y2-..)
für ungegrade n
und
xn-yn = (x-y)(xn-1+xn-2y+xn-3y2..)
für
gerade. und bei n > 3 hilft Anschauung kaum mehr.
Zu
meiner Schulzeit wurde sie uns
einfach bekannt gemacht und zum Beweis überlassen.
Man
kann sich aber auch überlegen
was
die Polynomdivisionen (xn±yn) : (x±y)
ergeben,
unter welchen Bedingungen sie "aufgehen".
Schließlich
hätte man im Unterricht auch schon
bei
der Behandlung der geometrischen Reihe
auf
diese Formeln hinarbeiten können,
denn
die langen Klammerausdrücke sind eine,
mit
dem Faktor ±y/x .
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Tilo (schubtil)

Neues Mitglied
Benutzername: schubtil
Nummer des Beitrags: 5
Registriert: 12-2002
| | Veröffentlicht am Mittwoch, den 11. Dezember, 2002 - 07:15: | 
|
Noch ein letztes Mal zu dieser Angelegenheit.
Danke an Friedrich für die Gleichung, kann ich gelegentlich brauchen. Ich musste wegen fehlender Errinnerung an solche allgemeinen Formeln tatsächlich den Würfel zeichnen um die Gleichung zu finden. Mein letztes Mathe ist so 8-9 Jahre zurück. Jetzt habe ich festgestellt viel vergessen zu haben. Deshalb versuche ich mich an diesen Aufgaben hier.
Vor kurzem habe ich auch mal eine frühere Prüfungsaufgabe von mir gerechnet: Den Rauminhalt einer Mensch-Ärgere-Dich-Nicht-Figur. Mit einem Freund zusammen haben wir es noch hinbekommen, allerdings hat es den ganzen Tag gedauert.
Falls ich also mal was falsches hier schreibe, bitte ich um Berichtigung, ich bin "wiederlernend".
Gruß
Tilo
|
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 759
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 12. Dezember, 2002 - 14:42: | 
|
um künftiges Kopfweh zu vermeiden
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
|