| Autor |
Beitrag |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Samstag, den 23. Juni, 2001 - 12:35: | 
|
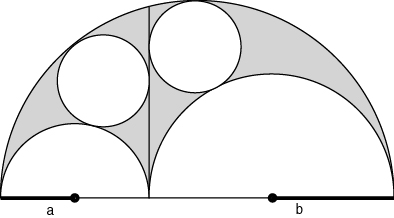
Archimedes hat gezeigt, dass die zwei Inkreise in den beiden Teilen des "Schustermessers" gleich gross sind. Wie gross ist ihr Radius ? |
    
Sandra

| | Veröffentlicht am Sonntag, den 24. Juni, 2001 - 16:31: | 
|
a und b sind beliebig wählbar? |
    
Sandra

| | Veröffentlicht am Sonntag, den 24. Juni, 2001 - 16:36: | 
|
Habe eine andere Version (verständlicher, aber nicht unbedingt gleich ??) gefunden:
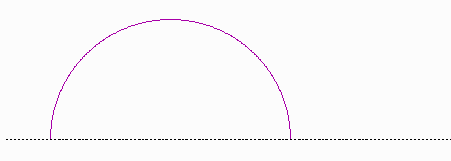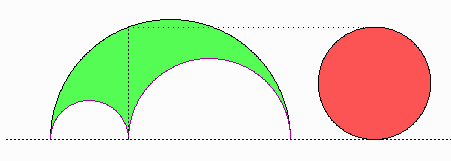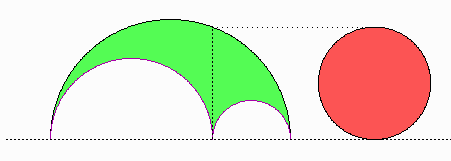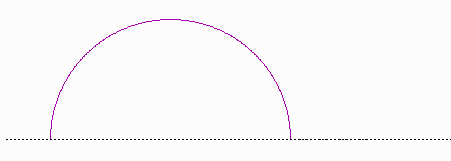
Warum ist der rote Kreis stets flächengleich zu dem grünen "Schustermesser" (des Archimedes)? |
    
Sandra

| | Veröffentlicht am Sonntag, den 24. Juni, 2001 - 16:40: | 
|
Das habe ich bei der TU-Freiberg gefunden:
Quote:Archimedes gab den Flächeninhalt F der folgenden Figur an, die er Arbelos ("Schustermesser") nannte. Sie wird heute auch als Möndchen oder (Mond-)Sichel des Archimedes bezeichnet.
Eine Strecke c = AB werde durch einen Punkt D in zwei Teile p = AD und q = DB geteilt. Das Lot in D auf AB schneide den Halbkreis über AB in C. Es sei h = CD die Höhe im rechtwinkligen Dreieck ABC. Zieht man von der Fläche des Halbkreises über AB die Fläche der beiden Halbkreise über AD und DB ab, so entsteht der Arbelos. Es ist daher
F = pi/8*c*c - pi/8*p*p - pi/8*q*q
= pi/8*((p+q)*(p+q) - p*p - q*q)
= pi/8*(2*p*q) = pi/4*p*q = pi/4*h*h,
wobei zuletzt der Höhensatz h*h = p*q im rechtwinkligen Dreieck verwendet wurde. Also ist F gerade der Flächeninhalt des Kreises mit dem Durchmesser h = CD.
|
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Montag, den 25. Juni, 2001 - 16:18: | 
|
Hallo Sandra !
Das war mir schon bekannt, denn in deinem Text geht es um die grüne Fläche. Mich interessiert aber der Radius der beiden Inkreise ! |
    
H.R.Moser,megamath.

| | Veröffentlicht am Montag, den 25. Juni, 2001 - 21:20: | 
|
Hi Pascal,
Die Bezeichnungen, die wir bei der Lösung
Deiner Aufgabe verwenden wollen, seien die
folgenden :
Mittelpunkt M des grossen Halbkreises M
Radius R , Durchmesser AB
Mittelpunkt des Halbkreises links: P auf AM , Radius a
Mittelpunkt des Halbkreises rechts Q auf MB ,Radius b
vertikale Halbsehne FH (F auf AM , H auf grossem Halbkreis)
Erster Berührungskreis k1 links, Mittelpunkt N1, Radius r1
Zweiter Berührungskreis k2 rechts, Mittelpunkt N2 Radius r2
Es wird Dir übrigens nicht schwer fallen,
dazu eine schöne Figur ins Board zu stellen.
Zu zeigen ist: r1 = r2
Lösungsidee
Wir berechnen zuerst r = r1 , ausgedrückt durch a , b
vertauschen dann a und b und erhalten r2
Es wird sich zeigen, dass der Ausdruck für r gegenüber
Dieser Vertauschung invariant ist .
Wir beschäftigen uns daher nur mit k1 .
Die Berührungspunkt von k1 mit dem kleinen Halbkreis
links sei U, derjenige mit der Strecke FH sei V und
derjenige mit dem Halbkreis , Durchmesser AB , sei W.
Vom Mittelpunkt N des Kreises k1 fällen wir das Lot auf
den Durchmesser AB ;G sei der Fusspunkt dieses Lotes auf AB.
Die Länge der Strecke NG werde mit h bezeichnet
Nun kann die Rechnung beginnen.
Radius R = a + b.
Im rechtwinkligen Dreieck NGM gilt:
Kathete NG = h , Kathete GM = r + FM = r + R - 2 a.
Hypotenuse MN = R - r
Nach Pythagoras gilt h ^ 2 = ( R - r )^2 - ( r + b - a ) ^ 2
Also h^2 = (R + b - a) * (R -2 r - b + a ) = 2 * b * 2 * ( a - r)
h^2= 4 b * ( a - r).....................................................................(1)
Im rechtwinkligen Dreieck NGP gilt:
Kathete NG = h, Kathete GP = a - r .
Hypotenuse NP = a + r , daraus nach Pythagoras:
h^2 = ( a + r) ^ 2 - ( a - r) ^ 2 = 2 * a * 2 * r = 4* a * r ..........(2)
Aus (1) und (2) folgt durch Gleichsetzung
a * b - r* b = a *r , daraus
r = a * b / ( a + b)
°°°°°°°°°°°°°°°°°°
Dieser Ausdruck ist tatsächlich invariant gegenüber der
Vertauschung von a und b in ihrer Rolle.
Damit ist der Beweis erfolgreich erledigt.
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Dienstag, den 26. Juni, 2001 - 18:13: | 
|
Danke für die schnelle Antwort !
Hier folgt die Fortsetzung der Aufgabe: (Für mich unlösbar...)
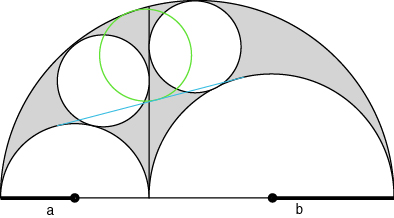
Man beweise, dass der grösste Kreis welcher den grossen Halbkreis und die Tangente der beiden kleineren Halbkreise berührt, den selben Radius hat wie die kleinen Kreise der vorherigen Aufgabe ! |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 27. Juni, 2001 - 09:15: | 
|
Hi Pascal,
Deine neue Aufgabe ist harmloser, als sie auf den
ersten Blick erscheint .
Ergebnis:
Der Durchmesser des gesuchten Kreises stimmt
mit dem Abstand zweier Tangenten t1 und t2 überein.
t1 ist die gemeinsame (äussere) Tangente der beiden
kleinen Halbkreise, t2 die dazu parallele Tangente
des grossen Halbkreises .
Wir zeigen :
d = 2 * a * b / ( a + b ) ,
°°°°°°°°°°°°°°°°°°°°°°
wobei ,wie in der letzten Arbeit, a der Radius des linken
Halbkreises (Mittelpunkt P), b der Radius des rechten
Halbkreises (Mittelpunkt Q) ist
R = a + b ist der Radius des grossen Halbkreises mit
Mittelpunkt M.
Weitere Bezeichnungen.
Der Berührungspunkt der Tangente t1 auf dem grossen
Halbkreis sei T.
Die Gerade n = MT steht auf t1 senkrecht ; n schneidet
auch t2 senkrecht; der Schnittpunkt sei E.
Durch den Mittelpunkt P des linken Halbkreises legen wir
die Parallele p zu t1 und t2 .
p schneidet n im Punkt C und die Parallele q durch Q zu n
im Punkt D.(Q ist der Mittelpunkt des Halbkreises rechts).
Bitte alles in der Figur eintragen !
Wir benötigen die Streckenlängen :
QD = b - a , wie man der Figur entnehmen kann; weiter:
PM = R - a = a + b - a = b und
PQ = a + b
Wir berechnen nun die Länge x der Strecke MC
Dies geschieht mit Hilfe des zweiten Strahlensatzes auf folgende
Art:
MC / QD = PM / PQ ,daraus
x = MC = PM / PQ * QD = b * ( b - a ) / ( a + b )..........................(1)
Auf der Normalen n lesen wir wie auf einem Präsentierteller ab
TE +EC + x = R ; setzen wir x aus (1) ein und lösen nach d auf ,
so kommt:
d = b - b * (b-a) / ( a + b ) = 2 * a * b / ( a + b ) = 2 * r,
(r aus der letzten Arbeit) , w.z.b.w.
Schlussfrage: Geht es von Dir aus in diesem Stil weiter ?
Mit freundlichen Grüssen
H.R.Moser ,megamath. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Mittwoch, den 27. Juni, 2001 - 16:51: | 
|
Und wieder einmal sage ich: Danke.
Aber: Einen hab' ich noch !
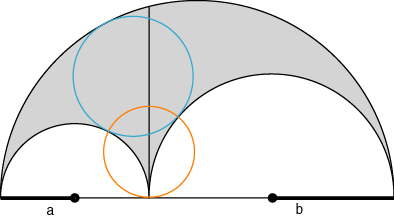
Der Kreis (orange) welcher durch die Berührungspunkte der beiden Halbkreise mit dem grössten einbeschriebenen Kreis (blau) und durch den Fusspunkt von h läuft hat - wie könnte es anders sein - den gleichen Radius/Durchmesser wie die vorherigen drei Kreise.
Zusatzfrage: Wohnen Sie in der Schweiz (wie ich) und welcher Ausbildung verdanken sie dieses Wissen ?
Gruss, Pascal |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 27. Juni, 2001 - 20:29: | 
|
Hi Pascal,
Es ist höchste Zeit , dass ich mich mit einer kleinen Aufgabe
revanchiere.
Derjenige Kreis, welcher den grossen Halbkreis und ausserdem
die Standlinie AB im Berührungspunkt F der beiden kleinen
Halbkreise berührt, hat den Radius - wie kann das anders sein -
2 * r = 2 * a b / ( a + b)
°°°°°°°°°°°°°°°°°°°°°°°
Man beweise diese Behauptung !
Mit freundlichen Grüssen
H.R.Moser,megamath. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Mittwoch, den 27. Juni, 2001 - 21:05: | 
|
Entschuldigen Sie, wenn ich ihre Revanche-Behauptung nicht beweisen kann, denn ich verstehe sie nicht: F ist Schnittpunkt der Halbsehne und dem Durchmesser des grössten Halbkreises ?
PS: Da es Ihnen ja nicht allzu schwer zu fallen scheint: beweisen sie noch meine letzte Behauptung ! (und beantworten Sie die Zusatzfrage !) |
    
H.R.Moser,megamath.

| | Veröffentlicht am Mittwoch, den 27. Juni, 2001 - 22:42: | 
|
Hi Pascal,
Meine Revanchegelüste waren natürlich nicht ernst gemeint.
Ich löse, wenn möglich, die vom mir gestellten Aufgaben
auch selbst, nur ist all dies eine Frage des Zeitaufwandes.
Nun zur Lösung Deiner dritten Aufgabe, die übrigens mit
meiner Aufgabe aufs engste verbunden ist, indem der
Mittelpunkt "meines" Kreises der höchste Punkt Z
"deines" dritten Kreises ist.
F ist nach wie vor der Berührungspunkt der beiden kleinen
Halbkreise und liegt auf dem Durchmesser AB des grossen .
Der genannte Punkt Z liegt somit auf der Halbsehne FG von früher.
Die Verbindungsgerade des Mittelpunktes M des grossen
Halbkreises mit Z schneidet den grossen Halbkreis mm Punkt W ,
dem Berührungspunkt "meines" Kreises mit dem grossen Halbkreis.
Wir bezeichnen den Radius dieses letztern Kreises mit y.
Es gilt y = ZW = ZF .
Wir können y mit Hilfe des Satzes von Pythagoras, angewandt auf
das Dreieck FZM , berechnen.
Kathete MF = R - 2 a, wobei R = a + b gilt; ferner ist:
FZ = y
MZ = R - y
Gleichung für y :
y ^ 2 = ( R - y ) ^ 2 - ( R - 2 a ) ^ 2 , daraus:
y = 2 * a * b / ( a + b ) .
Der Radius des von Dir erwähnten dritten Kreises ist y/2 ,
ein Wert, den wir erwartet hatten.
Mit freundlichen Grüssen
H.R,.Moser,megamath.
. |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Donnerstag, den 28. Juni, 2001 - 14:33: | 
|
Besten Dank !
(Ich dachte mir schon, dass mit der Revanche-Aufgabe etwas nicht stimmt...)
Doch: der Marathon geht weiter !
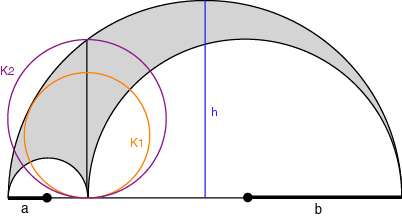
Sei K1 der Kreis welcher den Fusspunkt der Halbsehne durchläuft und den grössten Halbkreis berührt. K2 ist der Kreis, dessen Durchmesser der Halbsehne entspricht und h ist die Höhe der ganzen Figur.
Man zeige:
- Der Durchmesser von K1 ist das harmonische Mittel von a und b
- Der Durchmesser von K2 ist das geometrische Mittel von a und b
- Die Höhe h ist das arithmetische Mittel von a und b |
    
Pascal Rolli (Prolli)

| | Veröffentlicht am Donnerstag, den 28. Juni, 2001 - 14:41: | 
|
Ergänzung: a und b seien dieses Mal die Durchmesser |
    
H.R.Moser,megamath.

| | Veröffentlicht am Freitag, den 29. Juni, 2001 - 09:59: | 
|
Hi Pascal,
Deine neuesten Fragen sind nicht schwierig zu beantworten.
Ich gebe Dir Lösungshinweise, die Dir helfen sollen , die drei
Behauptungen locker zu bestätigen
Wir legen zuerst Bezeichnungen fest.
AB ist nach wie vor der Durchmesser des grössten Halbkreises k*
mit Mittelpunkt M und Radius R
Der Radius des kleinen Halbkreises links ist immer noch a,
der Durchmesser sei p; der Radius des kleinen Halbkreises ist
wiederum b, der Durchmesser sei q.
FG ist nach wie vor die auf AB in F senkrecht stehende Halbsehne .
Z sei der Mittelpunkt des Kreises k1,der AB in F und den Halbkreis k*
im Punkt J berührt. Der Radius dieses Kreises sei f ,der Durchmesser g .
Die drei Mittel von p und q lauten:
Arithmetisches Mittel m1 =: ½ * (p + q)
Geometrisches Mittel m2 = wurzel( p* q )
Harmonisches Mittel m3 = 2*p*q / (p+q)
..............N.B .es gilt 1 / m3 = ½ * ( 1 / p + 1 / q )
Lösungshinweise
1.
a+b = R, p = 2 a . q = 2 b , daraus findet man sofort m1. = R = h.
2.
Im rechtwinkligen Dreieck AG B schreibe man den Höhensatz an.
Damit erhalten wir m2.
3.
Im rechtwinkligen Dreieck MFH schreibe man den Satz des Pythagoras
an
Daten: Kathete MF = R- p, Kathete ZF = f
Hypotenuse MZ = R - f. ( Berührung der Kreise in J )
Aus der wurzelfreien Gleichung wird f berechnet; Resultat:
f = (2 p R - p^2) / (2*R) = 2 a b / (a+b) = p q /(p+q),also
g = 2 * f = 2 p q / (p+q) = m3
°°°°°°°°°°°°°°°°°°°°°°°°°°°°°°
Mit freundlichen Grüssen
H.R.Moser,megamath. |
|