| Autor |
Beitrag |
    
Lukas Köster (Luke18)

| | Veröffentlicht am Mittwoch, den 07. März, 2001 - 16:32: | 
|
Ich muss unbendingt wissen wie die
1)Definitionsmenge
2)Lösungsmenge
3)Polstellen
4)Definitionslücken
5)Asymptotenfunktion "gegen welche
Funktionsgrenze läuft die Funktion für große und kleine x-Werte?"
6)y-Achsenabschnitt
von dieser Formel is:
f(x)=(2x^2+2x-4)/(x^2+x-6)
Ich weiss das ist viel aber ich raff davon gar nix
weiss auch vielleicht jemand wo ich das richtig erklärt bekomme?
THX for help |
    
Ysanne (Ysanne)

| | Veröffentlicht am Mittwoch, den 07. März, 2001 - 18:46: | 
|
Zum Beispiel bei einem Nachhilfelehrer. Oder dem Klassenbesten.
Definitionsmenge:
Definitionsmenge heißt "Die Menge aller Zahlen, die man einsetzen darf". Was darf man nicht einsetzen? Zahlen, bei denen...
...unter einer Wurzel was negatives steht
...irgendein Nenner null wird
oder sonst etwas nicht-erlaubtes eingesetzt wird.
Hier zum Beispiel gibt es nur den Nenner, der nicht 0 werden darf. Wann wird er das?
(x² + x - 6) = 0
Vieta:
(x - 2)(x + 3) = 0
Das wird 0 wenn (x-2) oder (x+3) 0 wird, also bei x = 2 und x = -3. Diese beiden Zahlen darf man nicht einsetzen. Alle anderen schon. Also:
D = R\ {-3;2}. Die Definitionslücken sind somit -3 und 2.
Lösungsmenge- von was denn? Ich denke mal du willst die Nullstellen. Die rechnet man so aus:
Ein Bruch wird genau dann 0, wenn sein Zähler 0 ist. Sonst nicht, wer soll ihn denn sonst so klein machen. Klar, oder?
Also suchen wir die Nullstellen des Zählers.
2x² + 2x -4 = 0 |:2
x² + x - 2 = 0
Vieta:
(x - 1)(x + 2) = 0
Also Nullstellen wenn (x-1) oder (x+2) 0 ist, d.h. bei 1 und -2.
Polstellen: An einem Pol haut die Funktion nach Unendlich ab, d.h. ist dort nicht definiert. Also kann sowas schon mal nur an einer Def.-Lücke passieren.
Aber schreiben wir f(x) erst mal faktorisiert hin...
f(x) = ((x - 1)(x + 2))/((x - 2)(x + 3))
Wir sehen daß wir nichts wegkürzen können.
Wie kommt es eigentlich zu einer Polstelle? Eigentlich so, daß der Zähler gegen einen festen Wert strebt (z.b 2) und der Nenner aber gegen 0. Wenn man eine praktisch feste Zahl durch etwas ganz ganz Kleines teilt, paßt das Kleine ja furchtbar oft rein, d.h. es kommt was sehr Großes (betragsmäßig) raus. Bei einer Polstelle strebt eine Klammer im Nenner gegen 0 und der Zähler gegen was festes. Deshalb wird, je näher man an den Punkt kommt, der Funktionswert (betragsmäßig) immer größer und größer.
Also haben wir Polstellen bei -3 und 2.
Untersuchen wir das Verhalten von f(x) an ihnen:
Bei x=-3 ist der Zähler 2*9-4-4=10, also positiv (in der näheren Umgebung auch).
Die nicht-0-strebende Nenner-Klammer ist -3-2=-5 also negativ. Und wenn wir bei was kleinerem als -3 sind, ist auch x+3 negativ. Auf der linken Seite vom Pol ist f(x) also +/(-*-) = +, geht also nach +unendlich. Da nur (x+3) beim darübergehen das Vorzeichen gewechselt hat, ist f(x) rechts vom Pol negativ geworden. Dort geht es also gegen -unendlich.
Genau dasselbe Spielchen machen wir bei 2:
Links davon ist der Zähler 2*4+4-4=8, also +, x+3 ist auch +, und x-2 ist noch -, d.h. der Graph geht nach -unendlich. Da auf der rechten Seite des Pols schon wieder alles positiv ist, geht es da nach +unendlich.
Kleiner Zusatz: Wenn im Zähler und Nenner die gleiche Klammer vorkäme, wäre das natürlich keine Polstelle, sondern einfach nur ein Loch in der Funktion. Schließlich kann man das kürzen.
Asymptote:
Hierbei geht es einfach darum, mal wirklich die Polynomdivision durchzuführen, und die Sachen mit x im Nenner verschwinden, wenn man dann x -> unendlich macht.
Also Polynomdividieren, es kommt 2 + 8/(x²+x-6) raus.
Für x->+unendlich geht (x²+x-6) gegen +unendlich (Parabel nach oben geöffnet), 8/(x²+x-6) also gegen 0 (von oben), und somit f(x) gegen 2 (von oben).
Für x->-unendlich geht (x²+x-6) auch gegen +unendlich, also 8/(x²+x-6) gegen 0 von oben, also f(x) gegen 2 von oben.
y-Achsenabschnitt: Ja wo ist denn die y-Achse? Dort, wo x=0 herrscht. Also einfach Einsetzen:
y = f(0) = -4
Graph ist dann:
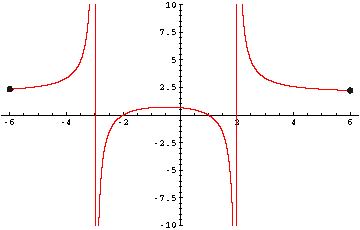 |
    
Lukas Köster (Luke18)

| | Veröffentlicht am Mittwoch, den 07. März, 2001 - 20:04: | 
|
Jo is korreckt...hätte nich gedacht so schnell antwort zu bekommen. Hat mir jetzt geholfen den wirrwar vom Lehrer besser zu raffen ;)
thx |
    
Ysanne (Ysanne)

| | Veröffentlicht am Donnerstag, den 08. März, 2001 - 13:26: | 
|
ahem, also... wie man deutlich sieht hab ich mich beim y-abschnitt gut verrechnet... tschuldigung...
ist natürlich -4/-6 = 2/3 |
|