| Autor |
Beitrag |
    
Katharina Krüger (Amati)

| | Veröffentlicht am Mittwoch, den 06. Dezember, 2000 - 09:09: | 
|
hallo leute
wie beweise ich folgenden satz:
" im gleichschenkligen dreieck ABC sei D ein beliebiger punkt der basis AB. beweise: Die umkreise der dreiecke ADC und DBC haben einen gleichlangen radius."
könntet ihr mir dabei helfen?
tschüss, katharina |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 06. Dezember, 2000 - 23:28: | 
|
 |
    
B.Bernd

| | Veröffentlicht am Mittwoch, den 06. Dezember, 2000 - 23:34: | 
|
Hi Katharina, ich hoffe, dass du schon in der 10 bist, denn auf den Sinussatz kann ich hierbei nicht verzichten.
Sinussatz: außer den Verhältnissen a/sin(a) = b/sin(b) = c/sin(g) gilt auch noch, dass dies = 2r ist, wobei r der Umkreisradius ist.
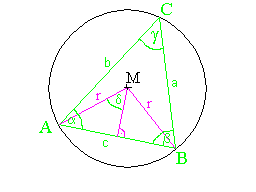
Das wird bei Betrachtung der Skizze klar:
sin(d) = (c/2)/r = c/(2r), nach dem Satz vom Mittelpunktswinkel (7. oder 8. Kl.: In einem Kreis ist der Mittelpunktswinkel doppelt so groß wie jeder Umfangswinkel über demselben Bogen), hier also Mittelpunktswinkel 2d doppelt so groß wie Umfangswinkel g, also 2d = 2g, also d = g.
Damit gilt sin(g) = c/(2r).
Ab jetzt beziehen sich alle Bezeichnungen auf dein/e Dreieck/e:
Ebenso gelten sin(a) = a/(2r) und sin(b) = b/(2r), für die Dreiecke ADC und DBC:
a=|DC|=b, a ist der Winkel zwischen den Seiten AD und CA, b ist der Winkel zwischen den Seiten DB und BC.
Damit folgt sin(a) = a/(2rADC) = |DC|/2rADC und sin(b) = b/(2rDBC) = |DC|/2rDBC , und da nach Voraussetzung, dass ABC ein gleichschenkliges Dreieck mit Basiswinkeln a und b ist, gilt, dass a=b, gilt auch |DC|/2rADC = |DC|/2rDBC , und somit rADC = rDBC , was zu zeigen war. |
|