| Autor |
Beitrag |
    
Püppy

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 23. April, 2002 - 13:04: | 
|
Kann mir jemand helfen diese umfangreiche Aufgabe zu lösen?
a)Berechne die Länge der Raumdiagonale eines Würfels mit der Kantenlänge 8cm.
b)Stelle eine Formel auf,mit der du bei gegebener
Kantenlänge die Diagonale berechnen kannst.
c)Berechne mit der in b9 gefundenen Formel,welche Kantenlänge ein Würfel hat,dessen Raumdiagonale
10 cm lang ist.
Vielen Dank im voraus!!!!!!!!! |
    
Alfred

Unregistrierter Gast
| | Veröffentlicht am Dienstag, den 23. April, 2002 - 17:05: | 
|
Hallo Püppy,
Tipp: mach dir mal eine Skizze, dann wirds ganz einfach!
Rechne dann allgemein, z.B. Kantenlänge = a.
Gruß Alfred
|
    
Lars (thawk)

Fortgeschrittenes Mitglied
Benutzername: thawk
Nummer des Beitrags: 142
Registriert: 12-2000
| | Veröffentlicht am Dienstag, den 23. April, 2002 - 20:30: | 
|
Okay Püppy.
Ein bisschen ausführlicher kann wohl nicht schaden.
Ich hab dir noch mal eine Skizze gemacht - ich weiß, sie sieht nicht so toll aus aber der Sachverhalt dürfte klar werden.
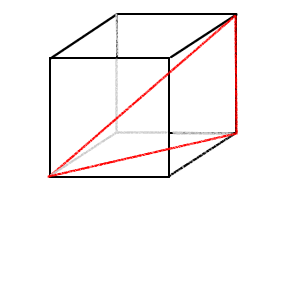
Die rote Linie, die sich durch den Würfel von einer Ecke zur anderen zieht ist die gesuchte Raumdiagonale. Diese ist gleichzeigt Hyopthenuse des roten Dreiecks (rechter Winkel beim hinteren rechten Punkt).
Also ist der Satz des Pythagoras anwendbar. Dafür brauchst du allerdings erst die Länge der "Grundflächen-Halbierenden" (also der unteren roten Strecke). Diese errechnet sich ebenfalls mit dem Satz des Pythagoras.
Es ergibt sich:
h2 = 82 + 82
=> h = SQRT(128) [SQRT bedeutet "2. Wurzel aus"]
<=> h = 11,32 [gerundet]
h ist die "Grundflächen-halbierende".
Jetzt setzt du ein in den Satz des Pythagoras zur Berechnung der Raumdiagonalen d:
d2 = h2 + 82
<=> d2 = 128 + 64
<=> d = SQRT(194)
<=> d = 13,93
zur Teilaufgabe b)
==================
Hierfür musst du dir eigentlich nur überlegen, was du oben gerechnet hast und die beiden Formeln zusammenpacken.
Zweiter Schritt war: d = SQRT(h2 + a2)
wobei d die Raumdiagonale, h die "Grundflächendiagonale" und a die Seitenlänge darstellt.
h2 ist ja nicht gegeben sondern wurde im ersten Schritt ausgerechnet: h2 = 2 * a2
Jetzt setzt du für h2 in der Formel des zweiten Schrittes das Ergebnis des ersten Schritts ein und erhälst:
d = SQRT(2 * a2 + a2)
Das kannst du jetzt natürlich noch zusammenfassen und erhälst:
d = SQRT(3 a2)
oder mit teilweisem radizieren:
d = SQRT(3) * a
Teilaufgabe c dürfte aber jetzt wirklich kein Problem mehr sein, oder?
Machs gut,
Lars |
|