| Autor |
Beitrag |
    
uli

| | Veröffentlicht am Sonntag, den 07. Mai, 2000 - 08:40: | 
|
Hallo!
Ich bin die uli und hätte gern ein paar Aufgaben zum Satz des Pythagoras.
Vielen Dank! |
    
reinhard (Gismo)

| | Veröffentlicht am Sonntag, den 07. Mai, 2000 - 12:04: | 
|
Hallo Uli!
Am besten klickst du auf der linken Seite auf "Archivsuche - Nach Stichwort". Dort gib dann "Pythagoras" als Suchbegriff ein, und schon bald werden dir alle im Bord verfügbaren Nachrichten, die den Pythagoras enthalten, aufgelistet. Ich denke das sind für den Anfang mal genug Beispiele.
Reinhard |
    
Pi*Daumen

| | Veröffentlicht am Sonntag, den 07. Mai, 2000 - 15:41: | 
|
Oder Du klickst direkt hier:
Pythagoras
Pi*Daumen |
    
Kadmax

| | Veröffentlicht am Donnerstag, den 18. Mai, 2000 - 15:06: | 
|
Hi,
Wer kann den Satz des Pythagoras beweisen:
kann mir einer den Satz des Pythagoras, in einzelnen begründeten Schritten bewisen.
Damit ich es auch endlich kapire.
Es ist eilig
Danke. |
    
Bodo

| | Veröffentlicht am Freitag, den 19. Mai, 2000 - 21:59: | 
|
Hier sind Beweise:
http://sunsite.univie.ac.at/MathAnim/pythanim.gif
http://didaktik.physik.uni-wuerzburg.de/~pkrahmer/java/pythago/pythago.html
http://www.cinderella.de/Demo/Book/PythagorasProof.html
29 Beweise des Satzes des Pythagoras - english
Hintergrundinfos über den Satz des Pythagoras
Bodo |
    
Chrisi

| | Veröffentlicht am Dienstag, den 27. Juni, 2000 - 12:20: | 
|
Wer kann diese aufgabe:
Der Umfang eines Rechtecks beträgt 82cm, die Diagonale ist 9cm länger als eine der beiden Seiten. Wie lang sind die Seiten?
danke, chrisi |
    
MDorff

| | Veröffentlicht am Dienstag, den 27. Juni, 2000 - 19:45: | 
|
Hi, Chrisi,
geg: u=82cm und d=a+9
2 Formeln stehen zur Verfügung:
u=2(a+b)
84=2(a+b)
a+b=42
b=42-a (A)
a2+b2=d2
a2+b2=(a+9)2
a2+b2=a2+18a+81
Für b setzen wir nun Gleichung (A) ein:
a2+(42-a)2=a\+72}+18a+81
a2-102a+1683=0
a1/2=51+-Wurzel aus (2601-1683)
a1=20,7.
Wenn a=20,7cm (rechne nach, warum a2 ausscheidet),
so b=42-20,7=21,3cm.
Wir machen eine Probe:
d2=20,72+21,72
d =29,7cm und damit 9 cm länger als a(20,7cm).
Verstanden ? |
    
tina

| | Veröffentlicht am Donnerstag, den 03. August, 2000 - 22:18: | 
|
Hallo Leute,
ich bin Referendarin an einer Hauptschule und suche dringend einen guten Unterrichtsentwurf zum Beweis des Satzes von Pythagoras. Wer kann mir helfen. Es eilt!! Vielen Dank!!
Tina |
    
Georg (Georg)

| | Veröffentlicht am Donnerstag, den 03. August, 2000 - 23:39: | 
|
Ich bin kein Lehrer und weiß daher nicht, ob Sekundarstufe 1 passt.
Aber die Idee, metager "Mathematik Pythagoras" zu fragen, führte u. a. zu folgender Adresse :
http://www.bildung.hessen.de/fbereich/mathe/ski/9und10/pythago/ |
    
Niels

| | Veröffentlicht am Freitag, den 04. August, 2000 - 07:36: | 
|
Hallo Tina,
also mein Mathelehrer hatte damals per Scherung die Kathetensätze bewiesen und aus ihnen dann den Pythagoras abgeleitet. Den Höhensatz haben wir dann damals Algebraisch bewiesen.
Gruß N. |
    
Danny (Danny)

| | Veröffentlicht am Freitag, den 04. August, 2000 - 09:44: | 
|
Hi Tina!
Ich habe dazu folgende Zeichnung gefunden:
Ciao
Danny |
    
OliverKnieps (Oliverk)

| | Veröffentlicht am Freitag, den 04. August, 2000 - 22:34: | 
|
Hallo Tina,
es gibt weit über hundert verschiedene Beweise zum Satz des Phytagoras, den wohl gängisten möchte ich hier kurz anführen.
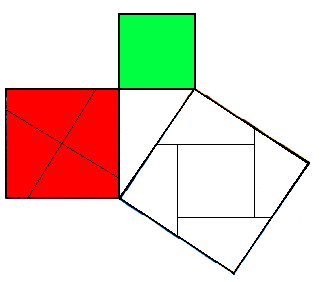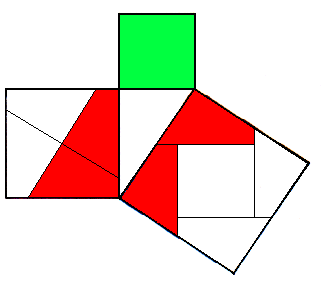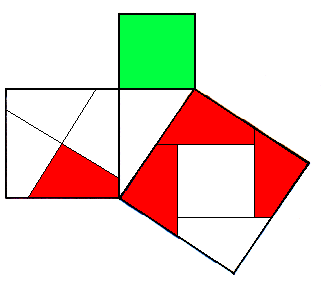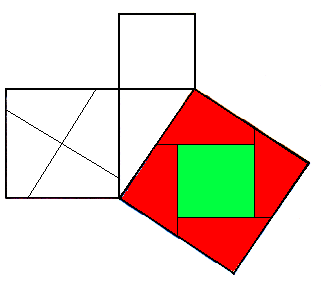
Das folgende Bild habe ich nur schnell erstellt. Das quer in das große Quadrat eingeschriebene Quadrat hat natürlich zueinander parallele Seiten!

Für den Flächeninhalt des großen Quadrates gilt:
A = (a+b)(a+b)=(a+b)2
und diese Fläche können wir auch anders ausdrücken, wir addieren dazu die Flächeninhalte des schiefen Quadrats und das der 4 kleinen, rechtwinkligen Dreiecke, also
A = c2 + 4*(1/2*a*b)
A = c2 + 2 ab
also gilt dann
(a+b)2 = c2 + 2ab
a2 + 2ab + b2 = c2 + 2ab
und schließlich finden wir
a2 + b2 = c2
was zu beweisen war.
Dieser Beweis ist übrigens der erste von Phytagoras. Er selbst fand noch viele weitere, übrigens auch ein ebenso prominenter Zeitgenosse um 19. Jahrhundert. Sein Name: Abraham Lincoln.
Viele Grüße an die Schüler
 Oliver Oliver |
    
tina

| | Veröffentlicht am Freitag, den 11. August, 2000 - 10:50: | 
|
Leute, ihr seid spitze!!
Vielen Dank für die vielen Tipps und Tricks, die ihr mir in den letzten Tagen hier habt zukommen lassen. Daraus lässt sich was machen!!
Mal gucken, was meine 9.Klasse nach den Sommerferien dazu sagt.
Liebe Grüße von Tina |
    
Das Genie

| | Veröffentlicht am Mittwoch, den 30. August, 2000 - 18:59: | 
|
Die Lösung von MDorff zur Chrisi´s(bist du schwul oder warum nennst du dich so)Aufgabe ist leider falsch. Die Korrekte Lösung lautet: a=20cm und b=21cm. Da musst du noch einbißchen Üben bevor du versuchst solche Aufgaben zu Lösen. |
    
Kriemhild Wietrzykowski (Sammy)

| | Veröffentlicht am Montag, den 13. November, 2000 - 21:27: | 
|
Hallo Leute!Wer kann mir eine Antwort bis morgen früh geben wäre super nett von euch!Also Berechne die Quadrate über den kürzeren Seiten im rechtwinkligen Dreieck. Wie groß ist das Quadrat über der Seite c? A) a= 7cm b= 9cm B) a= 8cm b= 15cm C)a= 11cm b= 9cm Danke Sammy |
    
Gerd

| | Veröffentlicht am Dienstag, den 14. November, 2000 - 00:57: | 
|
A) a2=49cm2, b2=81cm2 => (Pyhagoras) c2=a2+b2=49cm2+81cm2=130cm2
Okay? Die anderen beiden gehen exakt nach dem gleichen Strickmuster, einfach die Zahlen einsetzen.
Gerd |
    
Gerd

| | Veröffentlicht am Dienstag, den 14. November, 2000 - 00:58: | 
|
Wenn Du bei neuen Fragen einen neuen Beitrag aufmachst, dann ist die Chance am größten, daß die Aufgabe jemand findet. War eben bei mir ein Zufallstreffer ;-)
Gerd |
    
Wibke

| | Veröffentlicht am Sonntag, den 19. November, 2000 - 18:27: | 
|
Hallo Leute!
Wer kann mir bis spätestens Donnerstag den Satz des Pythagoras an Hand eines Beispiels mit jeder kleinsten Handlung erklären? Und dazu schreiben, warum das nun so ist! Danke!
Und wer erkärt mir diese Aufgabe bis MORGEN?
Wenn von einer regelmäßigen Pyramide mit quadratischer Grundfläche zwei der Längen a,h,k,s
bekannt sind,kann man die anderen beiden berechnen. Wie macht man das?
a) Stell für die Aufgaben einen Lösungsplan auf
b)Berechne die fehlenden Längen:
1.)h=5m s=8m
2.)h=4,50m k=7,50m
Nochmals DANKE!!!!!
Wibke |
    
Leo (Leo)

| | Veröffentlicht am Montag, den 20. November, 2000 - 20:53: | 
|
Beispiele findest Du hier: ...Pythagoras
Du findest in einer solchen Pyramide sehr viele rechteckige Dreiecke, deren Hypothenuse (Seite gegenüber dem rechten Winkel) oder auch die Katheten, je nachdem, was gegeben ist, ausrechnen kannst (Pythagoras) Suche solche Dreiecke und schau nach ob Du mit den gegeben Größen auf die anderen schließen kannst.
Den Satz von Pythagoras und die Formeln für eine Pyramide mit quadratischer Grundfläche findest Du im Online-Mathebuch |
    
Kathrin

| | Veröffentlicht am Montag, den 04. Dezember, 2000 - 19:04: | 
|
Kann mir jemand von euch sagen, wie ich eine Formel zur Errechnung alle pytagorianischen Zahlen finde. Das heißt zum Beispiel:3²+4²=5²
Kathrin Bitte möglichst schnell |
    
anonym

| | Veröffentlicht am Montag, den 04. Dezember, 2000 - 20:49: | 
|
Nur wenn Du bei einer neuen Frage auch einen neuen Beitrag öffnest! |
    
Martin

| | Veröffentlicht am Montag, den 04. Dezember, 2000 - 21:02: | 
|
Du nimmst einfach 2 beliebige Zahlen m und n. (m>n)
Dann rechnest du daraus wie folgt a, b und c aus
a=m²-n²
b=2mn
c=m²+n²
Es gilt nun a²+b²=c²
Mit dieser Methode bekommst du alle pytagoräischen Zahlentripel.
Willst du, dass a, b und c teilerfremd sind, musst du m und n so wählen, dass m teilerfremd zu n ist und m und n nicht gleichzeitig ungerade sind. |
    
Dominik

| | Veröffentlicht am Donnerstag, den 14. Dezember, 2000 - 13:03: | 
|
Wenn in einem Dreieck die Bezeichung h²=p*q gilt, dann ist das Dreiceck rechtwinklig.
Zeiche ein beliebiges Dreieck ABC, errichte im Punkt C die Höhe hc=h mit dem Fußpunkt D und bezeichne AD=q und DB=p!
Nimm nun an, dass in diesem Dreieck h²=p*w gilt! Beweise dass das Dreieck in diesem Fall rechtwinklig sein muss!
---> ??? Kann mir das jemand erklären? |
    
Karl

| | Veröffentlicht am Donnerstag, den 14. Dezember, 2000 - 21:41: | 
|
Bei neuer Frage: neuen Beitrag öffnen. |
    
Monalisa

| | Veröffentlicht am Donnerstag, den 14. Dezember, 2000 - 21:44: | 
|
Was sind pythagoräische Zahlen? |
    
Kai

| | Veröffentlicht am Freitag, den 15. Dezember, 2000 - 18:23: | 
|
a,b,c sind pythagoräische Zahlen, wenn a2+b2=c2 gilt.
Bsp.: 6,8,10 oder 5,12,13.
Kai |
    
Cora

| | Veröffentlicht am Dienstag, den 19. Dezember, 2000 - 18:39: | 
|
Wir schreiben morgen eine Mathearbeit über den Satz des Phytagoras.Normalerweise bin ich gar nicht so schlecht in Mathe, aber wenn es um Geometrie geht, setzt bei mir alles aus.Kann mir jemand, der auch gerade online ist, diesen Mist mit Körper-und Flächendiagonalen erklären???Bitte!!!
Cora |
    
anonym

| | Veröffentlicht am Dienstag, den 19. Dezember, 2000 - 18:43: | 
|
Das ist Pech, wenn man den Satz des Phytagoras nicht richtig erklären kann.Leider geht es meiner Lehrerin genauso. Bei uns hat das keiner verstanden, außer unserem Klugscheißer.Viel Glück! |
    
/repost

| | Veröffentlicht am Donnerstag, den 11. Januar, 2001 - 14:07: | 
|
cih hab mal eine frage zu einer aufgabe, die indirekt mit dem satz des p zu tun hat, also man geht von der figur eines rechtwinkligen dreiecks mit den dazugehörigen quadraten aus, so wie es da oben auf der zeichnung von Danny der fall ist.
dann verbindet man die äußeren Eckpunkte der quadrate, sodass ein Sechseck entsteht. Nun brauche ich die Formel für den Flächeninhalt des Sechsecks.
thx
cya |
    
Matthias

| | Veröffentlicht am Freitag, den 12. Januar, 2001 - 16:30: | 
|
Wenn Du Dir die Figur aufzeichnest erhältst du 3 Quadrate , 2 rechtwinklige Dreiecke (eines davon ist das ursprüngliche Dreieck ABC) und 2 stumpfwinklige Dreiecke.
Das Kernproblem ist die Berechnung der Fläche der stumpfwinligen Dreiecke: Der stumpfe Winkel des linken stumpfwinkligen Dreiecks hat die Größe 180-alpha (denn alpha+90+90+180-alpha=360); analog beträgt der stumpfe Winkel des rechten stumpfwinkligen Dreiecks 180-beta.Dreht man das linke stw. Dreieck um 90 Grad "nach oben"(DrehpunktA) und ebenso das rechte stw. Dreieck (Drehpunkt B), so liegen die Dreiecke nun mit der Hypotenuse c des ursprünglichen Dreiecks ABC auf einer Geraden, wobei die je eine Ecke der stw. Dreiecke nun auf der Ecke C liegt.Jetzt erkennt man, das jedes der stw. Dreiecke den gleichen Flächeninhalt wie Dreieck ABC hat( denn Grundlinie(c) und Höhe (hc) sind gleich lang wie bei Dreieck ABC).
Der Flächeninhalt von Dreieck ABC ist (a*b)/2.
Also ist die Fläche der Gesamtfigur a^2+b^2+c^2+4*(a*b)/2 oder auch (da c^2=a^2+b^2)
2*a^2+2*b^2+2*a*b.
Alles klar??
mfg Matthias |
    
Oliver Köster (Hermann)

| | Veröffentlicht am Samstag, den 20. Januar, 2001 - 19:04: | 
|
Hi,
ich muss unbedingt wissen, wie man mit Hilfe des Kathetensatzes ( a² = c * p )vom Phytagoras eine Strecke mit der Länge Wurzel 24 zeichnet. Wenn jemand weiß, wie man das macht, soll er mir schreiben. Danke |
    
Bärbel Kranz (Fluffy)

| | Veröffentlicht am Samstag, den 20. Januar, 2001 - 23:00: | 
|
Hi Oliver,
ich kenn die Konstruktion von Wurzelwerten aus meiner Sculzeit (lang ists er!) nur mit der "Wurzelschnecke."
Und die geht so: Fang mit einem rechtwinkligen Dreieck an, dessen Katheten 1 cm lang sind. Die Hypotenuse ist dann Wurzel 2
Leg an diese Hypotenuse im rechten Winkel eine neue Kathete mit 1 cm Länge an. Das Ergebnis ist Wurzel 3 und so weiter.
Also an die neu erzeugten Hypotenusen immer wieder rechtwinklig eine Katete mit 1 cm anlegen, bis Du bei Wurzel 24 angekommen bist.
Vielleicht meint Dein Lehrer ja das.
Gruss Fluffy |
    
Zorro

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 11:14: | 
|
Hi Oliver, der Kathetensatz lautet ja a² = c*p.
Also mußt Du eine Konstruktion finden, bei der c und p so gewählt werden, daß a² = 24
Beispiel:
Man wähle c = 6 und p=4. Man erhält nach Kathetensatz a = Ö24
Nun zur Konstruktion:
1. Zeichne c = 6 cm
2. Errichte Thaleskreis über c
3. Trage p= 4 cm ab
4. Zeichne Sekrechte zu c durch P und ermittle den Schnittpunkt C
5. Die gesuchte Strecke ist der Abstand BC.
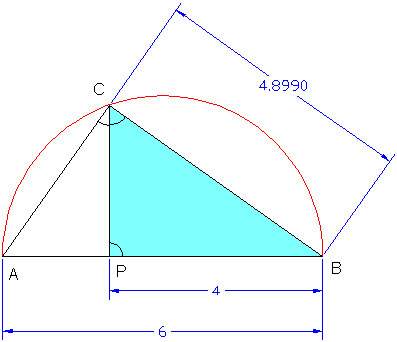
Gruß, Zorro |
    
Bärbel Kranz (Fluffy)

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 13:24: | 
|
Übrigens Oliver, dasselbe klappt auch mit c=8 cm und p=3 oder c=12 und p=2, denn auch das ergibt 24!!
Habe in meinem Gedächtnis gestöbert und kam, wenn auch zu spät, auf den gleichen Lösungsweg wie Zorro. Das ist eben der Vorteil der Jüngeren. Aber dieses Medium soll ja keine Wettkampfarena sein, sondern eine "Wissensbörse".
Gruss Fluffy |
    
Oliver Köster (Hermann)

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 14:02: | 
|
Danke an Fluffy und Zorro. Ihr habt mir sehr geholfen.
Gruß
Oliver |
    
weintrauben

| | Veröffentlicht am Dienstag, den 27. Februar, 2001 - 09:33: | 
|
finden wir ganz toll, und wir sind nicht voll.
nein, das sind wir wirklich nicht, sehen hier ganz viel licht... |
    
Melanie

| | Veröffentlicht am Donnerstag, den 29. März, 2001 - 12:58: | 
|
Hi ihr! Kann mir jemand erklären wie des beim Drachen und der Raute mit dem Satz gerechnet wird, bitte?????????? Wäre euch sehr dankbar!!!
Gruß Melanie |
    
katsche

| | Veröffentlicht am Donnerstag, den 29. März, 2001 - 13:47: | 
|
Hi Melanie!
Die Diagonalen schneiden sich im Drachen und in der Raute im rechten Winkel. Somit kannst du den Satz des Pytagoras anwenden. |
    
Melanie

| | Veröffentlicht am Freitag, den 30. März, 2001 - 19:01: | 
|
Hi Katsche!
Danke für die Erklärung, aber ich muss sagen
so viel habe ich schon selbst gewusst, das war nicht böse gemeint nimm es nicht falsch auf!!!!!
Nein ich meine damit ich verstehe, das ganze gerechne nicht, wenn da so eine blöde Aufgabe steht, dann verstehe ich sie nicht.
Wie z.b.Ist es möglich eine 5,20m lange und 2.10m breite, rechteckige Holzplatte durch eine Tür zu transportieren, die 2m hoch und 20 cm breit ist???
Kannst du mir diese Aufgabe lösen?????? |
    
thomas

| | Veröffentlicht am Donnerstag, den 17. Mai, 2001 - 18:38: | 
|
Hallo ich bin Thomas
Kann mir jemand sagen wie man den Satz des Pythagoras berechnet wenn man: die seite bund c hatt. und die seite a und c? Danke!! am besten wären die Formeln!!!!! |
    
Lerny

| | Veröffentlicht am Donnerstag, den 17. Mai, 2001 - 18:50: | 
|
Hi Thomas,
geht alles nur im rechtwinkligen Dreieck. Dem rechten Winkel gegenüber liegt die Hypothenuse. Die beiden anderen Seiten sind die Katheten.
Der Satz des Pythagoras lautet allgemein:
Im rechtwinkligen Dreieck ist das Quadrat über der Hypothenuse gleich der Summe der Quadrate über den Katheten.
Also:
Hypothenuse²(gegenüber rechtem Winkel)=Kathete1²+Kathete2²
Nun zu deinem Beispiel:
b und c gegeben; gesucht ist a
Liegt der rechte Winkel gegenüber von c, dann gilt:
a²+b²=c² |-b²
a²=c²-b² | Wurzel ziehen
a=Ö(c²-b²)
Liegt der rechte Winkel gegenüber von a, so gilt
a²=b²+c²
a=Ö(b²+c²)
Liegt der rechte Winkel gegenüber von b, so gilt:
b²=a²+c² |-c²
a²=b²-c² | Wurzel ziehen
a=Ö(b²-c²)
Hoffe ich konnte dir helfen.
mfg Lerny |
    
Undi

| | Veröffentlicht am Montag, den 24. September, 2001 - 16:31: | 
|
Ich hab da mal ne Frage: Kann mir bitte jemand den Satz des Pythagoras umstellen??? Alle Versionen. |
    
Andra

| | Veröffentlicht am Dienstag, den 25. September, 2001 - 09:16: | 
|
Hallo Undi,
bitte bei neuer Frage immer einen neuen Beitrag aufmachen.
Ciao, Andra |
    
lisa

| | Veröffentlicht am Mittwoch, den 03. Oktober, 2001 - 14:21: | 
|
Ich suche Infos zu den Pythagoreern. Ich muss ein Referat machen. Kann mir jemand Links oder Infos zukommen lassen? Lisa ;o) |
    
Ralph (Raz)

| | Veröffentlicht am Mittwoch, den 03. Oktober, 2001 - 14:30: | 
|
Hallo Lisa!
Vielleicht hilft dir
http://www-pool.mathematik.hu-berlin.de/~fsr/vl-gema1.html
weiter.
MfG
Ralph |
    
Sam

| | Veröffentlicht am Samstag, den 03. November, 2001 - 14:46: | 
|
Kennt jemand das Gedicht von Ernst Jandl, ottos mops?!
ottos mops
ottos mops trotzt
otto: fort mops fort
ottos mops hopst fort
.
.
.
ich begreife das Gedicht nicht ganz!muss jetzt aber für die schule ein solches schreiben!
und sonst wenn ihr andere tolle Gedichte kennt ist auch in Ordnung!
Danke, Sam |
    
Friedolin

| | Veröffentlicht am Samstag, den 03. November, 2001 - 17:15: | 
|
hallo Sam,
Warum öffnest Du keinen neuen beitrag? |
    
netti

| | Veröffentlicht am Dienstag, den 20. November, 2001 - 20:06: | 
|
hilfe,
wie geht das????????????
Konstruiere mithilfe des satzes des pythagoras ein quadrat mit dem flächeninhalt A=2cm²!
eigentlich einfach,aber für mich nicht! |
    
Alfred Kubik (Fredy)

| | Veröffentlicht am Dienstag, den 20. November, 2001 - 22:31: | 
|
Hallo Netti,
Flächeninhalt des Quadrates:
A = a*a
2=a²
a=Ö2
Diesen Wert kannst du natürlich nicht genau zeichnen, da Ö2=1,4142.... ist.
Mit Pythagoras kannst du aber die Diagonale des Quadrates, das eine Seitenlänge a=Ö2 hat berechnen:
a²+a²=d² ...d=Diagonale
(Ö2)²+(Ö2)²=d²
d²=4
d=Ö4
d=2
In einem Quadrat stehen die Diagonalen senkrecht aufeinander und halbieren sich.
Daher kannst du nun eine Diagonale mit 2cm zeichnen, konstruiere die Senkrechte im Halbierungspunkt von d und schlage vom Schnittpunkt je 1cm auf der nun gefundene 2.Diagonale ab.
Du hast jetzt alle 4 Eckpunkte ABCD des Quadrates und kannst es nun fertig zeichnen!
Okay?
Grüße,
Fredy |
|