| Autor |
Beitrag |
    
Julia Söllner

| | Veröffentlicht am Sonntag, den 19. März, 2000 - 14:42: | 
|
Hallo ich bräuchte bitte eine Lösung für folgende
Aufgaben:
1. Zeichne ein Dreieck ABC mit gamma = 90°.
Hc ist der Höhenfußpunkt auf c. Die Halbierende
des Winkels HcCB schneidet c in D.
Beweise: Das Dreieck ADC ist gleichschenklig.
2. Im Dreieck ABC ist gamma doppelt so groß wie
beta. Die Winkelhalbierende w von gamma
schneidet c in D.
Beweise: Die Parallele zu a durch D halbiert
den Winkeln ADC.
Vielen Dank schon mal im voraus.
Tschüss Julia |
    
reinhard

| | Veröffentlicht am Sonntag, den 19. März, 2000 - 19:31: | 
|
Hallo Julia!
1.)
Ich nenne den Winkel in B einfach b.
Das Dreieck BCHc ist rechtwinkelig. Da der Winkel HBC b ist, ist der Winkel HcCB gleich 90-b. Die Strecke CD ist die Winkelhalbierende eben dieses Winkels, also ist der Winkel HcCD gleich (90-b)/2=45-b/2.
Auch das Dreieck HcCD ist rechtwinkelig und da der Winkel HcCD wie eben festgestellt 45-b/2 ist, beträgt der Winkel HcDC 90-(45-b/2)=45+b/2.
Wenn der Winkel HcCB, wie schon festgestellt, 90-b ist, und der Winkel ACB 90° ist, dann ist der Winkel ACHc 90-(90-b)=b.
Im Dreieck ACD wissen wir also folgendes:
der Winkel ADC ist 45+b/2 (wie schon festgestellt) und der Winkel ACD ist die Summe der Winkel ACHc und HcCD, also b + 45-b/2 = 45+b/2.
Die Winkel ACD und ADC sind also gleich, woraus folgt, daß dieses Dreieck gleichschenkelig ist.
2.
Die Parallele zu a durch D schneide die Seite b im Punkt E!
Der Winkel ABC sei wieder b. Da der Winkel BCA doppelt so groß ist, ist er 2b. die Strecke CD ist wieder die Halbierende eben dieses Winkels, weshalb git: Winkel BCD=b und Winkel DCA=b.
Im Dreieck CDB wissen wir: Winkel DCB=b und Winkel DBC=b, also Winkel CDB=180-2b.
Der Winkel ADC ist der Komplementärwinkel von BDC, also Winkel ADC=180-BDC=180-(180-2b)=2b.
Weiters sind, da die Strecke DE zu BC parallel ist, die Winkel ADE und die Winkel ABC parallelwinkel, also Winkel ADE=b.
Da der Winkel ADC aus der Summe von ADE und EDC besteht und ADC=2b und ADE=b folgt, daß EDC=b.
Somit ist die Strecke DE die Winkelhalbierende von ADC
Reinhard |
    
Susann

| | Veröffentlicht am Sonntag, den 02. April, 2000 - 12:41: | 
|
Hallo!
Brauche bitte dringend Lösung für folgende Aufgabe:
Dreieck ABCD hat eine besonders ansprechende Form;
sie läßt sich so beschreiben: Wenn man von diesem Rechteck ein Quadrat abschneidet, so hat das verbleibende Rechteck dieselbe Form wie das ursprüngliche, d.h. es ist
a:b=b:(a-b)(in Bruchstrich)
Rechtecke mit dieser Eigenschaft heissen "Goldene Rechtecke".
a)Bestätige, dass in goldenen Rechtecken für das Verhältnis v=a:b von kürzerer zu längerer Seite gilt: v=Wurzel5-1:2 (in Bruchstrich).
b) Zeige 1:v=1+v.
DANKE schon mal im vorraus!!!
Tschüss, sagt Susann. |
    
reinhard

| | Veröffentlicht am Sonntag, den 02. April, 2000 - 13:47: | 
|
Hallo Susann!
Du hast ja schon die vorgabe a:b=b:(a-b)
in den zwei Beweisen mußt du einfach ein bißchen einsetzen und umformen:
a)
v=a/b, also versuche ich in der angegebenen Formel solche Brüche herauszuarbeiten
a/b = b/(a-b)
ich invertiere beide Seiten
b/a=(a-b)/b
b/a=a/b-b/b=a/b-1
nun statt a/b v und statt b/a 1/v schreiben
1/v=v-1
1=v²-v
v²-v-1=0
Quadratische Lösungsformel:
v=1/2 ± wurzel(1/4+1) = 1/2±wurzel(5/4)=
negative v machen keinen Sinn (da a und b positiv sind)
v=1/2+wurzel(5)/2=(1+wurzel(5))/2
und das ist genau das, was zu zeigen war
b)
nimm die angegebene Formel und setzte a=1, b=v
1/v=v/(1-v)
v/1=(1-v)/v
v=1/v-v/v=1/v-1
v+1=1/v
1/v=1+v
und das wars auch schon wieder
Reinhard |
    
fredi

| | Veröffentlicht am Mittwoch, den 03. Mai, 2000 - 17:37: | 
|
hallo ich suche für mein mathematik-spezialgebiet die beweise für den TANGENTEN- UND SEKANTENSATZ und information über peripherie- und zentriwinkel!
danke
fredi |
    
Niels

| | Veröffentlicht am Donnerstag, den 04. Mai, 2000 - 18:47: | 
|
Hi Fredi,
schau mal unter Klassen 8-10/Geometrie/Sehnentangentenwinkel nach!
Dort hat Reinhard alles prima erkläret.
Gruß
Niels |
    
Anonym

| | Veröffentlicht am Samstag, den 06. Mai, 2000 - 17:03: | 
|
Hallo
Wieso ist in einem nichtgleichschenkligen Dreieck jede Seitenhalbierende länger als die zur gleichen Seite gehörende Winkelhalbierende? |
    
reinhard (Gismo)

| | Veröffentlicht am Sonntag, den 07. Mai, 2000 - 13:06: | 
|
Hallo!
Hier ein kleiner Beweis für diese Behauptung:
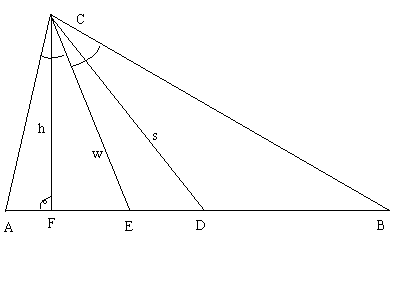
Im Dreieck ABC ist s die Seitenhalbierende und D der Punkt, wo die Seitenhalbierende die Seite c schneidet (also ist D der Mittelpunkt zwischen A und B)
die Winkelhalbierende ist w, und ihr Schnittpunkt mit der Seite c ist der Punkt E
Und dann habe ich noch die Höhe h eingezeichnet und deren Schnittpunkt mit der Seite c nenne ich F.
Ich nehe an, die Seite b ist die kürzere Seite (für den anderen Fall, daß a die kürzere seite ist, das Dreieck einfach spiegeln). Nun zeige ich, daß E immer näher bei A liegt, als D.
D liegt nämlich genau zwischen A und B. E hingegen hängt von den Seiten a und b ab. Es gibt nämlich einen Satz, der besagt, daß die Winkelhalbierende die gegenüberliegende Seite im selben Verhältnis wie die anliegenden Seiten schneidet. Also AC:AE = BC:BE
AE=BE*AC/BC
Da AC laut Annahme kleiner ist als BC, ist der Bruch AC/BC kleiner eins und somit die Länge AE kürzer als BE.
Der Punkt E liegt somit näher bei A als bei B, was heißt, daß E näher bei A liegt als der Punkt D, der ja genau in der Mitte liegt.
Als nächstes zeige ich, daß der Punkt F noch weiter bei A liegt als der Punkt E.
Weil die Seite b kleiner ist als die Seite a, ist der Winkel alpha im Punkt A (nach dem Sinus-Satz) größer als der Winkel beta im Punkt B.
Der Winkel gamma in C wird durch die Höhe h in zwei Winkeln unterteilt: in den Winkel ACF und FCB.
ACF berechnet sich mit 90°-alpha und FCB mit 90°-beta.
Ist alpha größer als beta, so ist 90°-alpha logischerweise kleiner als 90°-beta.
Die Winkelsymetrale hingegen teilt den Winkel gamma in zwei gleich große Winkeln, also der Winkel ACE ist gleich dem Winkel ECB.
Hier wieder dieselbe Überlegung wie oben schon:
Wenn der Winkel ACF ist kleiner als ACB und ACE ist genau in der Mitte von diesen beiden. somit ist ACF kleiner als ACE und damit der Punkt F näher beim Punkt A als der Punkt E.
Auf der Seite c liegen die Punkt F, E und D immer in genau dieser Reihenfolge, wobei die Dreiecke CFE und CFD rechtwinkelig sind.
CFE und CFD haben beide eine Kathete gemeinsam, nämlich die Höhe h.
Die zweite Kathete aber ist im Dreieck CFE kleiner als im Dreieck CFD, weil die Strecke FE kürzer ist als die Strecke FD (wie oben gezeigt).
Somit ist die Hypothenuse im Dreieck CFE, das ist die Winkelhalbierende, kürzer als die Hypothenuse im Dreieck CFD, also die Seitenhalbierende.
q.e.d.
Reinhard |
    
Anonym

| | Veröffentlicht am Montag, den 08. Mai, 2000 - 12:00: | 
|
Hallo!
Danke für den Beweis reinhard/Gismo. Aber was ist, wenn ich weder den Satz aus dem 2.Abschnitt noch den Sinus-Satz kenne, da ich erst in der 8.Klasse bin. Wie soll dann der Beweis aussehen? |
    
reinhard (Gismo)

| | Veröffentlicht am Montag, den 08. Mai, 2000 - 19:25: | 
|
Hallo!
Du machst es einem aber auch nicht leicht.
Auf den Sinussatz könnte ich ja noch verzichten, weil es beinahe offensichtlich ist, daß der Winkel bei der kürzeren Seite größer ist als der Winkel bei der längeren Seite, aber für den ersten Satz weiß ich jetzt momentan keine wirkliche Alternative, das heißt, ich wüßte schon welche, aber wie werden dir warscheinlich auch nichts nützen (zB mit der Dreiecks-Flächenformel A=a*b*sin(g)/2) - tut mir leid.
Reinhard |
    
Niels

| | Veröffentlicht am Dienstag, den 09. Mai, 2000 - 20:15: | 
|
Hallo Anonym,
kannst du etwas mit dem Begriff "Strahlensatz" anfangen?
CU
Niels |
    
Anonym

| | Veröffentlicht am Dienstag, den 09. Mai, 2000 - 20:36: | 
|
Hi Niels!
Nein,leider auch nicht. |
    
Fern

| | Veröffentlicht am Mittwoch, den 10. Mai, 2000 - 10:40: | 
|
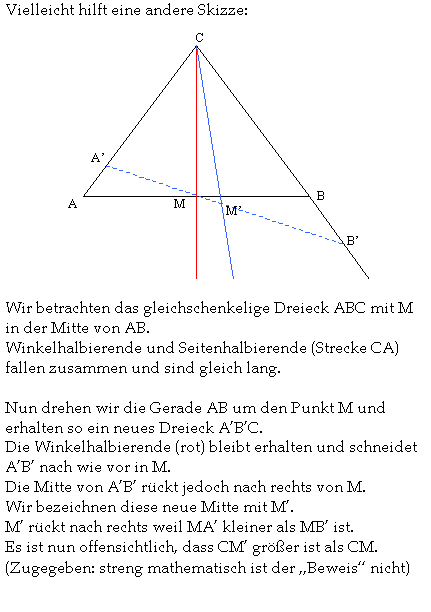 |
    
Zora

| | Veröffentlicht am Freitag, den 17. November, 2000 - 13:16: | 
|
Ich brauche dringend Hilfe
1.Aufgabe: Bewiese: Für alle natürlichen Zahlen m,n mit m > n ist das Dreieck ein rechtwinkliges Dreieck.
2. Aufgabe: Beweise: Wenn in dem Dreick gilt: a x a=y x c und b x b=x x c, dann ist das Dreieck rechtwinklig.
Schon mal danke im vorraus |
    
Bodo

| | Veröffentlicht am Freitag, den 17. November, 2000 - 15:42: | 
|
Hallo Zora, welches Dreieck meinst Du denn?
Skizze?
Bodo |
|