| Autor |
Beitrag |
    
Ute

| | Veröffentlicht am Samstag, den 13. Oktober, 2001 - 16:01: | 
|
Bitte helft mir mit der Aufgabe!!!
Einem gleichschenklig-rechtwinkligen Dreieck ABC mit gegebener Länge a der beiden Katheden AB, AC sind Rechtecke so einzuzeichnen, dass jeweils ein -eckpunkt eines solchen Rechteckes auf der Hypotenuse und zwei Rechteckseiten auf den katheden des Dreiecks ABC liegen.
a) Beweise, dass alle diese Rechtecke den gleichen Umfang u besitzen, nämlich u=2a.
b) Beweise, dass von allen diesen Rechtecken das unter ihnen enthaltene Quadrat den größten Flächeninhalt besitzt! |
    
R2D2

| | Veröffentlicht am Sonntag, den 14. Oktober, 2001 - 12:07: | 
|
kann dir leider auch net helfen, aber ich bin mir 100% sicher, dass ich die aufgabe letzte oder vorletzte woche schon mal gelesen hab. also schau doch mal im archiv nach! |
    
Lerny

| | Veröffentlicht am Sonntag, den 14. Oktober, 2001 - 20:33: | 
|
Hallo Ute
a)
zunächst eine Skizze
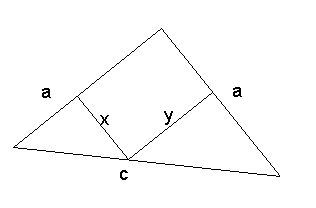
Mit dem Strahlensatz gilt
(a-y)/x=a/a also
(a-y)/x=1 |*x
a-y=x
Umfang(Rechteck)=2x+2y=2(a-y)+2y=2a-2y+2y=2a
b) A=x*y
=> A=(a-y)*y=ay-y²=-(y-a/2)²+a²/4
=> y=a/2
=> x=a-y=a-a/2=a/2
Damit gilt x=y also ein Quadrat.
mfg Lerny |
    
Tommy

| | Veröffentlicht am Montag, den 15. Oktober, 2001 - 11:05: | 
|
Hallo Lerny!
Du hast aber noch nicht bewiesen, dass dieses Quadrat den grössten Flächeninhalt hat! Bitte unbedingt anworten! Tommy |
    
Tommy

| | Veröffentlicht am Montag, den 15. Oktober, 2001 - 12:13: | 
|
Hallo Lerny!
Wie kommst du auf: ay-y²=-(y-a/2)²+a²/4 |
    
Lerny

| | Veröffentlicht am Montag, den 15. Oktober, 2001 - 12:25: | 
|
Hallo Tommy
alle Rechtecke haben den gleichen Umfang u=2a
Wenn Rechtecke den gleichen Umfang haben, dann ist das Quadrat dasjenige mit dem größten Flächeninhalt.
Könnte man mit Hilfe von Ableitungen beweisen (doch Klasse 8-10?)
ay-y²=-y²+ay=-(y²-ay) nun folgt eine quadratische Ergänzung
=-(y²-ay+(a/2)²-(a/2)²)
=-(y-(a/2))²+a²/4
mfg Lerny |
    
Tommy

| | Veröffentlicht am Montag, den 15. Oktober, 2001 - 17:29: | 
|
Hallo Lerny!
Das ist das Problem, es geht um Klasse 8.
Tschüss sagt Tommy |
|