| Autor |
Beitrag |
    
Methidfjd

| | Veröffentlicht am Samstag, den 24. Februar, 2001 - 10:46: | 
|
Wie berechnet man das Volumen und die Oberfläche? |
    
Carolin Römer (Siny)

| | Veröffentlicht am Sonntag, den 25. Februar, 2001 - 19:34: | 
|
Hallo. Heißt dieses Ding wirklich Kubooktaeder? Ich habe davon noch nichts gehört. |
    
Maren (Maha)

| | Veröffentlicht am Sonntag, den 25. Februar, 2001 - 21:41: | 
|
Hallo,
ein Kubooktaeder sieht so aus:
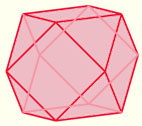
Sein Name lässt sich folgendermaßen ableiten:
Kubu kommt von Kubus= Würfel=> er hat 6 quadratische Seiten:

Otaeder: Eiin Oktaeder ist ein Gebilde mit 8 regelmäßigen dreieckigen Seiten (man kann es sich vorstellen wie 2 an der Grundfläche zusammengeklebte Pyramiden):
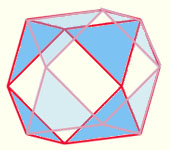
Um das Volumen und die Oberfläche zu berechnen sind folgende Überlegungen hilfreich:
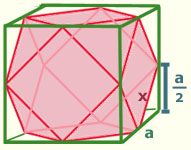
Er ist also quasi ein regelmäßig abgestumpfter Würfel, die Seiten a wurden genau halbiert.
x lässt sich demnach mit Pythagoras errechnen und wenn x berechnet wurde, kann man die Oberfläche ja schon mal ausrechnen.
Das, was man vom Würfel abschneidet sind 8 gleichmäßige Tetraeder. Mir fällt grad keine Volumen-Formel für den Oktaewder ein, aber man könnte einfach das Volumen der 8 Tetraeder von dem des Würfels abziehen.
Meinst du, dass du das hinbekommst?
Viel Spaß damit!
Grüße
Maren |
    
Frank (Norg)

| | Veröffentlicht am Montag, den 26. Februar, 2001 - 13:16: | 
|
Eine Frage an Maren:
Wie hast du denn die tollen Grafiken hinbekommen?
MfG Frank. |
    
Maren (Maha)

| | Veröffentlicht am Montag, den 26. Februar, 2001 - 16:56: | 
|
Hi Frank!
Mit photoshop,
Grüße
Maren |
    
c-eAGLE

| | Veröffentlicht am Montag, den 26. Februar, 2001 - 21:52: | 
|
Huhu!
Maren, was man da abschneidet, sind keine Tetraeder!!! Tetraeder haben 4 genau gleichgrosse Flaechen und 6 gleichlange Seiten, jedoch ist die jeweils innere Flaeche groesser als die restlichen 3 - so sind auch die Seitenlaengen der Seiten, die zur Spitze fuehren, nicht grundsaetzlich so lang wie die, die nicht zur Spitze fuehren!
Was man abschneidet, sind dreiseitige Pyramiden. Die Pyramiden hier haben die Eigenschaft, dass man sie aehnlich wie ein Dreieck berechnen kann, weil der Winkel der Pyramidenspitze ein 90°-Winkel ist: Wuerfel geteilt durch 2, in diesem Fall mit der Kantenlaenge a/2.
Ich bin einfach mal so frei und schreib ´ne hoffentlich richtige Formel hier hin, die ich mir sozusagen grad ausgedacht hab  ... ...
V = a ^ 3 - 8(((a / 2) ^ 3) / 2)
Falls das jemand nicht glaubt, hier meine Erklaerung:
a^3 ist der gesamte Wuerfel, von dem wir noch die 8 Pyramiden abziehen muessen.
Ohne jetzt zu beweisen, dass die Seitenlaengen der Pyramide, die zur Spitze fuehren, miteinander malgenommen einen Wuerfel ergeben, der genau doppelt so gross ist, als eine dieser Pyramiden selbst, hier die restliche Erklaerung:
a/2 ist jeweils eine der Seitenlaengen der Pyramiden, die zur Spitze fuehren.
Um einen Wuerfel daraus zu machen, muessen wir das ganze also ^3 nehmen. Dann durch 2 teilen und schon haben wir eine Pyramide.
Bis denn, c-eAGLE |
    
Maren (Maha)

| | Veröffentlicht am Montag, den 26. Februar, 2001 - 22:12: | 
|
Ja klar sorry...sind keine TETRAEDER...
;-)
Aber die Grafiken sind doch trotzdem schön, oder?! |8-)
Maren |
|