| Autor |
Beitrag |
    
Vredolf Ludrian (Vredolf)

Neues Mitglied
Benutzername: Vredolf
Nummer des Beitrags: 3
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 06. März, 2002 - 17:09: | 
|
Hallo,
Vielleicht hat jemand eine Idee dazu, obwohl es sich
hier um Denksport der härtesten Sorte handeln könnte. 
Eine Lösung existiert bisher nicht, daher kann ich nur
ein paar Anreize dazu geben:
Wir definieren die Funktion pp(k):
pp:=k->product((ithprime(2*n-1)/ithprime(2*n))^((-1)^(n+1)),n=1..k);
(maple-Notation)
also: pp(k) = 2/3 * 7/5 * 11/13 * 19/17 * ... * p(2k-1)/p(2k)
p(k) : k-te Primzahl
1) Man beweise oder widerlege: lim [k->oo] pp(k) existiert,
sprich pp(k) konvergiert
2) Man beweise oder widerlege: pp(k) < 1 für alle k
Viel Spaß damit, bin gespannt auf eure Ideen.
Nach ersten numerischen Berechnungen bis k=9999 sieht es
danach aus, dass der Grenzwert < 1 ist. Natürlich sagt
das noch nicht viel aus. :-)
mfg, Vred
P.S.: Hier noch ein plot von pp(k) im Intervall [1;3000]
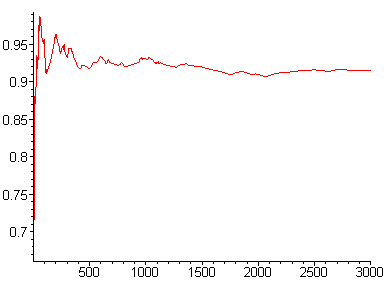 |
    
Zaph (Zaph)

Mitglied
Benutzername: Zaph
Nummer des Beitrags: 14
Registriert: 07-2000
| | Veröffentlicht am Mittwoch, den 06. März, 2002 - 20:13: | 
|
Setze doch mal
a(k) = p(2k-1)/p(2k), falls k gerade,
a(k) = p(2k)/p(2k-1), falls k ungerade.
Dann ist
pp(k) = a(1) * a(2) * ... * a(k).
Betrachte dann q(k) = log pp(k).
Es ist q(k) = S log a(k) = S b(k)
mit b(k) = log a(k).
b(k) bilden eine alternierende Folge, sind also abwechselnd größer/kleiner Null. Außerdem ist doch wohl lim b(k) = 0.
Also ist die Reihe q(k) konvergent, und das unendliche Produkt existiert somit.  |
    
Vredolf Ludrian (vredolf)

Mitglied
Benutzername: vredolf
Nummer des Beitrags: 29
Registriert: 03-2002
| | Veröffentlicht am Samstag, den 30. März, 2002 - 20:09: | 
|
Hi Zaph,
Etwas verspätet, aber doch noch: danke für den Tipp.
Dass aus b(k)->0 folgt, dass q(k) konvergiert kann ich
nachvollziehen. Nur nicht, wieso b(k)->0. Schließlich
gibt es doch beliebig große Lücken bei der Primzahl-
verteilung. Somit kann die nachfolgende Primzahl um einiges
größer sein, wodruch b(k) hier groß würde. Mir ist klar,
dass b(k) nicht über alle Schranken wachsen kann, da in jedem
Intervall [n;2n] stets eine Primzahl ist (Bertrand?).
Aber wieso ist lim[k->oo] b(k) = 0 ?
Wenn q(k) konvergiert, also q(k)=q, dann folgt ja problemlos
z.B.: e^q = lim[k->oo] pp(k) = pp (unser gesuchter Grenz-
wert).
Das bestimmen des Grenzwertes dürfte sich als das schwierigste
erweisen, falls überhaupt möglich !?
Anm.: Gemeint ist hier nicht eine Näherung auf beliebig
viele Dezimalstellen.
Gruß, VL |
    
marco i

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 31. März, 2002 - 11:30: | 
|
Hallo vredolf, habe eben gerade mal hier hereingeschaut.
Das scheint in der Tat eine schwierige Angelegenheit zu sein. Habe im Moment auch keine Lösung, aber zumindest zwei Anmerkungen:
1) Es ist wirklich nicht einzusehen, dass b(k) eine Nullfolge sein soll. Die Gründe hast du schon genannt. Die Sache mit dem Intervall [n;2n] müsste aber wohl eher [n;n!] heißen, oder?
2) Selbst wenn wir wirklich mal lim(b(k))=0 annehmen, stimmt die Argumentation von Zaph noch nicht. Eine alternierende Nullfolge impliziert noch lange keine konvergente Reihe, betrachte das Beispiel x(n) := (1+(-1)^n)/n. Die ist eine Nullfolge, aber die alternierende Reihe sum((-1)^n*x(n)) ist divergent. Zaph bezieht sich hier wohl auf das Leibnitzkriterium, dieses setzt aber eine "monoton fallende" Nullfolge voraus. Dies können wir bei der unregelmäßigen Verteilungen der Primzahlen mit Sicherheit nicht voraussetzen.
Das heißt zwar jetzt noch lange nicht, dass die Reihe divergiert, nur taugt die Argumentation halt nicht.
Ist aber ein sehr interessantes Problem!!!
marco i |
    
Vredolf Ludrian (vredolf)

Mitglied
Benutzername: vredolf
Nummer des Beitrags: 30
Registriert: 03-2002
| | Veröffentlicht am Sonntag, den 31. März, 2002 - 13:32: | 
|
Hi, marco i !
Sieh mal hier nach:
http://primes.utm.edu/glossary/page.php/BertrandsPostulate.html
Dort findest du obigen Satz nebst Beweis (den B. hab ich mir
noch nicht angesehen)
mfg, VL |
    
Zaph (zaph)

Fortgeschrittenes Mitglied
Benutzername: zaph
Nummer des Beitrags: 70
Registriert: 07-2000
| | Veröffentlicht am Sonntag, den 31. März, 2002 - 15:49: | 
|
Es scheint, dass ihr Recht und ich Unrecht habe. Asche auf mein Haupt! |
|