| Autor |
Beitrag |
    
Zaph (Zaph)

| | Veröffentlicht am Dienstag, den 17. April, 2001 - 15:58: | 
|
Beweise: Jede Gruppe von Leuten kann man so in Rote und Blaue aufteilen, dass jede rote Person mit geradzahlig vielen und jede blaue Person mit ungeradzahlig vielen roten Personen befreundet ist.
("Befreundet sein" ist hierbei eine symmetrische und irreflexive Relation. Das heißt, wenn A mit B befreundet ist, dann auch B mit A. Keine Person ist mit sich selbst befreundet.)
Scheint mir ziemlich knifflig zu sein. Hab' im Moment keine Idee ... |
    
Carmichael (Carmichael)

| | Veröffentlicht am Dienstag, den 17. April, 2001 - 16:46: | 
|
Folgendes ist mir noch nicht ganz klar:
"....jede rote Person mit geradzahlig vielen" roten,blauen oder Personen überhaupt befreundet ist?
blauen personen oder? |
    
Carmichael (Carmichael)

| | Veröffentlicht am Dienstag, den 17. April, 2001 - 17:18: | 
|
ach ne, rote natürlich, sonst gehts ja nicht immer, wenn jeder mit jedem befreundet ist. |
    
Zaph (Zaph)

| | Veröffentlicht am Dienstag, den 17. April, 2001 - 17:51: | 
|
Ja, jede rote Person soll mit geradzahlig vielen roten Personen befreundet sein. |
    
anonymius

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 15:58: | 
|
Was bedeutet "Gruppe von Leuten" genau? (Zahl, Eigenschaften?)und was ist mit 0 vorhandenen Blauen oder Roten?
z.B.:
2 Menschen, die miteinander befreundet sind.
Du kannst sie aufteilen und anmalen wie du willst, die Bedingungen sind nie erfüllt, es sei denn, beide wären blau.
Dann machen aber Bedingungen über die Freundschaft zu roten Personen keinen Sinn, wenn alle blau sind.
Oder das ist die Lösung:
Du malst immer alle blau an. |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 16:54: | 
|
Hallo Leute,
@ anonymius: Was eine Gruppe von Personen ist, ist doch wohl klar, oder?? Gemeint ist eine (beliebige) Ansammlung von Leuten, von denen einige (eventuell auch alle oder keine) miteinander befreundet sind.
0 ist selbstverständlich auch erlaubt. Bei zwei Personen, die befreundet sind, kann eine blau und die andere rot sein. Die rote ist dann mit 0 (gerade) roten und die blaue mit 1 (ungerade) roten Personen befreundet.
"Alle blau" funktioniert nicht, denn dann würde jede blaue Person 0 (gerade) rote Personen kennen.
Trotzdem befürchte ich, dass die Aufgabe falsch ist.
Hier der Original-Wortlaut:
10851 Proposed by David Beckwith, Sag Harbor, NY. Prove that any gathering of people may be devided into reds and blues in such a way that each red is acquainted with an even number of reds and each blue is acquainted with an odd number of reds. (Assume that acquaintance is a symmetric and irreflexive relation.)
Aber wie sieht's hiermit aus?

Punkte sollen Personen und Linien Freundschaften darstellen. Habe ich was übersehen?? |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 17:08: | 
|
Dann also so:
Personen: A, B, C, D, E, F
Freundschaften: A-B, A-C, B-C, C-D, D-E, E-B, B-F, C-F, D-F, E-F.
(Haus vom Nikolaus) |
    
Carmichael (Carmichael)

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 17:29: | 
|
ja so hab ich auch angefangen, mit punkten und verbinundgslinien! graphentheorie vielleicht?..
bin aber noch ned recht viel weiter gekommen. |
    
Carmichael (Carmichael)

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 18:08: | 
|
check mal
A,D,E,F rot
und
B,C blau
bei der Zeichnung steht nur image here..
ich ging also von den im Text erklärten Freundschaften aus. |
    
Zaph (Zaph)

| | Veröffentlicht am Mittwoch, den 18. April, 2001 - 19:55: | 
|
Jau stimmt! Diese Möglichkeit hatte ich tatsächlich übersehen.
Die Zeichnung hat nicht geklappt (obwohl et JPEG war), deshalb die verbale Erläuterung. |
    
Zaph (Zaph)

| | Veröffentlicht am Freitag, den 20. April, 2001 - 17:35: | 
|
Habe jetzt eine Möglichkeit gefunden, wie man die Menge der Roten ausrechnen kann. Diese Rechnung liefert ggf. auch als Ergebnis, dass es keine Lösung gibt. Es ist mir allerdings noch nicht gelungen zu zeigen, dass letzteres nie eintritt. |
    
Matroid (Matroid)

| | Veröffentlicht am Freitag, den 20. April, 2001 - 23:10: | 
|
Graphentheorie:
In einem Graphen ist die Anzahl der Ecken mit ungerader Valenz gerade.
Die Leute kann man sich als Eckenmenge eines Graphen vorstellen und bei "Freundschaft" gibt es eine Kante zwischen zwei Ecken.
Färbe in dem Graphen die Ecken mit gerader Valenz (Anzahl der Kanten an der Ecke) blau und die Ecken mit ungerader Valenz rot.
Nun bleibt noch das verwendete Ergebnis der Graphentheorie zu beweisen:
Beweis: Die Anzahl der Kanten sei n.
Jede Kante ist mit 2 Ecken inzident. Folglich ist die Summe der Valenzen aller Ecken gleich 2n, eine gerade Zahl!
Wenn es nun eine ungerade Anzahl von Ecken mit ungerader Valenz gäbe, dann wäre die Summe der Valenzen aller Ecken nicht gerade. Widerspruch.
Gruß
Matroid |
    
Matroid (Matroid)

| | Veröffentlicht am Freitag, den 20. April, 2001 - 23:19: | 
|
Aber beim zweiten Lesen der Aufgabe, sehe ich daß mehr verlangt ist. Sorry, bis später. |
    
Matroid (Matroid)

| | Veröffentlicht am Samstag, den 21. April, 2001 - 12:59: | 
|
Gibt es eine solche rot-blau-Färbung bei
 ? ? |
    
Matroid (Matroid)

| | Veröffentlicht am Samstag, den 21. April, 2001 - 13:00: | 
|
Gibt es eine solche rot-blau-Färbung bei
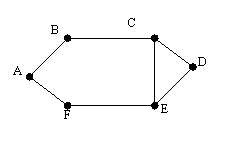 ? ? |
    
Carmichael (Carmichael)

| | Veröffentlicht am Samstag, den 21. April, 2001 - 21:11: | 
|
A,D rot
B,C,E,F blau |
    
Zaph (Zaph)

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 12:03: | 
|
So kann man die Menge der Roten ausrechnen:
Die Gruppe habe n Personen. Betrachte die (n x n)-Matrix A = (ai,j) mit ai,j = 1 falls Person i mit Person j befreundet ist und ai,i = 1 für i = 1,...,n. Dann ist A eine quadratische, symmetrische Matrix mit lauter Einsen in der Diagonale. In Matroids Beispiel sieht sie so aus:
| 1 | 1 | 0 | 0 | 0 | 1 | | 1 | 1 | 1 | 0 | 0 | 0 | | 0 | 1 | 1 | 1 | 1 | 0 | | 0 | 0 | 1 | 1 | 1 | 0 | | 0 | 0 | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | 1 | 1 |
wobei A Person Nr. 1, B Person Nr. 2, u.s.w. ist.
Sei nun b der n-dimensionale Vektor (1,1,...,1). Betrachte die Gleichung
xA = b
über Z2. (x ein n-dimensionaler Vektor). In Matroids Beispiel ist
x = (1,0,0,1,0,0)
eine (die einzige) Lösung des Gleichungssystems.
Es gilt nun:
Es gibt genau dann eine Aufteilung in Rote und Blaue, wenn das Gleichungssystem lösbar ist. Die Positionen des Lösungsvektors mit den Einsen geben die Roten an. In Matroids Beispiel also A und D.
Frage nun: Wieso ist das Gleichungssystem immer lösbar?? |
    
Matroid (Matroid)

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 19:12: | 
|
Danke für den Algorithmus, Zaph,
aber ich sehe ein Randprobleme.
a) Oft gibt es mehrere Lösungen. Wie kann man die mit dem Matrizenverfahren charakterisieren?
Beispiel: Graph K3, also 3 Ecken (A,B,C) und 3 Kanten.
Es gibt 4 Lösungen, nämlich (1,0,0) oder (0,1,0) oder (0,0,1) oder (1,1,1). Die letzte bedeutet, daß alle 3 Knoten rot gefärbt werden. Dann ist Dein b = (3,3,3). Das könnte man beheben, wenn man statt Ax=b nun Ax=l(1) verlangte. Aber das nur für ungerade l.
b) Sei G nun ein Graph mit den 4 Ecken A,B,C,D und den Kanten AB,BC,CD,DA (also ein Kreis der Länge 4).
Matrix:
(1 1 0 1)
(1 1 1 0)
(0 1 1 1)
(1 0 1 1)
Lösung (1, 1, 1, 1) [alle rot]
b=(3,3,3,3)
Wenn man mit b=(1,1,1,1) das Gl.system löst, kommt
x=(1/3,1/3,1/3,1/3)
Vielleicht kommt man ja bzgl. der Lösbarkeit des GlS weiter, wenn man die anderen möglichen (erlaubten) b in die Behauptung einbaut.
Gruß
Matroid |
    
Matroid (Matroid)

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 19:19: | 
|
Wenn man die Graphen über GF(2) repräsentiert, dann paßt Zaphs Lösungsverfahren anscheinend immer. Denn dann ist 1 + 1 + 1 = 1 usw. |
    
Zaph (Zaph)

| | Veröffentlicht am Sonntag, den 22. April, 2001 - 19:26: | 
|
Klar, GF(2) ist gemeint. Hatte ich aber geschrieben. GF(2) = Z2.
Dann sind alle vier Vektoren (1,0,0), (0,1,0), (0,0,1) und (1,1,1) Lösung von
(x1,x2,x3) A = (1,1,1)
mit
A =
|
    
Matroid (Matroid)

| | Veröffentlicht am Montag, den 23. April, 2001 - 18:13: | 
|
Hallo Zaph,
da müßte man doch mit LA was finden können.
Es gilt ja:
Das Gleichungssystem Ax=b hat genau dann mindestens eine Lösung, wenn rang(A) = rang(A,b).
Wenn rang(A) maximal, also gleich n ist, dann ist
rang(A) = rang(A,b) erfüllt.
Wenn der Rang nicht maximal ist, dann kann man das Gleichungssystem umformen zu (ungefähr):
A* =
und A* x = b*
Also eine Zeile besteht nur aus Nullen.
In diesem Fall kann man es vielleicht schaffen, die Lösung des ursprünglichen Problems auf die Lösung zweier Probleme mit weniger als n Ecken zurückzuführen (Induktion).
Oder hast Du das schon versucht?
Dazu benötigt man sicherlich noch ein graphentheoretisches Argument, weil die Matrix ja 'graphisch' ist und man das irgendwie ausnutzen muß.
Bei der Umformung des Gleichungssystem wird ja auch der Vektor b transformiert. Man muß dann zeigen, daß zu der Zeile mit Nullen (sei es die Zeile j) auch bj* = 0 ist.
Da bj=1 war, muß man also zeigen, daß die Anzahl der Umformungen (bis eine Zeile 0 ist) ungerade ist.
Was bedeutet es im Graphen, daß man eine Zeile der repräsentierenden Matrix zu 0 machen kann?
Ich vermute irgendetwas mit Kreisen und Kokreisen. Und dann gibt es noch den Satz, daß in Graphen für einen beliebige Kreis C und Kokreis D gilt
| C g D | ist ungerade. (g = geschnitten).
Meinst Du diese Denkrichtung bringt was? |
    
Zaph (Zaph)

| | Veröffentlicht am Montag, den 23. April, 2001 - 20:11: | 
|
Das algebraische Problem stammt zwar von einer graphentheoretischen Fragestellung, aber ich finde auch losgelöst davon ist dies nicht uninteressant. Schließlich kann man ja jede symmetrische Matrix mit Einsen in der Diagonale aus einem Graphen herbekommen.
Was ist ein Kokreis?
Zaph |
    
Matroid (Matroid)

| | Veröffentlicht am Montag, den 23. April, 2001 - 23:00: | 
|
Ein Kokreis eines Graphen G=(N,A) ist eine minimale Kantenschnittmenge. Eine Kantenschnittmenge ist eine Teilmenge D von A, so daß G'=(N,A-D) mehr Zusammenhangskomponenten hat als G.
Im Falle meines oben gegebenen Beispiels sind z.B. die Kantenmengen {AB,AF} und {CD,CE,AF} Kokreise, denn wenn man diese Kanten aus dem Graphen entfernt, entsteht ein Graph mit 2 Zusammenhangskomponenten.
In der Matrix-Repräsentation des Graphen kann man jede Zeile als eine Kantenschnittmenge lesen. Die erste Zeile obiger Adjazenz-Matrix lautet:
(1,1,0,0,0,1). Das entspricht dem Kokreis {AB,AF}.
Wenn man im linearen Gleichungssystem 2 Zeilen addiert, dann bildet man eine Linearkombination zweier Kantenschnittmengen.
Es gibt einen Satz: Jede Kantenschnittmenge ist die Vereinigung disjunkter Kokreise.
Aber mal abgesehen von Kokreisen, kann man das Gleichungssystem - im Falle, daß es nicht maximalen Rang hat - nicht auf eine Problem mit Rang minus 1 zurückführen? |
    
Zaph (Zaph)

| | Veröffentlicht am Dienstag, den 24. April, 2001 - 22:31: | 
|
Hi Matroid,
deinen Ideen mit den Kreisen/Kokreisen folgend habe ich mal versucht, den Fall zu betrachten, dass überhaupt keine Kreise existieren. Aber selbst da muss ich passen :-( |
    
Matroid (Matroid)

| | Veröffentlicht am Mittwoch, den 25. April, 2001 - 22:42: | 
|
Ich grüble auch noch nach einem möglichen Ansatz.
Einerseits in folgender Richtung:
Ich habe mich mir dem rang-Argument beschäftigt.
Also: wenn rang(A)=n gibt es eine eindeutige Lösung.
Wenn rang(A)<n, dann gibt es eine Linearkombination der Zeilenvektoren zi aus A mit:
Sn i=1 di * zi = 0
Wenn man nun zeigen könnte, daß Sn i=1 di gerade ist, dann folgt Sn i=1 bi = 0.
Also kann die erweiterte Koeffizientenmatric (A,b) zu einer Matrix (A',b') mit einer Zeile Nullen umgeformt werden. Sei i der Index dieser Zeile. Betrachte dann die Matrix A'', in der die i-te Zeile und Spalte gestrichen wird und in b' streiche den i-ten Wert (nenne das b'').
Dann bleibt ein Gleichungssysten A''x=b'' mit n-1 Zeilen und Spalten. Vielleicht ein Ansatz für Induktion?
Andere Denkrichtung:
Das zu-null-machen einer Zeile in der erweiterten Koeffizientenmatrix in graphentheoretische Begriffe übersetzen.
G=(V,A) sei im folgenden immer ein zsgh. Graph ohne Schleifen.
Ein Eckenkokreis ist die Menge aller Kanten, die mit einer Ecke inzident sind. Ein Eckenkokreis ist natürlich auch ein Kokreis.
Vermutung(?): Wenn die Matrix nicht maximalen Rang hat, dann existiert eine "gleichmäßig gerade" Überdeckung durch Eckenkokreise.
Eine "gleichmäßig gerade" Überdeckung ist eine nichtleere Menge von Eckenkokreisen D1, ... , Dk, sodaß Sk i=0 |{v}gD1| für alle Ecken v entweder 0 ist oder eine bestimmte positiv gerade Zahl.
Anschaulich: Für alle Ecken in G, die mit der Kokreisüberdeckung inzident sind, stimmt die Anzahl der Inzidenzen überein und ist gerade.
Dritter Ansatz: Wenn G eine Ecke mit Grad 1 hat, dann das Problem auf die Lösung des Problems mit n-1 Ecken zurückführen ...
Versuche zu beobachten, welche Grapheneigenschaften mit maximalem Rang zu tun haben.
Ansonsten:
Hinweise in Literatur? z.B. http://mat.gsia.cmu.edu/GROUP94/0796.html oder http://www.npac.syr.edu/techreports/hypertext/sccs-604/node4.html oder Computational and Graph Theoretic Aspects of Linear Algebra
Ich finde, Deine Aufgabe reicht für eine Dissertation.
Gruß
Matroid |
    
Zaph (Zaph)

| | Veröffentlicht am Donnerstag, den 26. April, 2001 - 21:41: | 
|
Jetzt hab' ich's wohl :-) Denn ich kann folgendes beweisen (alles über GF(2)).
Satz: Es sei A eine quadratische, symmetrische (n x n)-Matrix mit Diagonale d. Dann ist das Gleichungssystem Ax = d lösbar.
Hierzu überlege man sich:
Es seien i und j verschieden mit 1 <= i , j <=n.
A' gehe aus A hervor, indem zuerst Zeile Nr. i auf Zeile Nr. j von A und anschließend Spalte Nr. i auf Spalte Nr. j addiert wird.
d' gehe aus d durch Addition des i-ten Eintrags auf den j-ten Eintrag hervor.
Dann gilt:
1. A' ist symmetrisch.
2. Die Diagonale von A' ist d'.
3. Ax = d ist genau dann lösbar, wenn A'x = d' lösbar ist.
4. Das Gleichungssystem Ax = d lässt sich durch wiederholte Anwendung obiger Transformation in ein Gleichungssystem A''x = d'' verwandeln, wobei A'' eine Diagonalmatrix ist.
5. Wenn A'' eine Diagonalmatrix mit Diagonale d'' ist, dann ist A''x = d'' offenbar lösbar.
Ich hoffe, es stimmt alles. Sorry für diese Aufgabe.
Zaph. |
    
Matroid (Matroid)

| | Veröffentlicht am Donnerstag, den 26. April, 2001 - 22:45: | 
|
Die Aufgabe ist schon ok, keine Sorge.
Aber warum ist
Quote:
Ax = d ist genau dann lösbar, wenn A'x = d' lösbar ist.
?
Ich muß überlegen ....
Also die Multiplikation von A mit Elementarmatizen T von rechts und T-1 von links ergibt A' = T-1*A*T und das Ergebnis ist wieder eine Diagonalmatrix, stimmt!
Man kann die beidseitige Transformation auch auf die erweiterte Koeffizientenmatrix (A,d) anwenden.
Dann erhält man (A',d') (mit d wie Du schreibst) und der Rang(A',d')=Rang(A,d).
Ja, ich denke es stimmt.
Mach's gut
Matroid |
    
Zaph (Zaph)

| | Veröffentlicht am Samstag, den 28. April, 2001 - 12:06: | 
|
Ja, es stimmt wohl. Durch die Transformation (A,d) -> (A'.d') wird weder der Rang der Koeffizientenmatrix noch der Rang der mit der rechten Seite erweiterten Koeffizientenmatrix verändert. (Beachte: Zeilenrang = Spaltenrang.)
Zaph |
|