| Autor |
Beitrag |
    
Nadine

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 28. Oktober, 2007 - 11:28: | 
|
Hallo, ich habe keine Ahnung, wie ich an die Aufgaben herangehen soll:
Es sind folgende Mengen in einer komplexen Ebene gegeben:
a) A= z€C: 1-<Rez-<3; Betrag Im z-< Re z
b) B= z€C: 2-< Betrag z+1-2i<3
c) C= z€C: Betrag z+i-< Betrag z+1
d) D= z€C: Betrag z+3->5, Betrag z-<4
Diese mengen sollen gezeichnet werden.
Ich habe nicht die geringste Vorstellung, wie ich das machen soll. Vorher müssen ja bestimmt Berechnungen gemacht werden...
Könnte mir das jemand an einer mal als Beispiel erklären?
-< und -> soll übrigens "kleiner gleich" bzw "grösser gleich" bedeuten. (wusste nicht, wie ich das sonst schreiben soll)
Danke schon mal! |
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1273
Registriert: 08-1999
| | Veröffentlicht am Sonntag, den 28. Oktober, 2007 - 16:41: | 
|
Du wirst hoffentlich wissen, dass man aufgrund der Zweidimensionalität von C die Ebene zur Darstellung benötigt.
Man identifiziert also jeden Punkt (x,y) des IR2 mit der komplexen Zahl z=x+iy.
Wenn Du das nun in die einzelnen Bedingungen einsetzt, solltest Du Bedingungen für x und y erhalten (nicht notwendiger Weise getrennt!). Falls Dir die nicht auf Anhieb bekannt vorkommen, versuche Dir ein paar Punkte zu finden, die eine Lösung darstellen und taste Dich dann an den Rand des Lösungsbereichs heran.
Beispiel: |z|<1 <=> |x+iy|<1 <=> x²+y²<1
Die rechte Ungleichung stellt das Innere des Einheitskreises dar.
Übrigens: Das Kleiner-Gleich-Zeichen kannst Du durch den Befehle \ch{<=} erzeugen. |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 3292
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 28. Oktober, 2007 - 16:55: | 
|
a)das ganze Trapez 1,3,3+3i,1+i
b)bitte Klammern
c) findet man durch die Umformung
| z+i | / | z+1 | < 1
der Streifen zwische a+ai,a+(a+1)i
das "=" gilt für a + ai
d)
die Menge zwischen den durchgezeichneten Bögen
( der große Kreis, r=5, 3 nach rechts geschoben,
also z+3 repräsentiert Betrag > 5
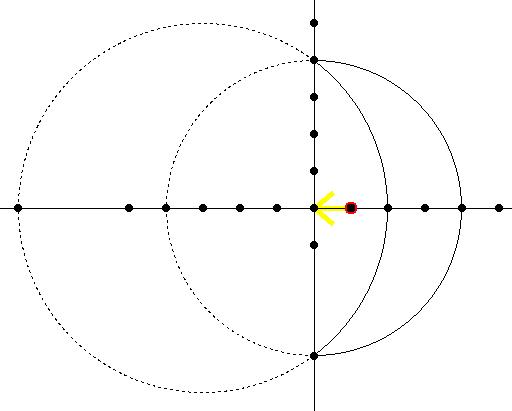
(die < und > sind durch \u{<} und \u{>}
erzeugt)
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Polya]
|
|