| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4427
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. September, 2004 - 16:21: | 
|
Hi allerseits

Die Aufgabe 471 nach dem Muster der Aufgabe
LF 470 , lautet:
Auf der x-Achse und auf der Geraden y = x sind je eine
unendliche Punktreihe definiert, die durch den Parameter t
miteinander gekoppelt sind.
Punktreihe P(t) auf x-Achse; Koordinaten von P: x = t, y = 0
Punktreihe Q(t) auf y = x; Koordinaten von Q: x = a+2*t ,y = a+2*t
(a ist eine von null verschiedene Konstante).
Gesucht wird eine Gleichung der von den Geraden
PQ eingehüllten Kurve.
Anmerkung
Die gegebenen Punktreihen sind ähnlich und nicht perspektiv.
Sie erzeugen beim genannten Verfahren eine Parabel als Enveloppe.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4428
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 22. September, 2004 - 17:52: | 
|
Hi allereseits

Man löse die Zusatzaufgabe:
Welche Steigung hat die Achse der Parabel, die sich in der
Aufgabe LF 471 ergibt?
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1607
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 22. September, 2004 - 20:35: | 
|
Hi megamath,
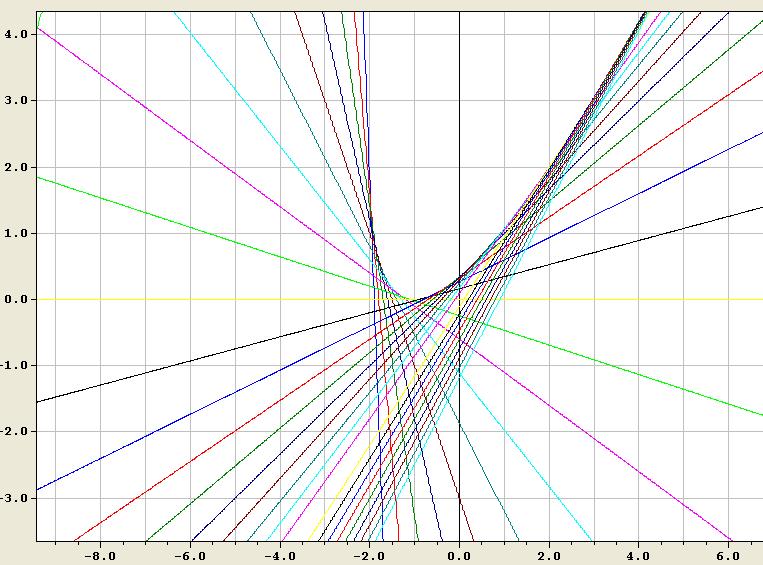
es entsteht diesmal eine gedrehte Parabel:
PQ : (a+2t)x - (a+t)y - (at+2t^2) = 0
PQ'(a) : 2x - y - a - 4t = 0
Daraus folt für die Enveloppe:
4x^2 - 4xy + y^2 + 4ax - 6ay + a^2 = 0
Hier führt man dann eine kleine aber feine Hauptachsentransformation durch, und sieht das es eine Parabel ist, bei Bedarf kann ich eine kleine Rechung nachliefern.
Als Achse erhalte ich:
y = 2*x + (7/5)*a
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4429
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 23. September, 2004 - 09:25: | 
|
Hi Ferdi

Vielen Dank für Deine Skizze; sie zeigt wiederum
das Wesentliche der Aufgabe.
Es wäre wohl hilfreich, wenn die Koordinatenachsen
und der Nullpunkt markiert würden zwecks Übersichtlichkeit.
Die Gleichung der Parabelachse ist richtig;
bemerkenswert: die Steigung ist unabhängig von a.
Wir freuen uns auf Deine kleinen Berechnungen!
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1609
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 23. September, 2004 - 14:21: | 
|
Hi allerseits , ,
hier meine kleine Rechung zur Bestimmung des Types des Kegelschnittes:
4x^2 - 4xy + y^2 + 4ax - 6ay + a^2 = 0
Wir betrachen die Eigenwerte der quadratischen Matrix:
Das charak. Polynom dieser Matrix lautet:
L( L - 5 ) = 0
die Eigenwerte also: L = 0 und L = 5.
L = 0 weißt daraufhin, das eine Parabel vorliegt!
Die Steigung m der Achse erhält man bei Parabeln über die Formel:
m = -B/C = 2
Nun habe ich t: y = -(1/2)x + b gesetzt, und bestimme b[ = -(3/10)*a ] so das diese Gerade und die Parabel nur einen gemeinsamen Punkt besitzen!
t ist dann die Scheiteltangente, und der Berührpunkt[ ( -(17/25)*a | (1/25)*a ) ] ist dann der Scheitel.
Man erhält dann auch die Gleichung der Achse: y = 2x + (7/5)*a
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4434
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 23. September, 2004 - 14:50: | 
|
Hi Ferdi

Vielen Dank für diese kompetente Herleitung!
Mit freundlichen Grüßen
H.R.Moser,megamath
|