| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4273
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 14. Juli, 2004 - 08:42: | 
|
Hi allerseits

Die Aufgabe LF 445 erscheint als Variante der Aufgabe LF 443
Wiederum sind fünf Punkte eines KS gegeben, nämlich:
P1 (2/-5), P2 (3/-1), P3 (-3/-1), P4 (-2/-6), P5 (0/0).
Wir wissen, dass diese fünf Punkte eine Ellipse eindeutig
bestimmen, und wir kennen ihre Gleichung; sie lautet:
44 x^2 - 23 xy + 81 y^2 - 23 x + 477 y = 0
Es soll zunächst ein einzelner sechster Punkt konstruiert
und berechnet werden.
Dieser Punkt liegt auf einem Strahl durch P5.
Wenn dies gelungen ist, drehen wir den Strahl um P5,
bestimmen für jede Lage den zusätzlichen sechsten Punkt
und erhalten so schliesslich alle Punkte des KS
und damit erneut seine Gleichung.
Bei der Lösung soll von der perspektiven Kollineation kein
Gebrauch gemacht werden; im Hintergrund ist hingegen
der Satz von Pascal wirksam.
Die einzelnen Schritte bei der Berechnung und Konstruktion
sind die folgenden:
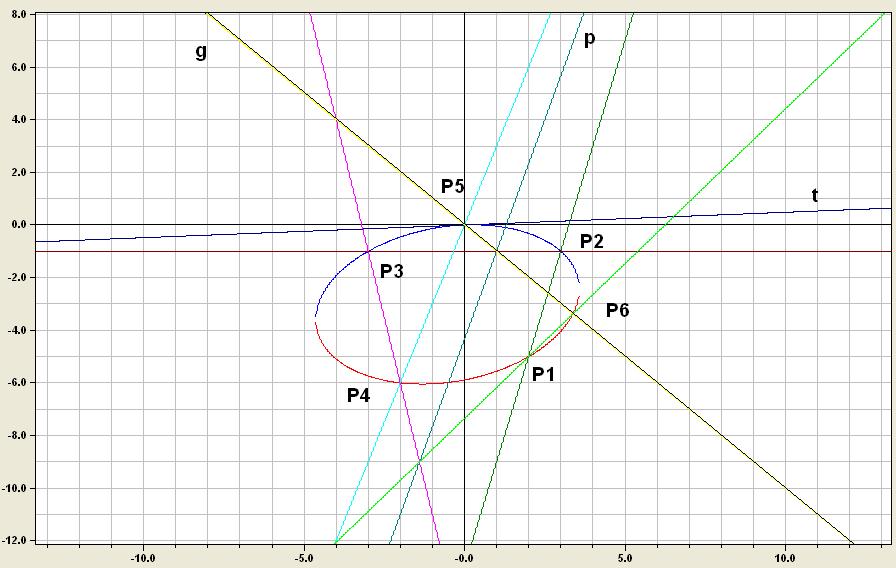
Q sei der Schnittpunkt der Geraden P1 P2 und P4 P5
Durch P5 wird eine beliebige Gerade g mit der Steigung m
gelegt (m wird die Rolle eines Parameters übernehmen).
Diese Gerade schneidet die Gerade P2 P3 im Punkt R.
Die Gerade QR ist die Pascalsche Gerade p.
Die Geraden p und P3 P4 schneiden sich im Punkt S.
Die Verbindungsgerade der Punkte S und P1 schneidet g
in einem sechsten Punkt P6 des Kegelschnitts.
Damit ist das Ziel erreicht.
Aufgaben im Einzelnen
a)
Man konstruiere für m = - 1 den Punkt P6
b)
Man berechne für m = - 1 die Koordinaten von P6
c)
Man berechne für einen allgemeinen Parameterwert m die
Koordinaten x und y des Punktes als Funktionen von m
d)
Man eliminiere im Ergebnis der Teilaufgabe c) den Parameter m.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1513
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 14. Juli, 2004 - 11:47: | 
|
Hi megamath,

also zeichnerisch komme ich zu:
P6 ( 3,4 / -3,4 )
Rechnerisch ist es:
P6 ( 125/37 | -125/37 )
Algemein mit dem Parameter m:
P6 ( [-477m + 23]/[81m^2 - 23m + 44] | [-477m^2 + 23m]/[81m^2 - 23m + 44 ] )
Nun hat man x und y in Abhängikeit von m, definiert man:
-477m + 23 = Z
81m^2 - 23m + 44 = N
x = Z / N ==> Z = x*N
y = mZ / N ==> Z = y*N / m
Gleichsetzen:
mx = y
m errechnet man aus der x-Koordinate, durch auflösen der quadratischen Gleichung in m(!):
m = [Z +- sqrt( Z^2 - 324x(44x - 23) )]/162x
Nun kann man auflösen und erhält nach Division durch 324:
44x^2 - 23xy + 81y^2 - 23x + 477y = 0
Kontrolle P6 € KS! Stimmt!
Auf Wunsch kann ich auch eine kleine Skizze für a) einfügen! Dann aber erst heute Abend nach der Arbeit!
mfg
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4274
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 14. Juli, 2004 - 13:48: | 
|
Hi Ferdi

Alle Deine Ergebnisse sind richtig; bravo!
Eine kleine Skizze ist sehr erwünscht und wird im Voraus verdankt!
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4275
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 14. Juli, 2004 - 13:49: | 
|
Hi allerseits

Zusatzaufgabe zu LF 445
Man berechne ohne Differentialrechnung die Steigung
der Ellipsentangente im Nullpunkt O.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1515
Registriert: 10-2002
| | Veröffentlicht am Mittwoch, den 14. Juli, 2004 - 22:36: | 
|
Hi megamath,

also ich habe es mir so gedacht mit der Tangente:
Ich nehme die Gerade g und bestimme m so, das g und die Ellipse nur einen gemeinsammen Punkt haben:
Man erhält die Gleichung:
x ( (81m^2 - 23m + 44)x - (23-477m) ) = 0
Die Klammer wir auch zum Punkt x = 0 für m = 23/477!
D.h. wir haben die Tangente t : y = 23/477*x! Ich habe sie auch in die Skizze mit aufgenommen! In der Skizze fehlt allerdings der Punkt Q (13/39), man kann ihn sich ja denken!
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4277
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 15. Juli, 2004 - 09:09: | 
|
Hi Ferdi

Deine kleine Skizze ist sehr eindrücklich; besten Dank!
Zur Steigung der Ellipsentangente in O:
Die Koordinatendarstellung der Ellipse mit m als Parameter lautet
nach unseren früheren Berechnungen:
x = [-477m + 23] / [ 81m^2 - 23m + 44 ]
y = [-477m^2 + 23m ] / [ 81m^2 - 23m + 44 ]
Setzt man dabei x = 0, so kommt aus der ersten Beziehung sofort
m = 23/477.
Anmerkung
Bei der Elimination von m kommt man ohne Auflösung
einer quadratischen Gleichung aus:
man setze m = y/x in die erste Gleichung ein, bearbeite den
Doppelbruch und dividiere beiderseits mit x; das geht:
dieser Wert ist nicht identisch null.
Die Ellipsengleichung schält sich dann von selbst heraus.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4278
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 15. Juli, 2004 - 10:36: | 
|
Hi Ferdi

Man kann die Zusatzaufgabe auch so lösen, wenn
man die Gleichung der Ellipse benützt:
Bekanntlich erhält man aus der allgemeinen Gleichung
zweiten Grades in x , y , d.h. aus
Ax^2+ 2Bxy + Cy^2 + 2Dx + 2Ey + F = 0
die Polarform:
x1(Ax+By+D)+y1(Bx+Cy+E)+(Dx + Ey +F) = 0
Die letzte Gleichung stellt die zum Punkt P1(x1/y1) als
Pol gehörende Polare p1 dar.
Liegt P1 auf dem KS, so ist p1 die Tangente mit P1
als Berührungspunkt.
In unserem Fall gilt:
A=44,B=-23/2,C=81,D=-23/2,E=477/2,F=0
x1=y1=0
Somit lautet die Gleichung der Tangente t in O:
-23 x +477 y = 0, daraus m = 23/477.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1522
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 15. Juli, 2004 - 22:41: | 
|
Hi megamath,
ich muss auch hier zugeben, das mir die Polarform für allgemeine KS-Gleichungen nicht geläufig war!
Ich wusste nur:
x^2 --> xx0
x --> (1/2)*(x + x0)
Aber der Term xy bereitete immer Schwierigkeiten! Diese dürften jetzt gelöst sein! Ich wollte dich schon Fragen, ob es sowas gibt, kam ich doch gestern bei dieser Aufgabe wieder auf das Problem "xy"...
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4282
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 16. Juli, 2004 - 08:48: | 
|
Hi Ferdi

Wenn ich in diesem Punkt gefordert werde, gehe ich ad hoc so vor:
Ich ermittle die Tangente der Kurve x y = 1 im Punkt
Po(xo/y0).
Aus y = 1/x folgt yo=1/xo oder xo yo =1
Ferner:
Die Steigung der Tangente ist m = - 1/xo^2,
ihre Gleichung demnach
y - yo = - 1/xo^2 ( x – xo ); beiderseits mit xo multipliziert gibt:
xo y – xo yo = - 1/xo x + 1, daraus
xo y = - 1/xo x + 2, schließlich:
xo y + yo x = 2, also
½ (xo y + yo x) = 1.
Jetzt wissen wir es!
Mit freundlichen Grüßen
H.R.Moser,megamath
|
|