| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4225
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. Juni, 2004 - 09:53: | 
|
Hi allerseits

Aufgabe LF 434
Es sollen nochmals Elemente des Bildes k´ eines Kreises k
bei gegebener Zentralkollineation konstruiert werden.
Gleichung des Kreises k : x^2 + (y – 3) ^ 2 = 4
Zentralkollineation:
Kollineationsachse e: y = 0 (x-Achse)
Kollineationszentrum Z (3 / 9)
Fluchtgerade v (1.Gegenachse): y = 7 (Parallele zur x-Achse)
Vorbemerkung:
Da die Gegenachse v den Kreis k meidet, ist das Bild k´ von k
eine Ellipse.
Die Aufgabe lautet:
a) Man konstruiere denjenigen Durchmesser P´Q´ der Ellipse,
welcher zur x-Achse parallel ist.
b) Man konstruiere den zu P´Q´ konjugierten Durchmesser
H´T´der Ellipse
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1478
Registriert: 10-2002
| | Veröffentlicht am Sonntag, den 27. Juni, 2004 - 10:16: | 
|
Hi megamath,

ich wollte mich nur für die nächsten Tage abmelden. Vielleicht zeichnet ja jemand anders auch gerne!
Ich werde in den nächsten Tagen auf dem Schützenfest bei mir im Dorf verweilen. Ein ganz besonderes Fest, wird unser Dorf doch 1150 Jahre alt!
Wenn du Lust hast kannst du ja mal schauen:
http://www.schuetzenbruderschaft-luechtringen.de
Ansonsten bis Mittwoch oder später...
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4226
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. Juni, 2004 - 17:20: | 
|
Hi Ferdi
  
Ich wünsche Erfolg und viel Vergnügen am Schützenfest!
Das trifft sich zeitlich insofern gut,
da ich in den nächset Tagen an
Prüfungssessionen teilnehme.
Auch hierbei kommt es auf gute Punktzahlen an.
Hoffentlich kann ich solche erteilen.
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4227
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. Juli, 2004 - 09:55: | 
|
Hi allerseits

Erste Hilfe für die Lösung der Aufgabe LF 434:
Man ermittle zuerst den Pol N der Gegenachse v
bezüglich k, indem man vom Schnittpunkt V
der y-Achse mit der Gegenachse die Tangenten
an k legt; die Verbindungsgerade p der
Berührungspunkte P und Q ist die Polare von V
und schneidet die y-Achse im gesuchten Pol N.
Ferner sei HT der auf der y-Achse liegende
Durchmesser des Kreises k, der Pol dieses
Durchmessers ist der unendlich ferne Punkt
der Kreissehne PQ; aus beiden werden
ausgewachsene konjugierte Durchmesser
der Ellipse!
Was wird passieren?
Bei der gegebenen zentralkollinearen Abbildung
geht N in den Mittelpunkt N´ der Ellipse über,
aus P und Q entstehen die Endpunkte P´, Q´
des ersten gesuchten Durchmessers.
Der zu P´Q´ konjugierte Durchmesser der Ellipse,
d.h. der zweite gesuchte Durchmesser, ergibt sich
durch Abbildung des Strecke HT.
Q sei der im ersten Quadranten liegende
Berührungspunkt der Kreistangente durch V.
Es ist zweckmäßig, mit Hilfe der Gegenachse v
und der Kollineationsachse e (x-Achse) das Bild m´
der Tangente m = V Q zu konstruieren.
H´T´ ist dann zu m´ parallel, da sich ihre Originale
HT und m im Punkt V auf der Gegenachse v
schneiden…………….
und so weiter und so fort.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4229
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. Juli, 2004 - 17:35: | 
|
Hi allerseits

Ein checkpoint:
Wo genau liegt der Bildpunkt Q´ des Punktes Q,
den ich in meinem letzten Beitrag definiert habe?
Man ist als geneigter Zeichner geneigt,
festzustellen, dass Q´ auf der y-Achse liegt.
Dem ist aber nicht so, hihi; es gilt :
die Koordinaten von Q´ lauten
xQ´~ 0,04 ; yQ = - 8/3.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1479
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 01. Juli, 2004 - 17:47: | 
|
Hi megamath,

erhält man die Steigung m' als ZS, wobei ich S so konstruiert habe: Die Tangente in Q schneidet die x-Achse in T, lege ich nun dort eine senkrechte Gerade an, so schneidet diese die Gegenachse im Punkt S!
Wenn das stimmt, will ich mal sehen, ob ich den Rest hinbekomme!
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4230
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. Juli, 2004 - 19:41: | 
|
Hi Ferdi

Aufpassen: Bei mir hat der Punkt T eine andere Bedeutung als bei Dir.
Die Tangente m in Q(sqrt(3)/4) an den Kreis k
schneidet die x-Achse in S (7/sqrt(3);0)
(nicht in T).
Zur Kontrolle :
Das Bild m´ hat die Steigng 2/3, da m´
parallell zu ZV verläuft.
Klar:
m und m´ schneiden sich auf
der Kollineationsachse in S.
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4231
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 02. Juli, 2004 - 07:27: | 
|
Hi allerseits

Eine weitere Hilfe:
Wir konstruieren das Bild q´ der y-Achse,
auf der der Kreisdurchmesser
H(0/1)T(0/5) liegt.
q´ geht durch den Nullpunkt und ist parallel zur
Geraden m´, Steigung 2/3.
Auf q´ liegen die gesuchten Endpunkte H´und T´
des zu P´Q´ konjugierten Durchmessers,
sowie der Mittelpunkt N´ der Ellipse.
Man findet diese Punkte mit Hilfe dreier
Kollineationsstrahlen durch H,T und N.
Daten:
H´(-1/2; -1/3)
T´(-15/2; -5)
N´(- 4 ; -8/3)
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1481
Registriert: 10-2002
| | Veröffentlicht am Freitag, den 02. Juli, 2004 - 15:56: | 
|
Hi megamath,

jetzt läuft wieder alles, hier meine Zeichnung, diesmal mit Beschriftung, ich hab gleich mal P' mit eingezeichnet, man sieht auch die Täuschung mit Q'...
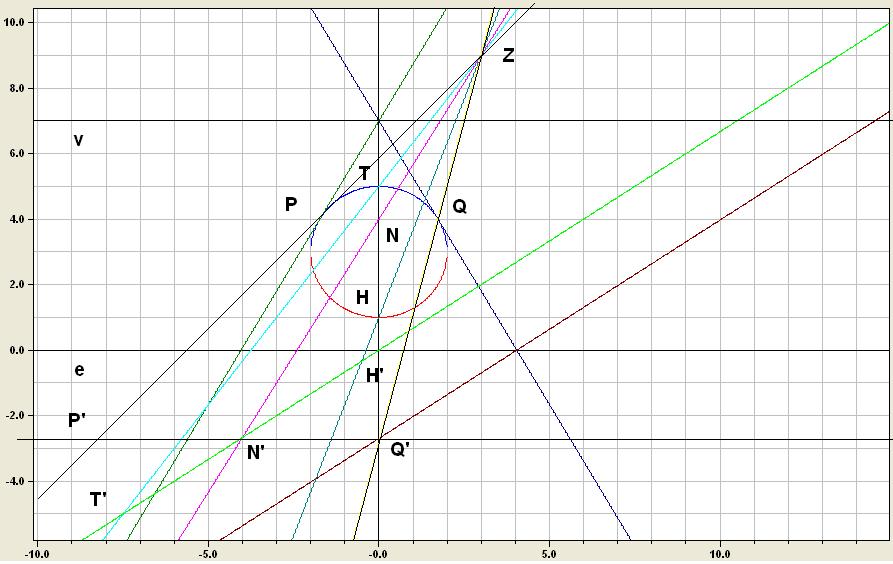
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4236
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 03. Juli, 2004 - 08:51: | 
|
Hi Ferdi,

Besten Dank für Deine Zeichnung!
Sie ist äußerst genau und hilft dabei,
die Konstruktionen nachzuvollziehen.
Viele „AHA-Erlebnisse“ wünscht
H.R.Moser,megamath
|