| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3768
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. April, 2004 - 10:50: | 
|
Hi allerseits

Eine willkommene Abwechslung:
Die Aufgabe LF 286 und die folgenden sind
den Integralen gewidmet!
Diese Aufgaben sollen grundsätzlich mit bestem Können
locker von Hand gelöst werden, also ohne Verwendung
von CAS und ohne Benützung irgendwelcher Programme.
Die Aufgabe LF 286 lautet:
Gegeben ist das (unbestimmte) Integral
J(n) = int [(cos x) ^ n dx ] ; n = 1,2,3….
Man leite eine Rekursionsformel für
J(n) her, indem J(n) durch J(n-2) ausgedrückt wird.
Benütze die Formel zur Berechnung von J(6).
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Tl198 (Tl198)

Senior Mitglied
Benutzername: Tl198
Nummer des Beitrags: 1233
Registriert: 10-2002
| | Veröffentlicht am Donnerstag, den 01. April, 2004 - 13:51: | 
|
Hi megamath,
schreib man:
cos(x)^n = cos(x) * cos(x)^(n-1)
Dann partielle Integration:
J(n) = sin(x) * cos(x)^(n-1) + (n-1)*int[sin(x)^2 * cos(x)^(n-2)]
Das Intgral kann umgeformt werden:
sin^2(x)*cos(x)^(n-2)
(1-cos(x)^2)*cos(x)^(n-2)
cos(x)^(n-2) - cos(x)^n
D.h. wir haben:
J(n) = sin(x)*cos(x)^(n-1) +(n-1)*J(n-2) - (n-1)*J(n)
J(n) = (sin(x)*cos(x)^(n-1))/n + (n-1)/n * J(n-2)
Das bringt für n = 6
cos(x)^6 = (sin(x)*cos(x)^5)/6 + (5/6)*J(4)
cos(x)^6 = (sin(x)*cos(x)^5)/6 + (5/6)*((sin(x)*cos(x)^3)/4 + 3/4*J(2))
cos(x)^6 = cos(x)^6 = (sin(x)*cos(x)^5)/6 + (5/6)*((sin(x)*cos(x)^3)/4 + 3/4*(sin(x)*cos(x)/2 + x/2))
Das kann man bestimmt noch zusammenfassen, oder mit Additionstheoremen umschreiben, aber das ist ja hier nicht gefordert 
mfg |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3769
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. April, 2004 - 14:07: | 
|
Hi Ferdi

Vielen Dank für die prompte und richtige Lösung.
Es geht weiter!
MfG
H.R.Moser,megamath |
    
Friedrichlaher (Friedrichlaher)

Senior Mitglied
Benutzername: Friedrichlaher
Nummer des Beitrags: 2113
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 01. April, 2004 - 15:25: | 
|
Hi, Megamath,
nicht
ganz das Einfache was Du wolltest,
aber
gleich eine "Endformel" für cosnx,
die
dann natürlich einfach integrierbar ist.
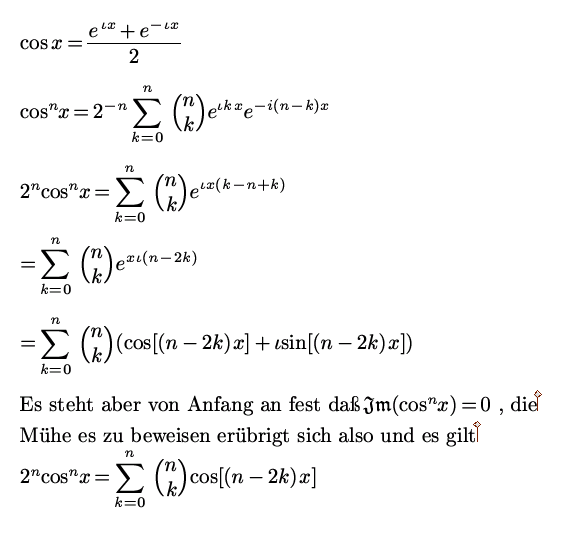
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3771
Registriert: 07-2002
| | Veröffentlicht am Donnerstag, den 01. April, 2004 - 15:43: | 
|
Danke Friedrich,

es ist natürlich sehr erwünscht,
möglichst viele Methoden kennen zu lernen!
MfG
H.R.Moser,megamath
|
|