| Autor |
Beitrag |
    
Redrunner (Redrunner)

Junior Mitglied
Benutzername: Redrunner
Nummer des Beitrags: 6
Registriert: 10-2003
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 10:19: | 
|
Hallo alle miteinander,
unser Prof. hat uns kurz in die elementaren Funktionen eingewiesen und meinte dann, nun können wir sein Aufgabenblatt lösen leider hab ich da so meine Probleme und selbst die Hilfe von mitstudierenden reicht zum lösen der folgenden Aufgabe nicht aus.
Ich hoffe nun hier einen Lösungsweg aufgezeigt zu bekommen.
Aufgabe: gesucht ist die Umkehrfunktion, definitionsbereich und Wertebereich der Folgenden Funktion:
y = x+1/x
Über schnelle Hilfe wäre ich sehr dankbar. |
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 898
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 13:51: | 
|
Hi!
Eine Funktion in der Form
y = f(x)
ist in expliziter Darstellung, weil y frei herausgerechnet ist.
Für die Umkehrfunktion sind die Variablen zu vertauschen:
x = f(y)
.. diese Darstellung heisst jetzt implizit, weil das y in einem Term "versteckt" ist. Wenn man dies wiederum explizit macht, also das y herausrechnet, erhält man die Umkehrfunktion in expliziter Form:
y = f^-1(x)
[das ^-1 ist keine echte Potenz, sondern nur eine symbolische Schreibweise, genauso gut kann für die Umkehrfunktion f*(x) schreiben]
Also:
Für die Umkehrfunktion vertauscht du zunächst die Variablen:
x = y + 1/y
Dadurch liegt bereits die Umkehrfunktion in impliziter Form vor, da ja das y nicht alleine steht. Wir lösen daher nach y auf (wir trachten eine Form y = .... zu erhalten, das ist die explizite Darstellung):
y² - xy + 1 = 0
quadr. Gleichung in y, nach y (!) lösen, x ist in diesem Moment als konstant zu betrachten.
a, b, c - Formel, a = 1, b = -x, c = 1
y1,2 = [x +/- sqrt((x² - 4)]/2
Wir erhalten zwei Funktionen, wobei wir uns nur für eine entscheiden dürfen, denn sonst würde keine Funktion vorliegen. Für eine Funktion ist Bedingung, dass einem x-Wert NUR EIN Funktionswert zugeordnet sein darf (eindeutige Zuordnung)!
Nehmen wir das positive Vorzeichen der Wurzel, so ist:
f^-1: x -> [x + sqrt((x² - 4)]/2
Über Definitions- und Wertebereich beider Funktionen unterhalten wir uns dann, wenn wir die Graphen betrachten können.
[wird fortgesetzt]
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 899
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 19:19: | 
|
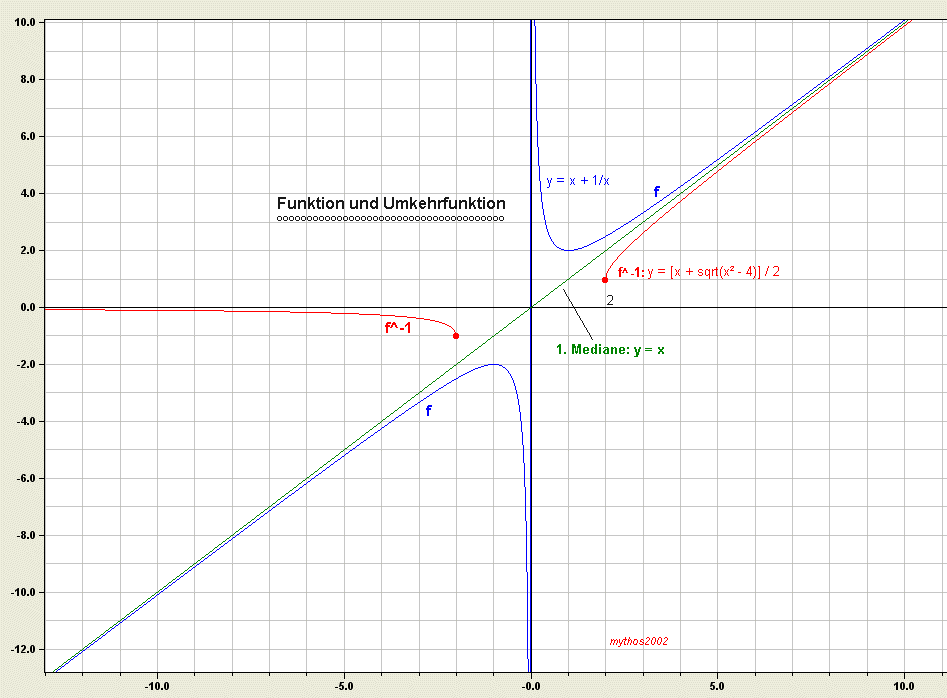
Nun die Grafik! Die blaue Kurve ist die gegebene Funktion, die rote die Umkehrfunktion.
Geometrisch ist der Zusammenhang dieser beiden Graphen gut zu erkennen: Der Graph der Umkehrfunktion entsteht durch Spiegelung des Graphen der gegebenen Funktion an der Winkelhalbierenden des 1. Quadranten (y = x, grüne Gerade).
[wird fortgesetzt]
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 900
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 20:22: | 
|
Die gegebenen Funktion
f(x) = x + 1/x
ist überall definiert, ausgenommen an jenen Stellen, an denen die Nenner allfälliger Brüche (bei gebrochen rationalen Funktionen) Null werden, denn die Division durch Null liefert keinen definierten Wert.
Wir erkennen leicht, dass die Definitionsmenge Df der Funktion
Df = R \ {0}
ist, R ist die Menge der reellen Zahlen.
Die Wertemenge Wf dieser Funktion sind alle Elemente von Funktionswerten f(x), die durch diese Funktion erreicht werden können, wenn man in die Funktion für x Elemente von Df einsetzt.
In unserem Fall ist Wf = {-oo <= f(x) <= -2 oder 2 <= f(x) <= oo}, es sind also alle Werte zwischen -2 und + 2 ausgeschlossen. Daher schreibt man auch
Wf = R \ {-2 < f(x) < 2}
Bei der Umkehrfunktion f^-1 wird zunächst Wf zur Definitionsmenge, Df^-1 = Wf. Die Wertemenge Wf^-1 muss nicht immer notwendigerweise Df sein, sie kann auch eine Teilmenge derselben sein, wie es im Beispiel auch der Fall ist.
Wir können dies bei der roten Kurve gut verfolgen! In Df^-1 ist der Bereich (-2 < x < 2) ausgeschlossen. Der Term sqrt(x² - 4) in f^-1 bestätigt dies auch, denn die Wurzel ist dann nicht reell, wenn x² < 4 bzw. |x| < 2 ist (dies entspricht -2 < x < 2).
Df^-1 = R \ {-2 < f^-1(x) < 2}
Die Wertemenge Wf^-1 ist hier tatsächlich nur eine Teilmenge von Df, denn sie reicht von +oo herunter nur bis einschließlich -1, außerdem ist 0 ausgeschlossen.
Wf^-1 = {-1 < f^-1(x) < 0 oder 0 < f^-1(x)}R
Beim Spiegeln an der 1. Mediane ist man versucht, die rote Kurve weiter zu zeichnen (zu vervollständigen), man könnte dies geometrisch auch ohne weiteres tun, bis sich die Kurven asymptotisch der x-Achse bzw. der 1. Mediane nähern. Es würden dann aber zu jedem x-Wert ZWEI "Funktionswerte" existieren, was aber der Definition der Funktion widerspricht. Daher muss man dort, wo die Tangente senkrecht steht (d. i. der Umkehrpunkt), den Graphen beenden.
Gr
mYthos
|
    
Mythos2002 (Mythos2002)

Senior Mitglied
Benutzername: Mythos2002
Nummer des Beitrags: 901
Registriert: 03-2002
| | Veröffentlicht am Mittwoch, den 28. Januar, 2004 - 21:03: | 
|
Wir haben in diesem Beispiel bis jetzt nur eine Lösung der quadratischen Gleichung berücksichtigt.
Man könnte meinen, dass das andere Vorzeichen bei der Lösung der quadratischen Gleichung nicht zugelassen ist. Das stimmt so nicht. Wir hätten ebenso gut auch mit der anderen Lösung ein konkretes Ergebnis erzielen können.
Es stellt also entweder die eine oder die andere Lösung eine Umkehrfunktion dar, aber eben nicht beide gleichzeitig.
Exakt gesehen muss man also die Vereinigung beider Lösungen, die getrennt voneinander je eine Funktion darstellen und die gleiche Definitionsmenge, aber nicht die gleiche Wertemenge besitzen, zur Umkehrfunktion zählen.
[Ende]
Gr
mYthos
|
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 771
Registriert: 11-2001
| | Veröffentlicht am Donnerstag, den 29. Januar, 2004 - 13:58: | 
|
Hallo,
Nimmt man die Aufgabenstellung wörtlich, so lautet
die Antwort : f besitzt keine Umkehrfunktion !
f ist nämlich nicht monoton, d.h.: die Abbildung
f : R-{0} ® R mit f(x) = x + 1/x
ist nicht injektiv. Damit f-1 existiert, muss man den
Definitionsbereich von f passend einschränken, z.B.
D = [1,¥[ oder D = ]-¥,-1].
mfG Orion
|
|