| Autor |
Beitrag |
    
Nadine (volkert)

Mitglied
Benutzername: volkert
Nummer des Beitrags: 16
Registriert: 07-2003
| | Veröffentlicht am Donnerstag, den 11. September, 2003 - 16:58: | 
|
Hallo weiß jemand von euch wie man von dem Term
Wurzel 3 *b + a die erste und die zweite Ableitung bildet? |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1414
Registriert: 02-2002
| | Veröffentlicht am Donnerstag, den 11. September, 2003 - 18:04: | 
|
 ja, weis jemand, ja, weis jemand,
wenn
Du noch sagst wie weit die Wurzel geht und
wonach
abgeleitet werden soll.
Aber
die anzuwendenden Regel sind
Potenzregel: (x^n)'= n*x^(n-1), für Quadratwurzel ist n=1/2
und die Kettenregel:
[f(g(x)]' = f'(g)*g'(x)
für die 2te Ableitung brauchst Du dann möglicherweise
auch
noch die Quotientenregel (f/g) = (f'g - fg')/g²
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|
    
Nadine (volkert)

Mitglied
Benutzername: volkert
Nummer des Beitrags: 17
Registriert: 07-2003
| | Veröffentlicht am Freitag, den 12. September, 2003 - 09:40: | 
|
Die Wurzel geht nur über die 3.
Die anzuwendeten Ableitungsregeln sind mir bekannt . Ich komm aber auf kein vernünftiges Ergebnis. Kannst du mir dabei helfen? |
    
Nadine (volkert)

Mitglied
Benutzername: volkert
Nummer des Beitrags: 18
Registriert: 07-2003
| | Veröffentlicht am Freitag, den 12. September, 2003 - 11:44: | 
|
Wurzel (3) *b+a .Es soll nach a abgeleitet werden.
Danke schon einmal für deine Hilfe! |
    
Friedrich Laher (friedrichlaher)

Senior Mitglied
Benutzername: friedrichlaher
Nummer des Beitrags: 1418
Registriert: 02-2002
| | Veröffentlicht am Freitag, den 12. September, 2003 - 12:22: | 
|
1te Ableitung: 1
2te Ableitung: 0
wenn
Du wirklich
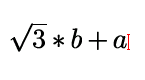
gemeint hast.
Wenn das Erlernen der Mathematik einigermaßen ihre Erfindung wiederspiegeln soll, so muß es einen Platz für Erraten, für plausibles Schließen haben.
[Aus dem Vorwort zu "Mathematik und plausibles Schliessen, Bd. 1 Induktion und Analogie in der Mathematik" von Georg Pólya]
|