| Autor |
Beitrag |
    
Jan

| | Veröffentlicht am Mittwoch, den 24. Mai, 2000 - 15:49: | 
|
Wie kann ich das Sehnenviereck mit folgenden Eigenschaften konstruieren?
a=6cm
c=5cm
alpha=100
beta=60
Danke und Gruss
Jan |
    
The Witch

| | Veröffentlicht am Donnerstag, den 25. Mai, 2000 - 12:05: | 
|
Hallo Jan,
hier deine Aufgabe mit einer Skizze, einer Zwischenkonstruktion und der Endkonstruktion. Alle Bezeichnungen beruhen auf den in der Schule üblichen Standardbezeichnungen für Vierecke. Da du nichts weiter dazu geschrieben hast, nehme ich mal an, dass diese auch für deine Aufgabe gelten. (Die in der Beschreibung verwendete Bezeichnung (AB) bedeutet Strecke AB. Die Bezeichnung g(BC') bedeutet Gerade durch B und C'.)
Skizze (die roten Stücke sind gegeben):
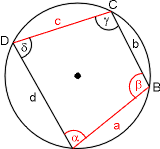
Zunächst einmal gilt der Satz:
In einem Sehnenviereck beträgt die Summe zweier gegenüberliegender Winkel stets 180°.
Es gilt also: a + g = 180° und b + d = 180°
Für dein Viereck ergibt sich daraus:
100° + g = 180° Þ g = 80°
60° + d = 180° Þ d = 120°
Konstruktionsbeschreibung:
- Zeichne die Strecke (AB) mit der Länge a = 6 cm. Trage in A an (AB) den Winkel a = 100° an. Trage in B an (AB) den Winkel b = 60° an.
- Wähle auf dem freien Schenkel von b einen beliebigen Punkt C'. Trage in C' an (BC') den Winkel g' = 80° an.
- Schlage um C' einen Kreis mit den Radius c = 5 cm. Der Kreis schneidet den freien Schenkel im Punkt D'. (Je nachdem, ob ihr das dürft, kannst du auch eine Strecke der Länge c = 5 cm mit dem Lineal auf dem freien Schenkel abtragen um D' zu bestimmen.)
Den Zustand nach diesen Konstruktionsschritten zeigt die folgende Zeichnung:
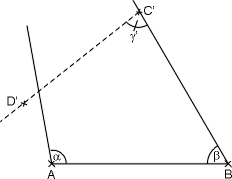
- Konstruiere nun die Parallele zu g(BC') durch D'. Sie schneidet den freien Schenkel von a im gesuchten Punkt D.
- Konstruiere die Paralle zu g(C'D') durch A. Sie schneidet den freien Schenken von b im gesuchten Punkt C.
Endkonstruktion:
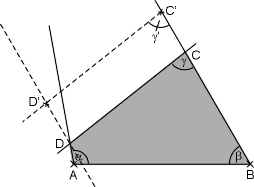
Das wars. Viel Vergnügen beim Nachvollziehen! |
|