| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4922
Registriert: 07-2002
| | Veröffentlicht am Freitag, den 25. März, 2005 - 14:10: | 
|
Hi allerseits

Sehr instruktiv ist die folgende Aufgabe;
man finde, wenn möglich, verschiedene
Lösungsmethoden.
In einer vierseitigen Pyramide sind alle Kanten
gleich lang.
Man ermittle die folgenden Winkel im Gradmass,
auf zwei Stellen nach dem Komma.
a)
den Winkel alpha zwischen einer Seitenkante
und der Grundfläche.
b)
den Winkel beta zwischen einer Seitenfläche
und der Grundfläche.
c)
den Winkel gamma zwischen zwei angrenzenden
Seitenflächen.
Gibt es eine plausible Erklärung für die
Relation
gamma = 2 beta ?
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4924
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 10:52: | 
|
Hi allerseits

Eine Präzisierung bezüglich der Lösungsmethoden
Die gestellte Aufgabe sollte nach Möglichkeit elementar gelöst werden.
Insbesondere sollte keine Vektorrechnung zur Anwendung kommen,
weder Skalarprodukt noch Vektorprodukt.
Für die Teilaufgaben a) und b) ist diese Einschränkung kein Problem.
Zur Lösung der Teilaufgabe c) fehlt mir hingegen noch eine taugliche Methode
für Anfänger im Fach Geometrie.
Ich nehme Lösungsvorschläge sehr gerne entgegen und danke im Voraus.
Mit freundlichen Grüssen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4925
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 11:15: | 
|
Hi allerseits

Hoffentlich hat man die Hieroglyphen
in meinen letzten Beitrag einigermassen
entziffern können; ein fremdsprachiger
Modus war noch wirksam.
MfG
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4926
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 13:37: | 
|
Hi allerseits

Die Aufgabe soll sukzessive gelöst werden.
Ohne Beschränkung der Allgemeinheit (oBdA)
dürfen wir die Länge einer Kante der Pyramide mit
s = 2 in Rechnung setzen.
Um die Idee zu fixieren, setzen wir die
Pyramide mit der Spitze S und den Ecken A,B,C,D der
Grundfläche in ein rechtwinkliges Koordinatensystem.
Die Ecken bekommen die folgenden Koordinaten:
A(1/-1/0),B((1/1/0),C(-1/1/0),D(-1/-1/0),S(0/0/sqrt(2).
M(1/0/0) ist der Mittelpunkt der Kante AB.
Lösung der Teilaufgabe a)
Im rechtwinkligen Dreieck AOS ist alpha der spitze Winkel bei A.
Unmittelbar folgt:
cos(alpha) = AO / AS = sqrt(2) / 2, also alpha = 45°
Lösung der Teilaufgabe b)
Im rechtwinkligen Dreieck MOS ist beta der spitze Winkel bei M.
Unmittelbar folgt:
cos(beta) = MO / MS = 1 / sqrt(3), also beta = 54,74°
Für cos(gamma) erhält man das Resultat
cos(gamma) = - 1/3, also gamma ~ 109,47°
Es gilt offenbar:
gamma = 2 * beta.
Dies soll in einem folgenden Beitrag nachgewiesen werden.
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4927
Registriert: 07-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 14:25: | 
|
Hi allerseits

Es ist einfach, mit Hilfe der Vektorrechnung den Winkel
gamma zu berechnen.
Auf Grund des im letzten Beitrag eingeführten Koordinatensystems
haben die beiden Seitenebenen ABS und ADS die folgenden
Koordinatengleichungen:
ABS: sqrt(2) x + z = sqrt(2)
ADS: sqrt(2) y - z = - sqrt(2)
n = {sqrt(2);0;1} ist ein Normalenvektor der Ebene ABS
m = {0; sqrt(2);- 1} ist ein Normalenvektor der Ebene ADS
Wir berechnen den Winkel gamma, der als Winkel dieser
Ebenennormalen erscheint, mit Hilfe des Skalarprodukts
und der Absolutbeträge dieser Vektoren:
cos (gamma) = - 1 / [sqrt(3) * sqrt(3)] = - 1 / 3,
wie vorausgesagt.
Die Hauptaufgabe besteht nun noch darin, den Winkel gamma
elementargeometrisch zu ermitteln.
Sind solche Methoden bekannt?
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 105
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 23:45: | 
|
Frohe Ostern!
 |
    
Elsa13 (Elsa13)

Erfahrenes Mitglied
Benutzername: Elsa13
Nummer des Beitrags: 106
Registriert: 12-2002
| | Veröffentlicht am Samstag, den 26. März, 2005 - 23:59: | 
|
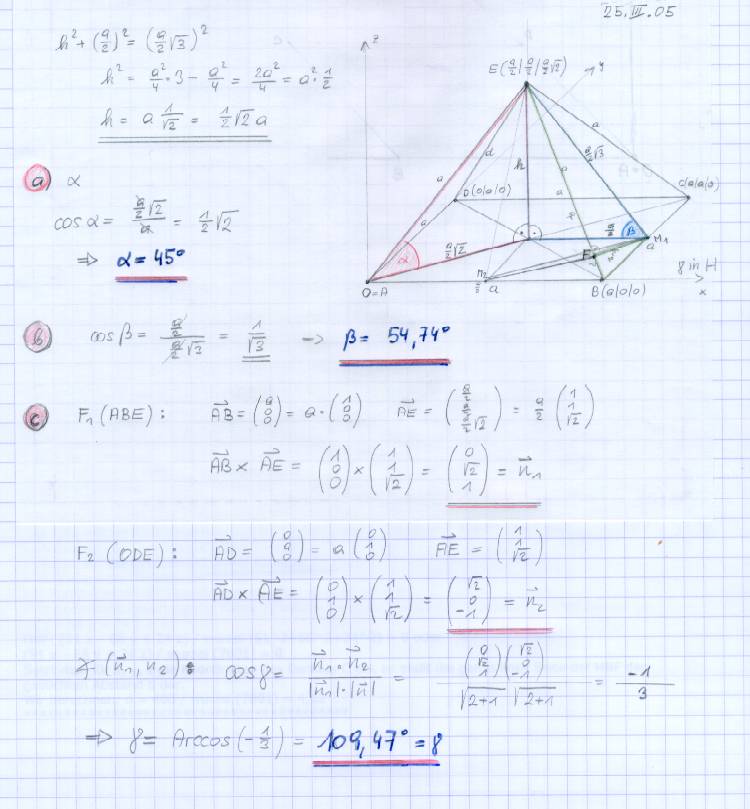
...nun ohne Vektorrechnung:
...
leider läßt sich das Bild nicht laden,
ich versuche es später wieder! |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4928
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 09:08: | 
|
Hi Elsa

Frohe Ostern!
Besten Dank für Deine Lösung mit dem Vektorprodukt samt Skizze.
Ich bin gespannt, wie c) elementar gelöst werden kann.
Ich habe unterdessen selbst eine Methode mit Einsatz der
Elemente der Darstellenden Geometrie gefunden, die mich aber
bloß zu ~ 70% befriedigt.
Ich führe sie heute oder morgen vor.
Mit freundlichen Grüßen
H.R. |
    
Ebi

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 09:30: | 
|
...in Vertretung von Elsa13 stelle ich ihre zweite Lösung zur Ansicht ins Forum.
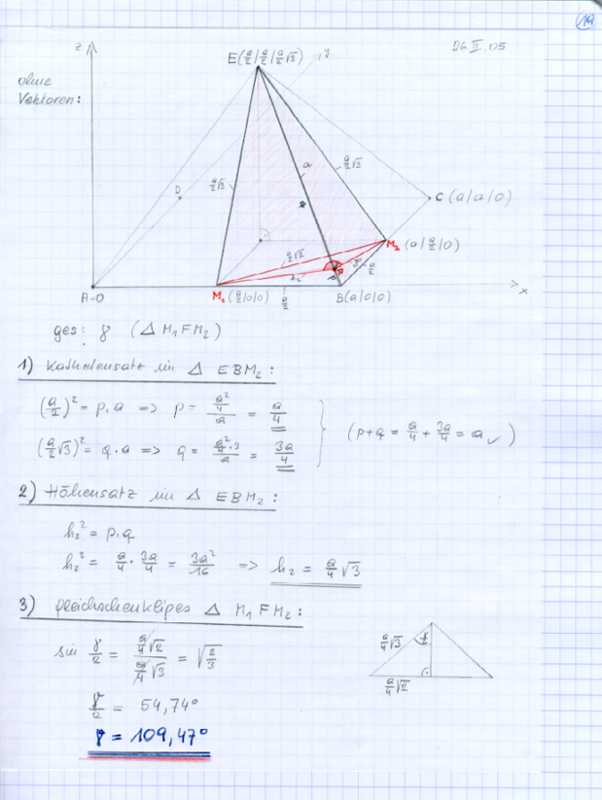 |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4929
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 10:27: | 
|
Hi elsa

Deine Lösung ist perfekt!
ich bin nun auf 100% gekommen.
Besten Dank!
Mit freundlichen Grüßen
HR |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4930
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 10:33: | 
|
Hi allerseits

Es folgt nun mein Versuch, die Teilaufgabe c) elementar zu lösen.
Um den Neigungswinkel zweier Ebenen E und F zu ermitteln, legt man eine so genannte Neigungswinkelebene N.
Diese steht zur Schnittgeraden s der beiden Ebenen in einem beliebigen Punkt P von s senkrecht; damit steht
N senkrecht zu jeder der beiden Ebenen.
N schneidet E in der Geraden g und F in der Geraden h,
die beide durch P gehen.
Die von P aus gehenden Strahlen auf g und h bilden
die Schenkel des Winkels phi der Ebenen E und F,
mit P als Scheitel.
Dieser Gedanke soll bei der vorliegenden Pyramide realisiert werden; wir behalten das Koordinatensystem, das in meiner
früheren Arbeit benützt wurde, bei, sodass das Folgende gilt:
Kantenlänge der Pyramide : 2 (Einheit cm)
Pyramidenspitze S, Ecken A,B,C,D der Grundfläche in einem rechtwinkliges Koordinatensystem:
Die Ecken bekommen die folgenden Koordinaten:
A(1/-1/0),B((1/1/0),C(-1/1/0),D(-1/-1/0),S(0/0/sqrt(2).
M(1/0/0) ist der Mittelpunkt der Kante AB.
Die (x,y)-Ebene soll als Grundrissebene verwendet werden.
Als Darstellungsmethode dient die so genannte kotierte
Normalprojektion, die mit einer einzigen Projektionsebene auskommt.
Punkte und Geraden in der (x,y)-Ebene werden mit
Hilfe des genannten Koordinatensystems
(mit z = 0) fixiert.
Wir stellen im Folgenden den Winkel phi der Ebene
ABS und der Ebene ASO live dar, sodass er in einem
rechtwinkligen Dreieck erscheint.
Als Resultat erhalten wir die Beziehung
cos (phi) =1 / sqrt(3).
Die Ebene ASO spielt dabei die Rolle einer Symmetrieebene.
Es gilt für den gesuchten Winkel gamma:
gamma = 2 * phi, sodass wiederum
cos (gamma) = - 1/3 herauskommt.
Fortsetzung folgt
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4931
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 12:59: | 
|
Hi allerseits

Im Folgenden soll nun der Winkel phi der Ebenen ABS und ASO
im wahrsten Sinn des Wortes in Erscheinung treten.
Wir legen die Neigungswinkelebene N, d.h. die zur Schnittgeraden k = AS der beiden Ebenen senkrechte Ebene, durch die Pyramidenspitze S.
Die Spur n von N , d.h. die Schnittgerade mit der (x,y)-Ebene,
steht senkrecht zur Projektion k´=AS´= AO von k und geht durch den Punkt Z(-1/1); dies als Anhaltspunkt für die Konstruktion der Spur n.
Diese Gerade n ist die diejenige Gerade, um die wir die Ebene N drehen wollen, bis sie mit der (x,y)-Ebene zusammenfällt.
Nach erfolgter Drehung um n als Achse erscheint der gesuchte Winkel phi in wahrer Größe.
Dieses Verfahren der Drehung um die Spur einer schiefen Ebene heißt Umklappung und darf nicht mit den Umlegungen projizierender Ebenen verwechselt werden.
Bei letzteren ist der Drehwinkel ausschließlich ein rechter Winkel.
Wie erhält man diesen Punkt Z?
Wir legen durch die Gerade AS die zur (x,y)-Ebene senkrechte
Ebene, die projizierende Ebene dieser Geraden.
Diese legen wir in die (x,y)-Ebene um, d.h wir drehen sie um um die Spur AO um 90°,bis sie mit der (x,y)-Ebene zusammenfällt.
Die umgelegte Kegelspitze S° fällt mit dem Punkt D
zusammen, also S°(-1/-1);es ist S´ S° = O S° = sqrt(2)
und k° = AS°, als Umlegung der Geraden k = AS
In der Umlegung erscheint der rechte Winkel zwischen k und der Fallgeraden f der Ebene N in S in wahrer Größe.
Daher legen wir durch S° die Senkrechte f° zu k°, welche n im gesuchten Punkt Z schneidet.
Damit ist Z definitiv bestimmt!
Es gibt eine weitere wichtige Spur, die Schnittgerade der Ebene ABS mit der (x,y)-Ebene!
Das ist die Gerade AB. Diese Spur e schneidet die Spur n von N im Punkt U(1/3); bitte genau kontrollieren!
Durch U läuft der eine Schenkel SU des gesuchten Winkels phi, durch Z der andere.
Wenn wir nun die Ebene N um n drehen und die Umklappung
vollziehen, so bleiben diese Punkte fest, der Scheitel S jedoch geht in den Punkt S* über, den wir sofort orten werden:
Wie erhalten wir die Umklappung S* von S?
S* liegt auf der Geraden OZ, im Abstand ZS° = 2 von Z
(nach außen).
Koordinaten von S*:
S*(-1-sqrt(2) / 1+sqrt2)
Schluss
Das Dreieck S*ZU ist bei Z rechtwinklig.
Katheten ZU = 2 sqrt(2) , ZS* = 2,
Hypotenuse 2 sqrt(3).
Der Innenwinkel bei S* ist der gesuchte Winkel
phi = ½ gamma
Für ihn gilt:
cos (phi) = 2 / [2 sqrt(3)] = 1 / sqrt(3); ENDLICH!
Mit freundlichen Grüßen
H.R.Moser,megamath |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 4932
Registriert: 07-2002
| | Veröffentlicht am Sonntag, den 27. März, 2005 - 19:26: | 
|
Hi allerseits

Es ist noch die am Anfang gestellte Frage zu beantworten:
„Gibt es eine plausible Erklärung für die
Relation
gamma = 2 beta ?“
Die Antwort ist frappant und entsprechend kurz.
Spiegelt man eine solche Pyramide, wie sie im Aufgabentext postuliert ist (alle Kanten sind gleich lang),
an der Ebene ABCD der Grundfläche,
so bilden Original S ABCD und Bild S´ABCD
zusammen ein reguläres Oktaeder.
Man erhält den Winkel gamma zweier angrenzender Seitenflächen, etwa den Winkel von SAB und S´AB, indem man den Winkel beta der Ebenen SAB und ABCD verdoppelt.
Mit freundlichen Grüßen
H.R.Moser,megamath. |
|