| Autor |
Beitrag |
    
anke

| | Veröffentlicht am Dienstag, den 05. Juni, 2001 - 11:37: | 
|
Einem Quadrat ABCD mit der Seitenlänge 10cm ist ein Reckeck PQRS einbeschrieben.
a) Wo muss der Punkt P auf der Seite AB gewählt werden, damit der Flächeninhalt des Rechtecks die Hälfe von dem Quadrat beträgt? (AP=a; PB= b)
b) Wie lang sind die Seiten u (Breite) und v (Länge) des Rechtecks?
Vielen Dank im voraus. |
    
Leo (Leo)

| | Veröffentlicht am Mittwoch, den 06. Juni, 2001 - 18:54: | 
|
Hm, ich wüsste jetzt nicht, wie man da rechnerisch ansetzt, muss da wirklich ein Recheck herauskommen? Denn der einfachste Fall ist hier ein einbeschriebenes Quadrat, a=b=5 und u=v=5*Ö2
Wenn es wirklich ein Rechteck sein soll, melde Dich nochmal |
    
Leo (Leo)

| | Veröffentlicht am Mittwoch, den 06. Juni, 2001 - 19:14: | 
|
Ich habe mir mal so ein paar Formeln aufgeschrieben:
Es gilt:
u*cos(alpha)=a
v*cos(90-alpha)=10-a
und, damit es wirklich einbeschrieben wird:
b*sin(alpha) + l*sin(90-alpha)=10
Mach dir eine Zeichnung, vielleicht kannst Du es nachvollziehen, wie ich drauf komme.
auf jeden Fall komme ich schon dadurch, ein Rechteck einschreiben zu wollen auf dies:
u*sin(alpha)+v*(cos(alpha)=10
v*sin(alpha)+u*(cos(alpha)=10
aus diesen beiden Gleichungen folgt: b=l,
also landen wir automatisch beim Quadrat, man kann also kein Rechteck einbeschreiben, falls ich richtig gerechnet habe, ich denke schon |
    
Lerny

| | Veröffentlicht am Donnerstag, den 07. Juni, 2001 - 09:07: | 
|
Hallo Anke
hier mein Versuch
Zuerst mal eine Skizze
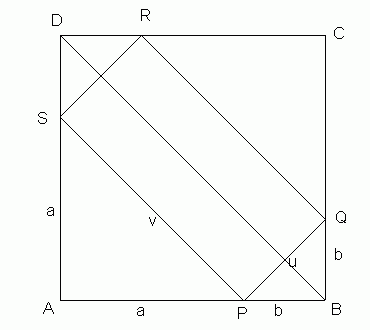
Es gilt u²=a²+a²=2a² und v²=b²+b²=2b² und damit
u=aÖ2 und v=bÖ2
Wegen a+b=10 folgt a=10-b und damit
u²=2(10-b)²=> u=(10-b)Ö2
Der Flächeinhalt des Quadrats beträgt 10²=100cm²; also muss der Flächenhalt des Rechtecks 50cm² sein.
Mit der Formel für den Flächeninhalt eines Rechtecks folgt nun:
A=u*v=(10-b)Ö2*bÖ2
A=2b(10-b)=50
20b-2b²=50
2b²-20b+50=0 |:2
b²-10b+25=0
(b-5)²=0
b=5
a=10-b=10-5=5
b) u=(10-b)Ö2=(10-5)Ö2=5Ö2
v=bÖ2=5Ö2
Damit ist das gesuchte Rechteck ein Quadrat.
mfg Lerny |
    
Leo (Leo)

| | Veröffentlicht am Donnerstag, den 07. Juni, 2001 - 15:10: | 
|
Hm, jetzt geht mir ein Licht auf, natuerlich kann man ein Rechteck einbeschreiben, wobei alpha=45 Grad. Sein muss. Daher muss ich jetzt ueberdenken, wo bei meinen Berechnungen der Fehler ist, denn laut meinen Angaben kann man gar kein Rechteck einbeschreiben. Also auf ein Neues. Aber dass das Ergebnis ein Quadrat sein muss, ist klar. |
    
Leo (Leo)

| | Veröffentlicht am Donnerstag, den 07. Juni, 2001 - 15:23: | 
|
Jetzt ist mir eines klar geworden, da der sinus und der cosinus bei 45Grad gleich sind, gilt in meiner Formel u+v=10*Wurzel(2)
also gilt u`2-10*Wurzel(2)*u+50=0 (Flaeche = 50)
also u=5*Wurzel(2) und dementsprechend a=5
=> Die Loesung ist ein Quadrat.
Danke fuer den Anstoss, Lerny, jetzt muessen wir nur noch hoffen, dass Anke unsere beiden Ansaetze verstanden hat.Vor allem, warum man ein Rechteck nur einbeschreiben kann, wenn es parallel zur Diagonalen liegt. Wenn man das hat, ist der Rest nur noch "Formeln einsetzen"mit Pythagoras. |
    
Anke

| | Veröffentlicht am Freitag, den 08. Juni, 2001 - 16:51: | 
|
Vielen Dank! Ich drucke das gleich aus und wenn ich noch Fragen habe, melde ich mich noch mal! |
|