| Autor |
Beitrag |
    
Eviii (Eviii)

Erfahrenes Mitglied
Benutzername: Eviii
Nummer des Beitrags: 64
Registriert: 05-2003
| | Veröffentlicht am Freitag, den 21. Januar, 2005 - 20:12: | 
|
Zur Zeit hänge ich an einer Übungsaufgabe,
Finde eine stetige Funktion von f:R nach R für die gilt f(x)=c für alle c genau drei Lösungen hat.
eine Funktion die schon ziemlich nah an das rankommt ist f(x)= 1/sqrt(2) *x + sin(x)
hat leider nur eine Nullstellt 1/1.4665*x war ne ziemlich gute Näherung, bloß eine genaue Lösung ist ja gesucht.
Vielen Dank
eviii |
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1053
Registriert: 08-1999
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 20:04: | 
|
Ich persönlich würde es ja einfach abschnittweise versuchen. Ausgehend von einer Funktion dritten Grades mit zwei Extremen, die zwischen den Extrema ja jeden Wert dreimal annimmt, setzt man diese Funktion stetig fort bis man unendlich viele Abschnitte mit dieser Eigenschaft erhält.
Nachdem ich mir die von Dir vorgeschlagene Funktion geplottet habe und mit 2/9*x+sin(x) eine "bessere" Funktion ermittelt habe, bin ich noch zu folgender Idee gelangt:
Setze die Funktion mit f(x)=ax+sin(x) an und sorge durch Ableiten dafür, daß ein Maximum stets auf Höhe des übernächsten Minimums liegt. Aufgrund der Punktsymmetrie genügt es sogar zu fordern, daß das "erste" Minimum eine Nullstelle sein soll. |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1094
Registriert: 05-2002
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 20:29: | 
|
Was bitte soll gefunden werden?
f(x) = c <-- das ist doch eine Konstante Fkt. und die hat nur für c = 0 überhaupt eine Nullstelle, und da halt unendlich viele;

Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1054
Registriert: 08-1999
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 20:59: | 
|
@Mainzi:
Es geht darum eine Funktion zu finden, die jeden reellen Wert genau dreimal annimmt. |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1095
Registriert: 05-2002
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 22:02: | 
|
Danke Ingo,
was ist davon zu halten:
für positive x
f(x) = [x] + 1/2 - 1/2 * cos( 3pi * ( x - [x] ) )
und gesamt
f(x) = sign(x) * ( [|x|] + 1/2 - 1/2 * cos( 3pi * ( |x| - [|x|] ) ) )
cos( 3pi * ( x - [x] ) ) hat im Intervall der Breite 1 genau 1,5 Perioden; [x] ist die Gaußklammer
für positive x würds dann so aussehen:
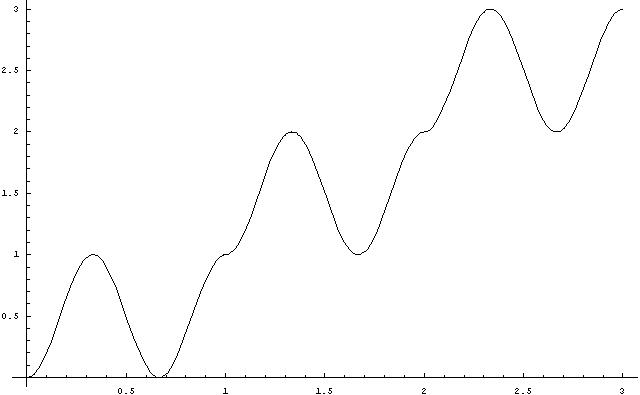
Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1055
Registriert: 08-1999
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 22:47: | 
|
Sieht recht gut aus wobei ich mir bei der Stetigkeit noch nicht so sicher bin. Grafisch scheint sie gegeben zu sein, aber da die Gaußklammerfunktion Sprungstellen hat, müsste man diese noch näher beleuchten denke ich. |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1096
Registriert: 05-2002
| | Veröffentlicht am Samstag, den 22. Januar, 2005 - 23:32: | 
|
Stimmt, die Gaußklammer ist sehr sprunghaft;
f(x) = [x] + 1/2 - 1/2 * cos( 3pi * ( x - [x] ) )
wobei man stellt sehr schnell fest, daß eine diffbare Fortsetzung ist;
an der Stelle 1 von links kommend gilt:
0 + 1/2 - 1/2 * cos( 3pi * ( 1 - 0 ) ) = 1/2+1/2 = 1
an der Stelle 1 von rechts kommend gilt:
1 + 1/2 - 1/2 * cos( 3pi * ( 1 - 1 ) ) = 1+1/2-1/2 = 1
damit passt des,
und wenn man genau schaut sieht man, daß es sich nur um horizontale Wendetangenten handeln kann bei diesen Stellen, an denen die Gaußklammer springt; das Maximum vom rechten Rand des Intervalls deckt sich mit dem Minimum des linken Randes des Folgeintervalls;

Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 967
Registriert: 11-2001
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 08:38: | 
|
Hallo,
wie wäre es mit
f(x) = [x/p-1/2] + sin(x) <=>
f(x) = n + sin(x)
für (2n+1)x/p£ x < (2n+3)x/p ,
n€ Z ?
mfG Orion
|
    
Orion (Orion)

Senior Mitglied
Benutzername: Orion
Nummer des Beitrags: 968
Registriert: 11-2001
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 10:08: | 
|
Hallo,
Variante :
Definiere x® zack(x) , x€[0,1[ , durch
zack(x) := 3x für 0£ x < 1/3,
zack(x) := 2-3x für 1/3£ x < 2/3,
zack(x) := 3x-2 für 2/3 £x < 1.
Sei dann
f(x) := zack(x-[x]) + [x].
mfG Orion
|
    
Eviii (Eviii)

Erfahrenes Mitglied
Benutzername: Eviii
Nummer des Beitrags: 65
Registriert: 05-2003
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 13:19: | 
|
Erstmal vielen Dank für eure Hilfe,
an die Stetige Fortsetzung des Kosinus hab ich auch schon gedacht(da es ja auf den Blatt hauptsächlich um Kosinus und Sinus geht).
Bei der stetigen Fortsetzung, von einem Polynom dritten Gerades: Die Stetigkeit folgt dann durch Punktsymmetrie.
a*x+sinx und Ableiten und Gleichsetzen kommt bei mir nur sinnloses unstetiges Zeug raus, das hab ich aufgegeben.
Bei der Funktion Zack wird es mir wohl am leichtesten sein Stetigkeit nach zu weisen.
Ich hatte mich nicht getraut solche Zacken zu machen, weil ich dachte, diese Funktionen sind nicht stetig. Ich vermische den Begriff immer mit differenzierbar.
Ciao
Evi |
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1057
Registriert: 08-1999
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 19:23: | 
|
Nach wie vor stört mich die Tatsache, daß mit der Gaußklammerfunktion eine unstetige Funktion verwendet wird, auch wenn das Endergebnis richtig. Ich denke aber es müsste eine einfachere Lösung geben.
Ich habe deshalb weiter an dem Ansatz f(x)=ax+sin(x) beschäftigt.
f'(x)=a+cos(x)
erstes Minimum liegt bei x=2*pi-arccos(a)
Dies muss eine Nullstelle sein, um zum Erfolg zu kommen.
f(2*pi-arccos(a)) = a*(2*pi-arccos(a)) + sin(2*pi-arccos(a)) = 0
<=> a*(2*pi-arccos(a)) + sin(2*pi-arccos(a)) = 0
<=> a*(2*pi-arccos(a)) - sin(arccos(a)) = 0
<=> a*(2*pi-arccos(a)) - Wurzel(1-a²) = 0
=> a²((2*pi-arccos(a))²+1) = 1
Und hier setzen die Probleme ein. Ich habe mir zunächst damit geholfen für arccos(a)=pi/2 anzusetzen, wobei das recht ungenau ist.
a²((2*pi-pi/2)²+1) = 1
a = sqrt(1/(9*pi²/4+1)) = sqrt(4/(9*pi²+4)) = 2 / sqrt(9*pi²+4) = 0,2076
Das Ergebnis ist respektabel, aber leider nicht genau genug. Genauer wäre es mit einer Linearisierung arccos(x)=pi/2-x, aber halt immer noch nicht exakt. (Und führt bereits auf eine Gleichung 4.Grades).
Hat jemand eine bessere Idee, oder ist das Unterfangen tatsächlich hofnungslos? |
    
Christian_s (Christian_s)

Senior Mitglied
Benutzername: Christian_s
Nummer des Beitrags: 1716
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 22:57: | 
|
Hallo Ingo
Ich habe mir gerade mal deine Funktion in Maple plotten lassen mit a=0,2076. Es scheint so als läge das erste Minimum unter Null. Damit gäbe es aber rechts von 0 zwei Nullstellen. Insgesamt hätte man wegen der Punktsymmetrie der Funktion also 5 Nullstellen, was ja nicht sein darf. Vielleicht kann man mit dem Ansatz f(x)=a*x+sin(x) gar nicht zum Ziel kommen?!
MfG
Christian |
    
Christian_s (Christian_s)

Senior Mitglied
Benutzername: Christian_s
Nummer des Beitrags: 1717
Registriert: 02-2002
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 23:22: | 
|
Hallo nochmal
Ist natürlich Blödsinn was ich oben geschrieben habe. Man wählt a ja gerade so, dass die Funktion beim ersten Minimum eine Nullstelle hat.
Mfg
Christian |
    
Mainziman (Mainziman)

Senior Mitglied
Benutzername: Mainziman
Nummer des Beitrags: 1101
Registriert: 05-2002
| | Veröffentlicht am Sonntag, den 23. Januar, 2005 - 23:23: | 
|
Hi ihr,
die Bedenken mit der Gaussklammer sind nicht von der Hand zu weisen; aber das ist ja das schöne daran, daß das Maximum mit dem Minumum des nachfolgenden Intervalls zusammenfällt und somit eine horiz. Wendetangente ergibt, auch wenn man die 2te Ableitung in dem Punkt gar nicht machen kann *gg*
Noch was: diese Punkte stellen "Knackpunkte" einer Punktsymetrie dar;
die Variante mit zack(x) gefällt mir sehr gut,
einfach und bis auf die Knickstellen vollständig diffbar (diese sind nur stetig);

Mainzi Man,
ein Mainzelmännchen-Export,
das gerne weiterhilft
oder auch verwirren kann *ggg*
|
    
Ingo (Ingo)

Moderator
Benutzername: Ingo
Nummer des Beitrags: 1058
Registriert: 08-1999
| | Veröffentlicht am Montag, den 24. Januar, 2005 - 01:51: | 
|
Wie ich oben schon sagte: Die Lösung mit der Gaußklammer ist völlig korrekt.
Ich gehe aber mit meinem Ansatz einen Schritt weiter und suche eine beliebig oft differenzierbare Funktion. Theoretisch ist es möglich sie mit dem Ansatz zu bekommen, praktisch gibt es aber anscheinend unüberwindbare Rechenprobleme. Oder hat noch jemand eine Idee oder einen anderen Vorschlag? |