| Autor |
Beitrag |
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3093
Registriert: 07-2002
| | Veröffentlicht am Dienstag, den 25. November, 2003 - 16:22: | 
|
Hi allerseits

In der Aufgabe LF 114 soll die Bernoullische Ungleichung
(1+p) ^ n > 1 + n p
für natürliche Zahlen n>1 und positive p mit Hilfe des Satzes vom
arithmetischen / geometrischen Mittel bewiesen werden.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Martin243 (Martin243)

Senior Mitglied
Benutzername: Martin243
Nummer des Beitrags: 904
Registriert: 02-2001
| | Veröffentlicht am Mittwoch, den 26. November, 2003 - 10:57: | 
|
Hi!
Ich erhebe keinen Anspruch auf die eleganteste Lösung, aber die sollte es auch tun:
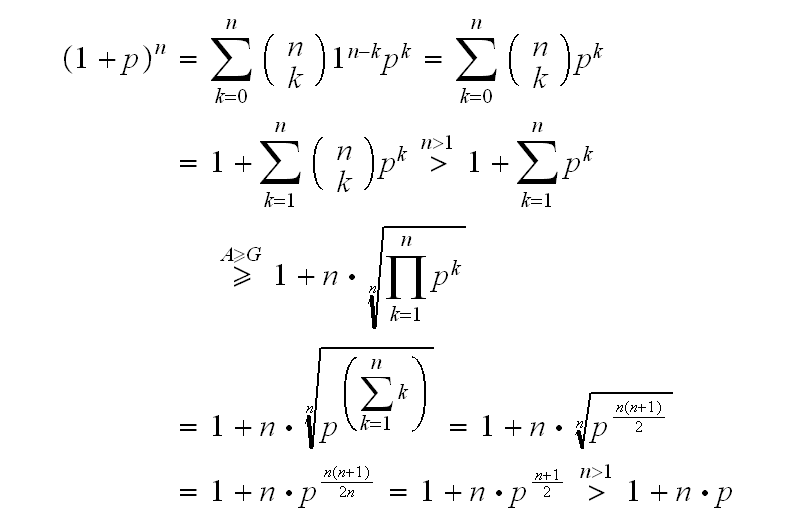
MfG
Martin
________
Die Natur spricht die Sprache der Mathematik:
Die Buchstaben dieser Sprache sind Dreiecke, Kreise und andere mathematische Figuren.
Galileo Galilei
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3097
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 26. November, 2003 - 11:04: | 
|
Hi Martin

Bravo, Deine Lösung gefällt mir sehr gut,
sie hat Substanz!*
Ich zeige dir meine L. etwas später,als
Pop-Variante.
MfG
H.R.Moser,megaamth
|
    
Megamath (Megamath)

Senior Mitglied
Benutzername: Megamath
Nummer des Beitrags: 3098
Registriert: 07-2002
| | Veröffentlicht am Mittwoch, den 26. November, 2003 - 11:07: | 
|
Hi allerseits

Lösung der Aufgabe LF 114.
Mit etwas Raffinement kann die verlangte
Brücke gebaut werden:
Sei a1 = 1 + np > 0 , a2 = a3 =….= an = 1.
Berechnung des arithmetischen Mittels A der aj:
A = 1/n [1+np +(n-1)*1] = 1/n [1+np+n-1] =1+p.
Berechnung des geometrischen Mittels G der aj:
G ^ n = (1+n p)*1*1…*1 = 1 + n p
Setze an: A > G - > (1 + p) ^ n > 1 + n p , qed.
Mit freundlichen Grüßen
H.R.Moser,megamath
|
    
Martin243 (Martin243)

Senior Mitglied
Benutzername: Martin243
Nummer des Beitrags: 905
Registriert: 02-2001
| | Veröffentlicht am Mittwoch, den 26. November, 2003 - 11:17: | 
|
Ja, das ist eine elegante Lösung!
Ich habe gerade gesehen, dass mein Beweis in seiner Form nur für p>1 gilt (ich nehmen an: pk>p). Das ist natürlich dumm.
Könnte man an den Ungleichungen etwas drehen, damit es für alle positiven p gilt?
MfG
Martin
________
Die Natur spricht die Sprache der Mathematik:
Die Buchstaben dieser Sprache sind Dreiecke, Kreise und andere mathematische Figuren.
Galileo Galilei
|