| Autor |
Beitrag |
    
Mausi

Unregistrierter Gast
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 11:02: | 
|
Die 1ste Aufgabe lautet:
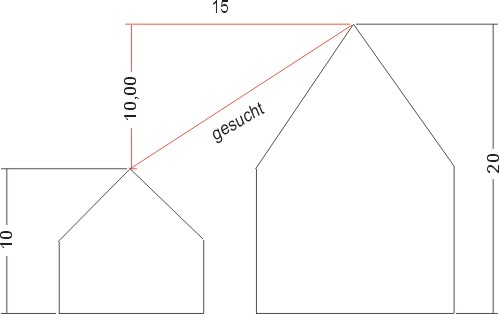
Zwischen den Giebelspitzen zweier Häuser(h1=20m;h2=10m)die 15m voneinander entfernt stehen,soll eine Antenne gespannt werden.
Wie lang muß sie mindestens sein?
und hier die 2te:
Ein Fesselballon ist an einem 300m langen senkrecht stehenden Seil befestigt.
Durch starken Wind wird er 50 m weit abgetrieben .
Wie hoch steht er jetzt über der Ebene?
Wäre echt nett wenn jemand das erklären könnte wenn es geht mit Planfigur.
Bitte!!!
Ich danke euch |
    
Martin (martin243)

Senior Mitglied
Benutzername: martin243
Nummer des Beitrags: 616
Registriert: 02-2001
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 12:24: | 
|
Hi Mausi!
1. Aufgabe:
+++ jpeg +++ 75075 +++ Giebel +++
Wie man der Zeichnung entnehmen kann, beträgt der Höhenunterschied 10 m. Das soll die Kathete a sein.
Die Entfernung soll die Kathete b sein: b=15.
Die Hypotenuse ist dann die Länge der Antenne:
c² = a² + b²
c² = 10² + 15² = 100 + 225 = 325
c = Wurzel(325) = ca. 18 m
(Beitrag nachträglich am 06., Mai. 2002 von martin243 editiert) |
    
Martin (martin243)

Senior Mitglied
Benutzername: martin243
Nummer des Beitrags: 617
Registriert: 02-2001
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 12:27: | 
|
Mist! Hier die Zeichnung:
 |
    
Martin (martin243)

Senior Mitglied
Benutzername: martin243
Nummer des Beitrags: 618
Registriert: 02-2001
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 12:37: | 
|
2. Aufgabe:
Zeichnung:
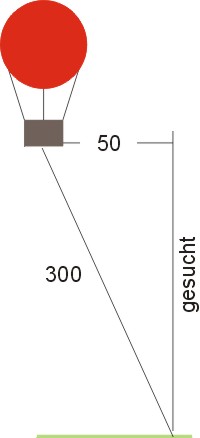
Hier ist die senkrechte Kathete b gesucht.
Die andere Kathete ist: a = 50
Die Hypothenuse wird vom Seil gebildet: c=300.
c² = a² + b²
b² = c² - a²
b² = 300² - 50² = 90000 - 2500 = 87500
b = Wurzel(87500) = ca. 295,8 m
Der Ballon befindet sich also ca. 295,8 m über der Erde. |
    
Mausi

Unregistrierter Gast
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 13:07: | 
|
Hi Martin!
Vielen Dank für die beiden Aufgaben.
Ich habe aber eine Frage:
Wieso ist den die Senkrechte gesucht und nicht in der oberen Zeichnung dargestellte Seite b.
Ich dachte nämlich das die senkrechte Seite gegeben ist.
Mausi |
    
Martin (martin243)

Senior Mitglied
Benutzername: martin243
Nummer des Beitrags: 620
Registriert: 02-2001
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 13:48: | 
|
Ja, es ist zwar am Anfang die Senkrechte.
Aber der Ballon treibt ja ab, was bedeutet, dass das Seil, an dem er hängt, seinen Winkel ändert, aber die Länge gleich bleibt (300 Meter).
Außerdem: Was sollte man dann für eine Höhe suchen, wenn sie schon angegeben wäre?
Noch etwas:
Angenommen, der Wind wird zum Orkan, also sehr stark. Das 300m lange Seil hält dem stand, der Luftballon kann also höchstens 300m abtreiben (Anfangshöhe). Wie hoch wäre er dann? Er würde direkt auf dem Boden liegen, also wäre die Höhe 0m. Auch das ist die senkrechte Höhe, aber unter anderen Bedingungen.
Ich hoffe, es wurde etwas klarer.
Martin |
    
Mausi

Unregistrierter Gast
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 18:25: | 
|
Ja ich denke schon. Wurde nur verwirrt, weil der Ballon ja später nur noch 295,8 m uber der Erde war ,aber auf der Zeichnung genauso hoch steht wie wenn kein wind kommt.
Vielen Dank.
Mausi
|
    
Martin (martin243)

Senior Mitglied
Benutzername: martin243
Nummer des Beitrags: 621
Registriert: 02-2001
| | Veröffentlicht am Montag, den 06. Mai, 2002 - 18:57: | 
|
Nee, Er steht ja auch in der Zeichnung tiefer. Die 300m stehen für die Seillänge, und da das Seil nicht senkrecht nach oben geht, ist die Höhe dementsprechend kleiner als die Seillänge. |
    
kerstin

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 30. Juni, 2002 - 13:05: | 
|
könnt ihr mir helfen ?? der punkt A (3/5) liegt auf dem kreis um M(4/3) . Welche entfernung e hat der punkt B (1/2,5) von diesem kreis ??? ich bräuchte des ergebnis noch heute wenn es geht..
thx kerstin |
    
DULL (dull)

Mitglied
Benutzername: dull
Nummer des Beitrags: 11
Registriert: 06-2002
| | Veröffentlicht am Sonntag, den 30. Juni, 2002 - 15:05: | 
|
Hi Kerstin,
du musst zuerst den Abstand von M und A berechnen. Dieser ist der Radius (r) des Kreises. Nach dem Satz des Pythagoras gilt:
r= Wurzel((4-3)2+(3-5)2)=Wurzel(5)
Nun berechnest du den Abstand d zwischen B und M (also die Entfernung von B zum Mittelpunkt des Kreises):
d=Wurzel((4-1)2+(3-2,5)2)=Wurzel(9,25)
Der Abstand vom Kreis zum Punkt B ist also d-r=0,805313287
Ich hofef ich konnte dir helfen... |