| Autor |
Beitrag |
    
tanja

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 17. April, 2002 - 15:36: | 
|
Hab überhaupt keinen Plan wie man an so iene Aufgabe ran geht ... HILFE bitte!
Gesucht ist eine allgemeine Stammfunktion Fa von fa=(a^2)x-e^(ax).
Welche Stammfunktion von f1 (f1=x-e^x) geht durch den Punkt P(0/1)? |
    
Christian Schmidt (christian_s)

Erfahrenes Mitglied
Benutzername: christian_s
Nummer des Beitrags: 161
Registriert: 02-2002
| | Veröffentlicht am Mittwoch, den 17. April, 2002 - 16:22: | 
|
Hi tanja
ò(a^2)x-e^(ax)dx=1/2*a^2*x^2-1/a*e^(ax)+C
Du bildest die Stammfunktion wie sonst auch immer. Das a ist keine Integrationsvariable, also rechnest du mit a wie mit einer ganz normalen Zahl.
Jetzt zu f1.
F1(x)=1/2*x^2-e^x+C
1=1/2*0-e^0+C
C=2
Also geht die Stammfunktion 1/2*x^2-e^x+2 durch den Punkt P(0|1).
MfG
C. Schmidt |
    
tanja

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 18. April, 2002 - 14:55: | 
|
vielen dank jetz hab ich's verstanden!
dann noch ne Frage dazu
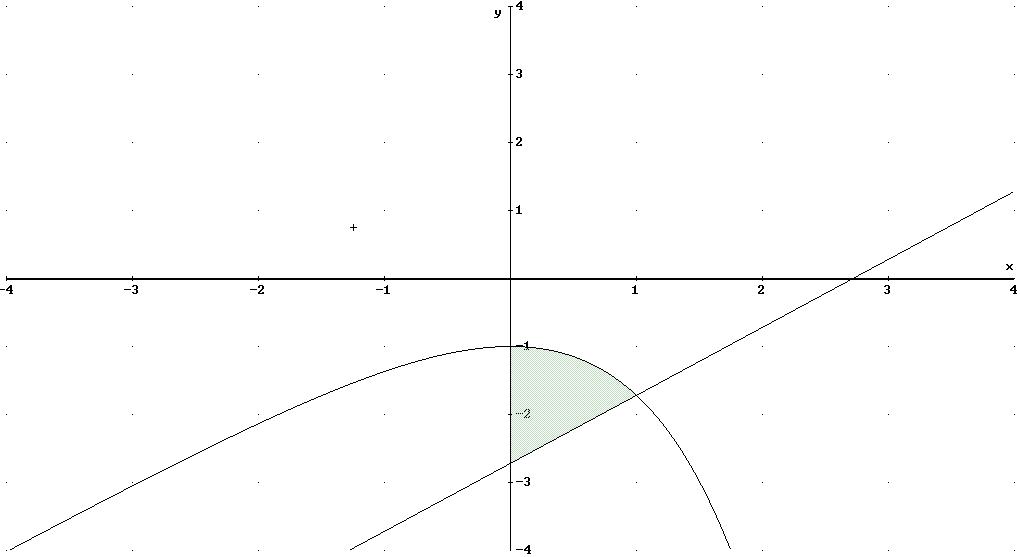
Wenn man jetzt den Inhalt der Fläche, die im 4. Quadranten zwischen dem Graphen von fa (mit fa=(a^2)x-e^(ax)) , der Geraden ga mit ga= (a^2)x-e und der y-Achse liegt bestimmen will ... wie macht man das? Ich blick da nicht durch! Das sind doch 3 Funktionen die die Fläche begrenzen, oder?! |
    
Peter

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 18. April, 2002 - 15:51: | 
|
Die y-Achse ist keine Funktion!
Siehe Skizze
Du musst also von 0 bis zum Schnittpunkt integrieren
 |