| Autor |
Beitrag |
    
Tina

Unregistrierter Gast
| | Veröffentlicht am Montag, den 08. April, 2002 - 20:47: | 
|
hi ihr!
Ich hoffe ihr könnt mir bei ein paar Aufgaben helfen bei denen ich nicht weiter komme!
Das sind Aufgaben für die ich eine gute Zensur bekommen kann die ich dringend nötig habe also bitte helft mir!
f(x)= x³+x²+4/ 2x² ;x ungleich 0
1) Untersuche , ob es eine Parabel g mit g(x)=ax²+bx+c gibt, die den Graph von f sowohl in N(-2 und 0) als auch in (2 und 2) berührt!
2) Für jedes t > 1/2 schneidet die Gerade y=1/2x + t den Graph von f in zwei Punkten Pt und Qt.
Berechne die Koordinaten von Pt und Qt!
Zeige, dass die y-achse jedes Dreieck OPtQt in zwei flächengleiche Teilstücke zerlegt!
Wie groß ist der Flächeninhalt eines solchen Teilstücks? |
    
ugrohne

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 10. April, 2002 - 12:04: | 
|
1.) Für die Berührpunkte kannst Du insgesamt 4 Bedingungen aufstellen, also mehr als ausreichend für die 3 Variablen a,b,c.
Und zwar müssen die beiden Punkte erstmal in beiden Kurven zu finden sein:
f(-2)=0=g(-2) und f(2)=2=g(2)
Du überprüfst erstmal die erste Hälfte der Gleichungen: Du stellst fest, dass die 2 Punkte auch Punkte von f sind, also ist das mal geklärt.
Jetzt gehts ans Aufstellen eines LGS:
Die anderen beiden Bedingungen betreffen das Berühren (sonst wärs ja einfach*g*), in beiden Punkten müssen beide Kurven die gleichen Steigung haben, also brauchst Du die Ableitungen:
f'(x)=1/2-4/x²
g'(x)=2ax+b
Dann bekommst Du die 4 Gleichungen des LGS:
g(-2)=0 und g(2)=0 und g'(-2)=5/2 (-->f'(-2)) und g'(2)=-1/2 (-->f'(2)), also
4a-2b+c=0
4a+2b+c=0
-4a+ b =5/2
4a+ b =-1/2
Aus den letzten beiden Bedingungen kann man a und b bestimmen (a=-3/8 und b=1), und setzt sie in beide vorherigen Gleichungen ein, um sie zu verifizieren: Leider kommt für c nicht das gleiche raus, also gibts eine solche Parabel nicht. Sieht man aber schon am Anfang, da wir dieselbe Gleichung haben oben nur eben einmal ein anderes Rechenzeichen. Damit dann beide Gleichungen stimmen, müsste b=0 sein, das ist aber aufgrund der folgenden Gleichungen nicht möglich.
Ich hoffe, das war ausführlich genug, und das ich keine Rechen-/Denkfehler gemacht habe. Ich versuch mich jetzt noch an der 2.)
Gruß, Uwe |
    
Ingo (ingo)

Moderator
Benutzername: ingo
Nummer des Beitrags: 38
Registriert: 08-1999
| | Veröffentlicht am Donnerstag, den 11. April, 2002 - 13:31: | 
|
Vom Prinzip her hat Uwe die Aufgabe richtig vorgerechnet, leider hat er sich bei der Ableitung von f vertan, so daß sein Ergebnis falsch ist.
Es ist f'(x)=(1/2)-4/x³ was zu folgenden Bestimmungsgleichungen führt
(A) 4a-2b+c=0
(B) 4a+2b+c=2
(C) -4a+b = 1
(D) 4a+b = 0
Dieses System ist eindeutig lösbar mit der Lösung a=-(1/8) b=(1/2) c=3/2
Zur Verdeutlichung noch einmal die beiden Funktionen in einer Graphik
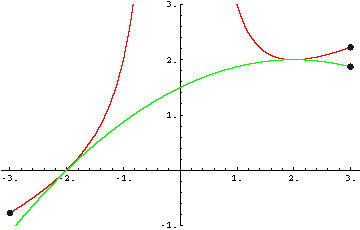
(Beitrag nachträglich am 11., April. 2002 von ingo editiert) |
|