| Autor |
Beitrag |
    
anonym

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 10. März, 2002 - 03:48: | 
|
Hallo,
ich hab da ne kleine Schwierigkeit mit der Aufgabe: Aus einem Zylinder wird ein Kegel herausgeschnitten, das Volumen des "Restkörpers" ist bekannt. Die Höhe h soll nun gerade r betragen. Wie hoch muss ein zu einer kugel vom Radius r gehöriger Kugelabschnitt sein, damit er das gleiche Volumen besitzt???
Ich hab keine Ahnung wie die entsprechende Formel aussehen müsste, wenn jemand ne Idee hat... |
    
A.K.

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 10. März, 2002 - 09:13: | 
|
Hallo Anonym
ich glaub in der Aufgabenstellung fehlt etwas.
Sind z.B. die Radien von Zylinder und Kegel gleich?
Gib doch mal die genaue Aufgabenstellung an.
Mfg K. |
    
anonym

Unregistrierter Gast
| | Veröffentlicht am Sonntag, den 10. März, 2002 - 14:41: | 
|
Hallo K.
die Radien vom Zylinder und Kegel sind gleich gross und der Zylinder ist auch genauso hoch wie der Kegel.
Gruss D. |
    
A.K.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 11. März, 2002 - 09:20: | 
|
Hallo Anonym
warum gibst du nicht die genaue Aufgabenstellung an?
Bisher ist bekannt:
Höhe Zylinder = Höhe Kegel
Radius Zylinder = Radius Kegel
Dann steht in der Aufgabe
das Volumen des "Restkörpers" ist bekannt
Ja, wie groß denn?
Dann folgt:
Die Höhe h soll nun gerade r betragen
Heißt das
Höhe zylinder=Höhe Kegel=Radius Zylinder=Radius Kegel?
Mfg K. |
    
anonym

Unregistrierter Gast
| | Veröffentlicht am Montag, den 11. März, 2002 - 16:25: | 
|
Hallo K.
Bei der Aufgabe geht es um eine hypothetische Lösung nicht um ein konkretes Zahlenbeispiel.
Das Volumen des "Restkörpers" ergibt sich aus der Subtraktion des Volumens des Kegels von dem des Zylinders.
Die exakte Aufgabenstellung für die zweite Aufgabe sieht so aus: "Die Höhe h betrage nunmehr gerade r. Wie hoch muss ein zu einer Kugel vom Radius r gehöriger Kugelabschnitt sein, damit er den gleichen Rauminhalt besitzt?"
Ich weiss nicht so genau was ich mit der Aufgabe anfangen soll...
Gruss Dany
PS. Ich habe den "Namen" anonym deswegen gewält weil mein regulärer Benutzername samt Passwort nicht mehr funktioniert.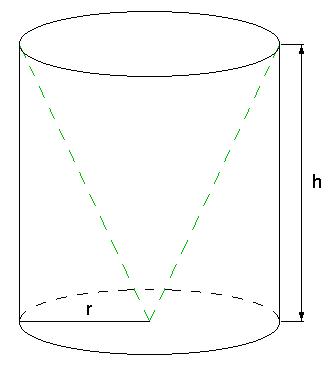 |
    
A.K.

Unregistrierter Gast
| | Veröffentlicht am Montag, den 11. März, 2002 - 21:00: | 
|
Hallo Dany
also nun doch h=r und damit
Restkörper=pi*r²*r-(1/3)pi*r²*r=(2/3)pi*r³
Für das Volumen eines Kugelabschnitts mit dem Radius r gilt
V=(1/3)pi*h²(3r-h)=(2/3)pi*r³ |*3
<=> pi*h²(3r-h)=2pi*r³ |:pi
<=> h²(3r-h)=2r³
<=> 3h²r-h³=2r³
<=> h³-3rh²+2r³=0
<=> (h-r)(h²-2rh-2r²)=0
=> h=r oder h²-2rh-2r²=0
=> h1,2=r±wurzel(r²+2r²)=r±wurzel(3r²)
=> h=r+rwurzel(3)
Mfg K. |
    
Leonie 1988

Unregistrierter Gast
| | Veröffentlicht am Donnerstag, den 05. Januar, 2012 - 14:51: | 
|
Hey .. setze gerade auch vor der Aufgabe .. kannst du mir deine schritte mal schritt für schritt erklären ? .. ^wieso machst du da denn aus einem minus h^3 ein plus .. dann hast du ja einen kompletten vorzeichenwechsel .. -.- |