| Autor |
Beitrag |
    
hey

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 21:32: | 
|
Das ist die stammfunktion:
F(x)=xln(5-x^2)-5^1/2ln[(x-5^1/2)/(x+5^1/2)]-2x
zu berechnen ist die fläche,
die f(x)=ln(5-x^2)mit der
x-achse und x=-2 und x=2 einschließt.
Im lösungsbuch steht A= 4,91FE
meiner meinung nach ist die aufgabe aber nicht lösbar...
Grund: der definitionsbereich von lnx ist R+!!
setze ich "-2" und "2" in die stammfunktion ein, erhalte ich im zähler: -2 - 5^1/2 <0
ln von einer negativen zahl ist doch nicht möglich.
habe nun geprüft, ob die stammfunktion falsch ist.
hab sie abgeleitet und sie ist richtig!!!
danke |
    
2k2

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 23:06: | 
|
falsch!
das Integral lautet:
òf(x)dx=ln(5-x^2)dx
=x*ln(5-x^2)-2*x+2*sqrt(5)*arctanh(1/5*x*sqrt(5))
und so sieht ln(5-x^2)dx aus:
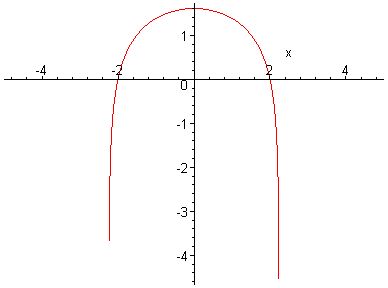
damit dürfte die Aufgabe klar sein!
mfg
2k2 |
    
2k2

| | Veröffentlicht am Montag, den 04. Februar, 2002 - 23:07: | 
|
ein dx war zuviel! |
    
hey

| | Veröffentlicht am Dienstag, den 05. Februar, 2002 - 15:15: | 
|
was ist sqrt?? und was arctanh??
wie bist du darauf gekommen, dass die angabe im lösungsbuch falsch ist??
wie hast du die echte stammfkt gefunden?
( einfach mit dem taschenrechner oder anders?)
thanx |
    
2k2

| | Veröffentlicht am Dienstag, den 05. Februar, 2002 - 18:39: | 
|
hi hey,
die Stammfunkiton habe ich aus Zeitmangel mit Maple berechnen lassen.
sqrt() == Wurzel von
arctanh ==Arcus Tangens Hyperbolicus
Da ich immer noch keine Zeit habe das Integral manuell auszurechnen, schlage ich vor die Funktion nochmal unter "Integrale/Stammfunktion"
einzustellen
mfg
2k2 |
    
hey

| | Veröffentlicht am Dienstag, den 05. Februar, 2002 - 19:04: | 
|
blöde frage, aber was ist arcus tanges hyperbolicus?? |
    
Ludewig

Unregistrierter Gast
| | Veröffentlicht am Mittwoch, den 20. März, 2002 - 23:56: | 
|
Das kann ich hier einfach nicht so stehen lassen...
Die Stammfunktion im Lösungsbuch ist natürlich NICHT FALSCH, sondern nur eine andere Darstellung der selben Funktion.
(okay, natürlich ist es nicht, dass Lösungsbücher immer fehlerfrei sind, aber egal...)
Also:
Der Sinus Hypobolicus ist definiert als
sinhx = (e^x-e^(-x))/2
Der Cosinus Hypobolicus ist definiert als
coshx = (e^x+e^(-x))/2
Der Tangens Hypobolicus ist nun
tanhx= sinhx / coshx
oder
tanhx = (e^x - e^(-x))/(e^x + e^(-x)).
Diese Funktionen sind also eigentlich nur neue Namen für Funktionen, die man auch so Hilfe der e-Funktion schreiben könnte. Nur kommen sie in einigen mathematischen und technischen Gebieten häufiger vor. In der Schule werden sie oft nicht durchgenommen, weil man sie -sozusagen- nicht wirklich braucht.
Das gilt nun auch genauso für den ArcusTangensHyperbolicus, der definiert ist als die Umkehrfunktion des TangensHyperbolicus, denn auch diese Umkehrfunktion ist elementar nur mit Logarithmen darstellbar:
y=arctanh(x)
tanhy = x
sinhy/coshy = x
sinhy = x*coshy
(e^y - e^(-y))/2 = x*(e^y + e^(-y))/2
e^y - e^(-y) = x*(e^y + e^(-y)
Beide Seiten mal e^y
e^2y -1 = x(e^2y +1)
e^2y -1 = xe^2y +x
e^2y - xe^2y = 1+x
(1-x)e^2y = 1+x
e^2y = (1+x)/(1-x)
2y = ln[(1+x)/(1-x)]
y= (1/2)*ln[(1+x)/(1-x)]
Deshalb die unterschiedlichen Lösungsformeln.
Die im Lösungsbuch ist in der Logarithmus-Darstellung, Maple liefert dagegen wohl die arctanh-Version, da diese wohl leicht schöner aussieht oder ... ich weiß nicht wieso.
Jedenfalls braucht man diese Hyperbel-Funktionen nicht zum Lösen dieser Aufgabe.
Ich hoffe, ich konnte irgendwie helfen.
Ludewig |
|