| Autor |
Beitrag |
    
Anonym

| | Veröffentlicht am Dienstag, den 08. Februar, 2000 - 20:41: | 
|
Durch einen gegebenen Punkt soll eine Gerade gelegt werden, die von einem gegebenen Winkel ein Dreieck gegebenen Umfangs abschneidet. |
    
Reinhard Gruber

| | Veröffentlicht am Dienstag, den 08. Februar, 2000 - 22:00: | 
|
Hallo!
Habe versucht, deine Aufgabe allgemein durchzurechnen. Spätestens beim zusammenstellen der Formel für den Umfang habe ich festgestellt, daß diese Angabe von dir unmöglich eine Aufgabe sein kann. Da müssen mindestens noch ein paar Angaben dabeigewesen sein. Schau lieber nochmal nach und meld dich nochmal.
Reinhard |
    
Anonym

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 07:13: | 
|
Hallo! Die Aufgabe ist korrekt. |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 12:28: | 
|
Hallo!
Ich muß zugeben, deine Aufgabe macht mir ziemlich zu schaffen. Eines ist mal klar: mit rechnen (man nehme einen allgemeinen Punkt P=(xp,yp)...) kommt man nicht weit, es muß konstruiert werden und da ist der Strahlensatz ein heißer Tip: man zeichne eine beliebige Gerade, meße den Umfang, konstruiere die gesuchte Gerade so, daß das beliebige Dreieck auf das Dreieck mit dem gesuchten Umfang zusammenschrumpft. Das Problem: Sowohl die durch P zu legende Gerade bildet Strahlen und der Winkel besteht auch aus zwei Strahlen, der Satz hingegen ist für Strahlen und Parallele Geraden ausgelegt. Ich habe den ganzen Vormittag herumgetüftelt, bin aber nicht zum Ergebnis gekommen.
Habt ihr in der Schule vielleicht einen speziellen Satz gelernt, mit dessen Hilfe diese Aufgabe zu lösen sein könnte? Oder überhaupt: was habt ihr als letztes im Unterricht gemacht, bevor ihr diese Aufgabe bekommen habt?
Ich weiß sonst wirklich nicht weiter.
Reinhard |
    
Anonym

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 13:37: | 
|
Hallo Reinhard!
Um Mißverständnissen vorzubeugen: Die Aufgabe stammt nicht aus dem üblichen Schulbetrieb. Eher im Gegenteil: Auf dieser site wurde ich mit dem Wunsch nach interessanten Aufgaben begrüßt. Dem möchte ich gelegentlich nachkommen, insbesondere mit "schlichten" Fragen aus der Elementargeometrie. Zirkel, Lineal und Kreativität - mehr nicht. Zur Kennzeichnung vielleicht ein Sternchen vorweg. ;-)
Bei der obigen Frage spielen Tangenabschnitte eine Rolle.
by |
    
habac

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 14:28: | 
|
Danke für den Tip! Jetzt kommt einmal das berühmte kleine s von der H.-F. zum Zug! |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:30: | 
|
f:
 dreieck.jpg dreieck.jpg |
    
habac

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:34: | 
|
Mein s ist ja gar nichts anderes als Dein U/2. |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:35: | 
|
meistens ist das Problem, daß Bilder nicht mitgeschickt wurde, bei mir ist es umgekehrt, da ist der Text ausgeblieben, also hier ist er:
Hey, ich muß sagen, das Beispiel hat es in sich.
Übrigens, Habac, das s brauchst du nicht:
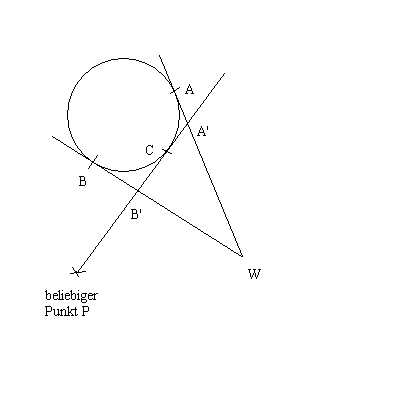
Ich habe zur besseren Vorstellung eine Skize gemacht:
\image{dreieck.jpg}
Schreibt man in den Winkel W einen Kreis ein und zeichnet die Tangente an einen Punkt im dem Winkel nähergelegenen Kreisbogen, so ist der Umfang des so entstandenen Dreiecks konstant, nämlich 2*AW (AW ist die Strecke von A nach W)
Bew: Strecke CA' ist gleich A'A, Strecke B'C ist gleich BB', und WB ist gleich WA, alles wegen Satz über Tangenten (keine Anhnung wie der heißt). Umfang d. Dreieck: WB' + B'A' + A'W =
WB' + B'C + CA' + A'W = wegen oben festgestellten gleichheiten
WB' + B'B + AA' + A'W = WB + AW = 2*AW
Der Winkel ist gegeben, Konstruiere also den Kreis so, daß AW = U/2 (U ist gegebener Umfang) und die gesuchte Gerade durch den gegebenen Punkt P muß den Kreis auf dem dem Winkel nähergelegenen Kreisbogen tangieren.
Der Tip mit der Tangente hat weitergeholfen. Wäre von selber nie draufgekommen. Irgendwie war ich total darauf eingestellt, daß es sich um ein Hausaufgabenproblem handelte. Natürlich freue ich mich über derlei Beispiele, aber hast recht, eine Kennzeichnung würde Mißverständinssen vorbeugen.
Reinhard |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:39: | 
|
Habac, natürlich ist s nichts anderes als U/2, aber wenn man die Variable s nimmt, dann nur im Zusammenhang mit der Heronischen Formel, oder wenn du den Innkreisradius ausrechnest oder ähnlilches, um die Formel abzukürzen. Aber für den einen Satz "in dem Abstand, daß AW = U/2 ist" besteht kein bedarf, abzukürzen
Reinhard |
    
habac

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:42: | 
|
Ich habe das s genommen, weil ich die Lösung nicht verraten wollte, sondern nur ein wenig weiterhelfen. |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:43: | 
|
Habac, natürlich ist s nichts anderes als U/2, aber wenn man die Variable s nimmt, dann nur im Zusammenhang mit der Heronischen Formel, oder wenn du den Innkreisradius ausrechnest oder ähnlilches, um die Formel abzukürzen. Aber für den einen Satz "in dem Abstand, daß AW = U/2 ist" besteht kein bedarf, abzukürzen
Reinhard |
    
reinhard

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 15:46: | 
|
Entschuldige, daß bei mir gerade so ein durcheinander ist, aber mein Windows spielt verrückt (wegen der Sache mit dem Bild und daß die letzte Nachricht 2 mal gesandt wurde) |
    
Anonym

| | Veröffentlicht am Mittwoch, den 09. Februar, 2000 - 22:23: | 
|
Ich freue mich über die Lösung! Die Veröffentlichung der Aufgabe wurde übrigens von Herrn Kolmogorow betrieben. :-) |
    
Susanne Schneevoigt (Sanni15)

| | Veröffentlicht am Sonntag, den 17. September, 2000 - 09:27: | 
|
Hallo,ihr müßt mir helfen !!
In einem gleichschenkligen Dreieck ist die Seite
c=124,8m und der Winkel ß=36°.Es sollen die Seiten
a und b,die Winkel d(alpha)und y(gamma) und der
Flächeninhalt A berechnet werden.Ist das korrekt:
d=ß=36° also d=36° cosß= (c:2):a
a= (c:2):cosß
ß=90°-(y:2) a=62,4m:cos 36°
y:2=90°-ß a=77,13 m
y:2=90°-36° b=77,13m
y:2=54°
y=108° Wie berechnet man den Flächen-
inhalt ?Sind die anderen Berechnungen richtig ?
Bitte helft mir !Sanni |
    
Kai

| | Veröffentlicht am Montag, den 18. September, 2000 - 23:02: | 
|
Die Winkel stimmen, Sanni.
Der Rest auch |
    
Kai

| | Veröffentlicht am Montag, den 18. September, 2000 - 23:08: | 
|
Fläche = a/2 * Höhe.
Höhe mit den Winkelformeln (ähnlich wie oben) berechnen.
Kai |
    
Erwin

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 13:54: | 
|
Ich muss in Mathe gerade ein Arbeitsblatt fertig stellen.Könnt ihr mir dabei helfen?
A) Such eine Zahl, die auf der Zahlengeraden von 1/2doppelt so weit entfernt istwie von -3/4. Wie viel solche Zahlen gibt es?
B)Welche Zahl liegt auf der Zahlengeraden in der Mitte zwischen der Gegenzahl und der Kehrzahl von 2,4?
C)Welche ganzen Zahlen haben:
a) als Betrag eine Primzahl mit der Quersumme 4
b) als Quadrat eine 2stellige, durch 3teilbare Zahl
c)als Kehrzahl ein 3stellige natürliche Zahl mit der Quersumme 4 |
    
doerrby

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 14:43: | 
|
Bitte demnächst neuen Beitrag anfangen!
A) Die gesuchte Zahl sei x. Es soll gelten: |x - ½| = 2 * |x - (-3/4)|
Zum Auflösen der Betragsstriche gibt es die Möglichkeiten
1) x<-3/4: -x+1/2 = 2 * (-x + (-3/4)) | + 2x - 1/2
x = 2 * (-3/4) - 1/2 = -2
2) -3/4£x£1/2: -x+1/2 = 2 * (x - (-3/4)) | -2x -1/2
-3x = 2 * 3/4 -1/2 = 1
x = -1/3
3) x>1/2: x - 1/2 = 2 * (x + 3/4) | -2x +1/2
-x = 2 * 3/4 + 1/2 = 2
x = -2 ( liegt nicht im vorgegebenen Bereich, siehe 1) )
B) Gegenzahl heißt vermutlich hier -2,4 und Kehrzahl 1/2,4 = 0,4167
Die Mitte erhält man, indem man die beiden Zahlen zusammenzählt und durch 2 teilt:
1/2 * (-2,4 + 1/2,4) = -0,9917 = -119/120
C)
a) ±13 , ±31 , ±103 , ±211 , ... Da gibt's noch viele mehr, das waren sie bis 1000.
b) 6 , 9
c) Die Kehrzahlen von 103 , 112 , 121 , 130 , 202 , 211 , 220 , 301 , 310 , 400
Gruß Dörrby |
    
Erwin

| | Veröffentlicht am Sonntag, den 21. Januar, 2001 - 16:59: | 
|
Hallo Dörrby !
Ganz ganz vielen Dank für die Hilfe. Ich muß mir das jetzt erstmal angucken ... so viele Zahlen.
Also danke nochmal. bis dann GRUSS Erwin |
|