| Autor |
Beitrag |
    
Stefan

| | Veröffentlicht am Freitag, den 27. April, 2001 - 16:16: | 
|
Gegeben ist ein Quadrat Q mit der Seitenlänge 2cm. Konstruiere ein Quadrat, dessen Flächeninhalt 3mal so groß ist wie der von Q.
Darf man dort dieses ausrechnen?
2*3=6
6²-2²=x²
Und dann danach das nächste Quadrat ranzeichnen, um ein rechtwinkliges Dreieck zu erhalten, dessen Hypotenuse dann 6cm lang ist??
Oder muss man das ganz konstruieren? Wenn ja, wie macht man das???
In einer Turnhalle hängt ein Kletterseil so, dass noch 50cm dieses Seils auf dem Boden liegen. Zieht man das untere Seilende 2,5m zur Seite, so berührt es gerade noch den Boden. Wie lang ist das Seil? Fertige eine Skizze an.
Danke schon mal! |
    
Raz (Raz)

| | Veröffentlicht am Freitag, den 27. April, 2001 - 16:43: | 
|
Hier geht es nicht um die 3fache Seitenlänge, sondern um den 3fachen Flächeninhalt. D. h. du mußt rechnen:
22 cm = 4 cm2
4cm2 * 3 = 12 cm2
Wurzel 12 cm2 = ca. 3,46 cm
Wie du die nächsten Aussagen meinst, habe ich nicht ganz verstanden. Was für ein Dreieck meinst du? Wenn das jemand anderes verstanden hat, mag er es gerne einbringen.
Was willst du konstruieren?
2) Hier hat man einfach ein Dreieck (wenn ich die Aufgabe richtig verstanden habe). Die eine Kathete sollte x + 50 cm sein, die andere ist 2,5 m.
Versuch mal selbst, ob du damit auf eine Lösung kommst.
Ralph |
    
Zorro

| | Veröffentlicht am Freitag, den 27. April, 2001 - 20:47: | 
|
Hi Stefan,
zur 1. Aufgabe
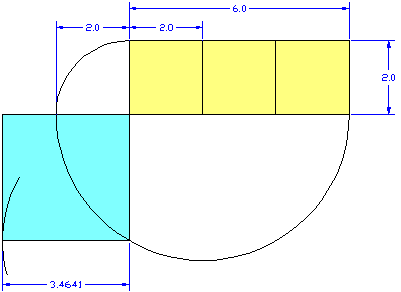
Diese Aufgabe kann man auch völlig ohne Rechnung lösen:

- An das vorgegebene Quadrat werden zwei weitere, identische Quadrate ergänzt.
- Man erhält ein Rechteck mit dem 3-fachen Flächeninhalt des vorgebenen Quadrats
- Aus dem Rechteck wird ein flächengleiches Quadrat konstruiert
- Dazu bevorzuge ich den Höhensatz h² = p*q
- d.h. mit Thaleskreis ein rechtwinkliges Dreieck konstruieren mit p=2; q=6.
- Die Höhe dieses rechtwinkligen Dreiecks ist die gesuchte Seitenlänge des Quadrates.
zur 2. Aufgabe
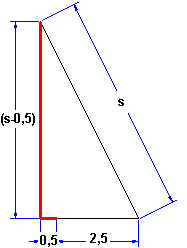
Ich nehme zunächst als Voraussetzung an, daß das Seilende in die gleiche Richtung gezogen wird, in der es zu Beginn auf dem Boden lag.
Dann kann man folgendes rechtwinkliges Dreieck aufstellen:

s² = (s-0,5m)² + (2,5m+0,5m)²
s² = s² - s*1m + 0,25m² + 9m²
s = 9,25m
Das Seil ist 9,25m lang.
Gruß, Zorro |
    
Zorro

| | Veröffentlicht am Freitag, den 27. April, 2001 - 20:52: | 
|
Nanu, das hat wohl nicht geklappt...
Hier nochmal die Bildchen
 |
    
Stefan

| | Veröffentlicht am Samstag, den 28. April, 2001 - 10:37: | 
|
Vielen Dank! Ich drucke das gleich aus! |
|