| Autor |
Beitrag |
    
FAbi (Rainbow)

| | Veröffentlicht am Sonntag, den 01. April, 2001 - 12:02: | 
|
HI
Der Wettbewerb ist vorbei also don't panic! Ich hätte die Lösung eher zum Training für die 4.Runde in Magdeburg.
Beweise: Verbindet man in einer dreiseitigen Pyramide die Mittelpunkte zueinander windschiefer Kanten, so schneiden sich die drei Strecken in einem Punkt. |
    
kelly

| | Veröffentlicht am Montag, den 02. April, 2001 - 15:58: | 
|
Was für ein Wettbewerb ist das? |
    
anonym

| | Veröffentlicht am Montag, den 02. April, 2001 - 20:14: | 
|
Ich denk das gilt für allgemeine Pyramide?! |
    
FAbi (Rainbow)

| | Veröffentlicht am Montag, den 02. April, 2001 - 20:18: | 
|
kelly: Nennt sich "Mathematik-Olympiade". Die Aufgabe ist aus der dritten (Landes-) Runde, welche bereits abgeschlossen ist und ich will zum üben die Lösung :-)
anonym: Jepp, ist in jeder allg. dreiseitigen Pyramide so... Beweise!!!
:-) |
    
philipp

| | Veröffentlicht am Dienstag, den 03. April, 2001 - 19:22: | 
|
Vielleicht hilft dies auch schon weiter:

Ich muss dir ja sicher nicht beweisen, dass Dreieck ABC und A'B'C' ähnlich sind, oder?
Ich würd sagen deshalb gehen AA' und BB' und CC' durch das gemeinsame Zentrum. |
    
philipp

| | Veröffentlicht am Dienstag, den 03. April, 2001 - 19:24: | 
|
Vielleicht hilft dies auch schon weiter:
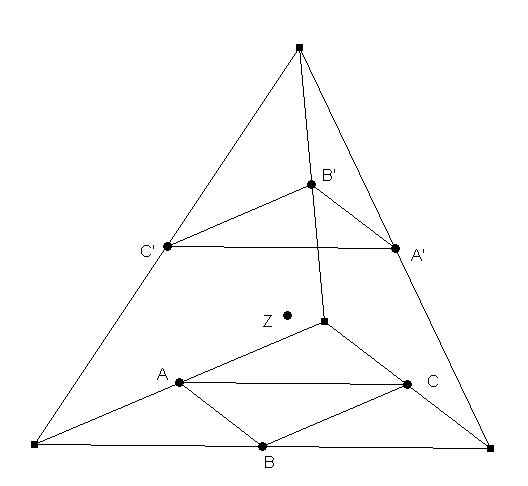
Ich muss dir ja sicher nicht beweisen, dass Dreieck ABC und A'B'C' kongruent sind, oder?
Ich würd sagen deshalb gehen AA' und BB' und CC' durch das gemeinsame Zentrum. Wenn vielleicht nicht ganz vollständig, so zumindest ein Anfang |
|