| Autor |
Beitrag |
    
Bom (Bom)

| | Veröffentlicht am Freitag, den 30. März, 2001 - 15:29: | 
|
Hi!
Folgende Aufgabe: Berechne die Strecke MP im unten abgebildeten Quader. P ist Seitenmitte von CG und M teilt AE im Verhältnis 1:3. Warum ist mein mit dem Computer in rot eingezecihnet Dreieck MBP nicht rechtwinklig?
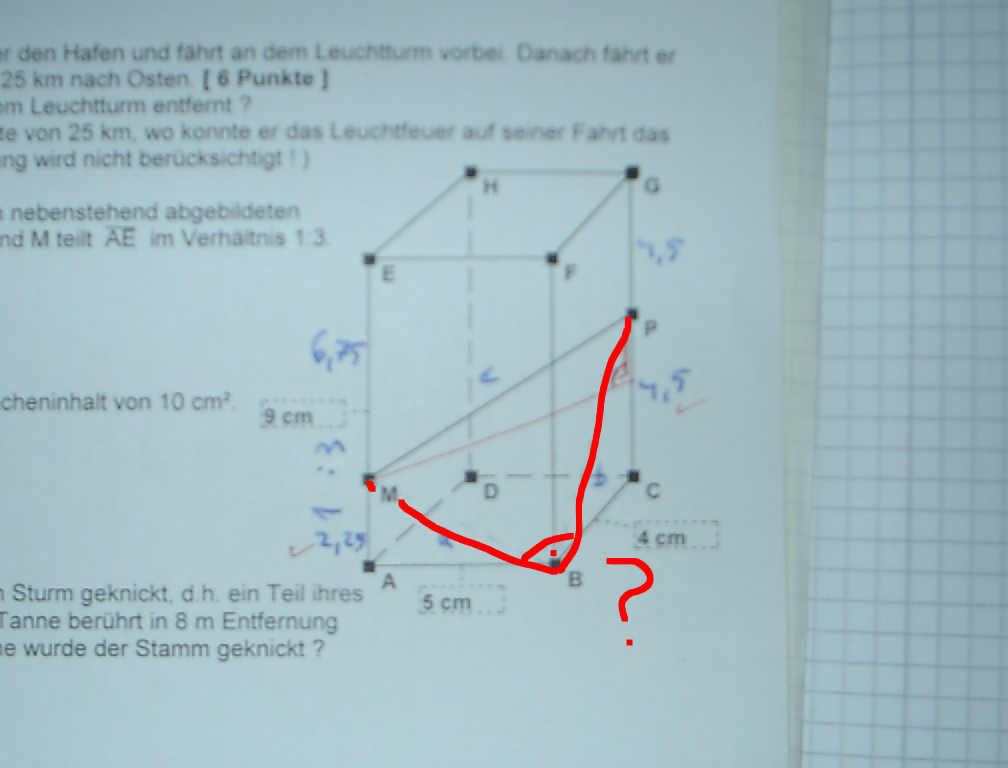 |
    
Sven

| | Veröffentlicht am Freitag, den 30. März, 2001 - 15:59: | 
|
Nu ja, die Seite BP muß rechtwinklig sein. Wenn man ein Viereck entlang der Flächendiagonalen in zwei Teile teilt, entstehen zwei rechtwinklige Dreiecke.
Da aber der Quader schief zum Betrachter steht, scheint es so, als ob es kein rechter Winkel sei. Und ADC ist doch auch nicht rechtwinklig, oder?
Falls du noch die Lösung für die Aufgabe brauchst (sieht ja nich so aus) dann schreib zurück.
MfG und FdH |
    
Sven

| | Veröffentlicht am Freitag, den 30. März, 2001 - 16:00: | 
|
Sorry, es muß "der Winkel MBP" heißen. |
    
doerrby

| | Veröffentlicht am Freitag, den 30. März, 2001 - 16:07: | 
|
Du solltest das Zeug mal ein bisschen kleiner einscannen!
Rechte Winkel hast Du auf jeden Fall, wenn Du parallel zu den Seiten verlaufende Wege beschreitest. Um von der Höhe her von M nach P zu kommen, musst Du von 1/4 der Höhe (Verhältnis 1:3) auf 1/2 der Höhe (Seitenmitte) kommen, also 1/4 * h = 2,25cm parallel zur Höhe. Länge und Breite durchläufst Du ganz, also b=5cm und l=4cm. Nach Pythagoras kommt man dann auf eine Streckenlänge
MP = Wurzel(2,252 + 52 + 42) cm = 6,787cm.
Für die Strecke MB gehst Du 1/4 der Höhe nach unten (also auch 2,25cm) und dann 5cm auf der Breite entlang, macht beim direkten Weg
MB = Wurzel(2,252 + 52) cm = 5,483cm.
Entsprechend berechnest Du BP (1/2 h ; l) und erhältst
BP = Wurzel(2,252 + 42) cm = 4,589cm.
ABER: Wurzel(MB2 + BP2) = 7,15cm ¹ MP, also ist das Dreieck nicht rechtwinklig.
Gruß Dörrby |
    
Sven

| | Veröffentlicht am Freitag, den 30. März, 2001 - 16:44: | 
|
Moment!
Wurzel(MB2 + BP2) muß ungleich MP sein, da das Dreieck MBP quer durch den Raum läuft und schief steht (ich weiß sonst nicht, wie ich das ausdrücken soll). Da kann man den nackigen Pythagoras nicht anwenden, sondern die Formel müßte lauten Wurzel(MB2 + BP2 - Pe2) wobei e der Punkt unterhalb von P sein soll.
Solche Winkel müssen einfach immer rechtwinklig sein. Stellt euch den Quader doch mal von oben betrachtet vor!
MfG und FdH |
    
doerrby

| | Veröffentlicht am Freitag, den 30. März, 2001 - 18:00: | 
|
Es ging doch nur darum, zu zeigen, dass das Dreieck nicht rechtwinklig ist, und wieso soll ich dann nicht den "nackigen Pythagoras" anwenden und das Ganze zum Widerspruch führen?
Frage Dörrby |
    
Bom (Bom)

| | Veröffentlicht am Freitag, den 30. März, 2001 - 20:31: | 
|
Hat man dort nun ein rechten Winkel oder net? Es geht um eine Arbeit, und noch ein paar Punkt.
Hab nämlich MP mit Phytagoras der roten Linie ausgerechnet, indem ich die Diagonalen jeweils berechnet habe, weil man ja MA und CP vorher errechnen kann. |
    
Fern

| | Veröffentlicht am Freitag, den 30. März, 2001 - 21:16: | 
|
Hallo Bom,
Man sieht doch sofort, dass MBP kein rechter Winkel sein kann.
Denk dir den Winkel ABC (= ein rechter) um die Achse AB gedreht, wobei der Punkt C zum Punkt P gleitet: Also ist ABP ein rechter Winkel.
Wenn aber ABP ein rechter Winkel ist, so kann MBP nicht auch ein rechter Winkel sein, weil beide Winkel einen gemeinsamen Schenkel haben!
=========================== |
    
Bom (Bom)

| | Veröffentlicht am Freitag, den 30. März, 2001 - 21:23: | 
|
Und wie soll ich es dann lösen?
Danke erstmal für die Antworten. |
    
Bom (Bom)

| | Veröffentlicht am Freitag, den 30. März, 2001 - 21:41: | 
|
Also für mich ist da immernoch ein rechter Winkel, weil wenn man das mal sich wie Sven meinte von oben anguckt, sieht es sehr danach aus. Es ist doch egal wie die Strecke von der Wand abgeht, oder? sind doch sozusagen zwei Winkel... |
    
Neomaniac

| | Veröffentlicht am Samstag, den 31. März, 2001 - 00:29: | 
|
stell dir doch mal folgendes vor:
ABP ist rechter Winkel, das ist klar!
Jetzt drehst du diesen um BP nach oben, BP bleibt fest. Dann kommt AP aus dem Quader heraus.
--> Die Begründung von oben auf den Quader zu gucken entfällt, dar dadurch eine Richtung wegfällt.
Was willst Du denn berechnen, dann sage ich dir wie:
Gruss Neo |
    
Ich

| | Veröffentlicht am Samstag, den 31. März, 2001 - 00:33: | 
|
Alos:
ABP ist ein rechter Winkel!
Drehen wir diesen um BP nach oben, so kommt AB aus dem Quader heraus. Du kannst dann im Kopf so lange drehen bis ABP und MBP auf einer Ebene liegen. AB und MB haben aber dann nicht die gleiche Richtung, aber den gleichen Punkt B und den gleichen zweiten Schenkel BP also kann nur eins der beiden ein rechtwinkliges Dreieck sein:
-->ABP leider nicht MBP
Was willst Du denn berechnen? |
    
Bom (Bom)

| | Veröffentlicht am Samstag, den 31. März, 2001 - 13:15: | 
|
Die Länge der Strecke MP, ich hab so was um 6,78 raus, mit einer richtigen Methode glaub ich, verrate ich aber (noch) nicht, weil ich sehen möchte ob es vielleicht noch nen anderen Weg gibt. |
    
doerrby

| | Veröffentlicht am Samstag, den 31. März, 2001 - 14:05: | 
|
Das Ergebnis MP = 6,787 cm ist richtig (s.o.).
Nochmal zu dem Dreieck MBP, das nicht rechtwinklig ist: Um der Anschauung ein bisschen auf die Sprünge zu helfen, stell Dir einfach mal das Dreieck EBG vor. Hier ist nur M weiter nach E und P weiter nach G geschoben, aber man sieht direkt, dass EBG im Punkt B nicht rechtwinklig ist. Entsprechend kannst Du Dir vorstellen, dass auch MBP nicht rechtwinklig ist, auch wenn der Winkel im Punkt B größer ist als bei EBG.
Gruß Dörrby |
    
anonym

| | Veröffentlicht am Sonntag, den 01. April, 2001 - 09:16: | 
|
Ich will ja nix sagen, aber alle Längen sind ganz einfach mit Phytagoras auszurechnen, ich weiß nicht wo eigentlich da das Problem ist?? |
|