| Autor |
Beitrag |
    
Bom (Bom)

| | Veröffentlicht am Freitag, den 30. März, 2001 - 15:19: | 
|
Hi!
Aufgabe: (38 kb groß)
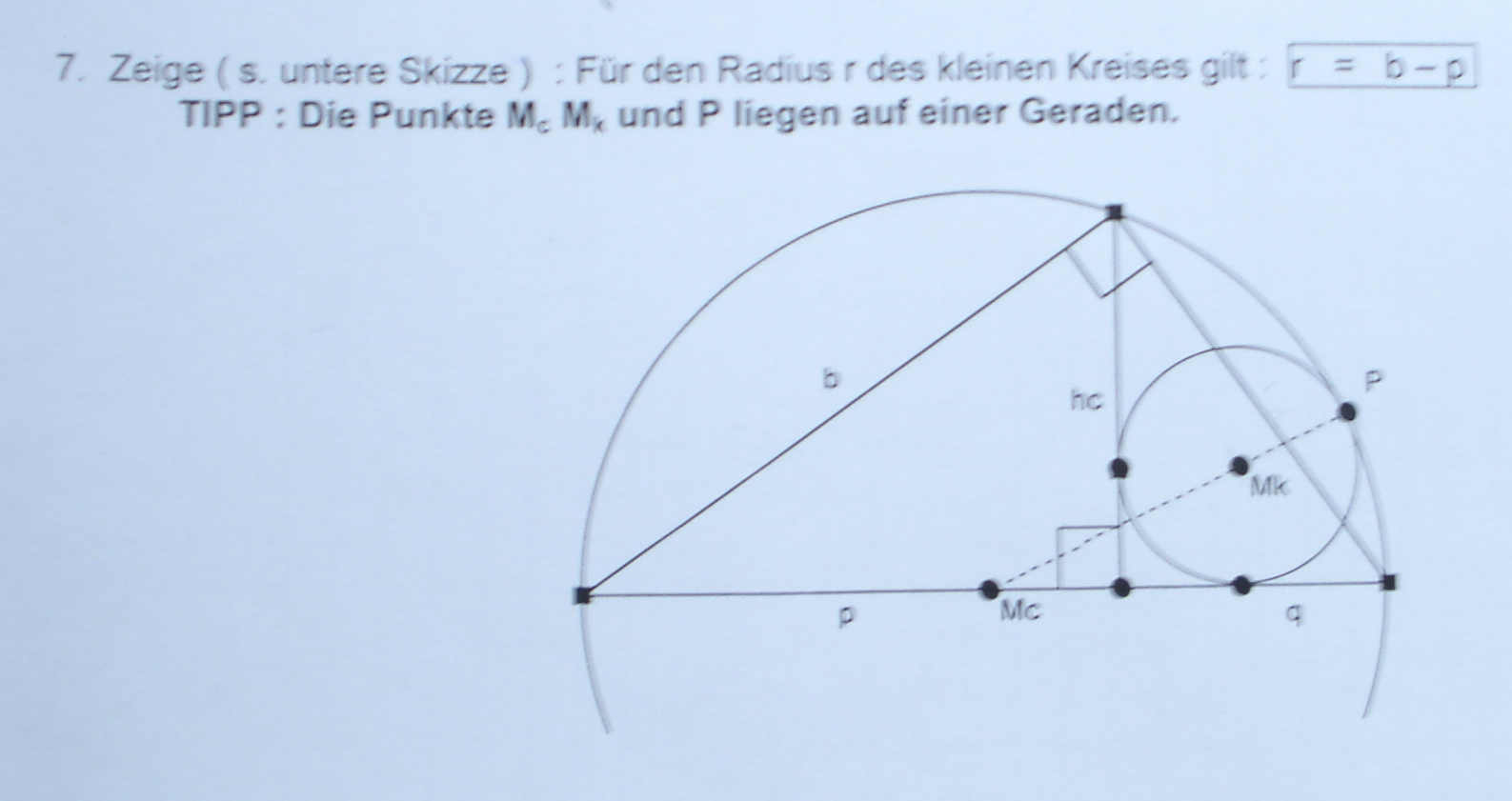 |
    
benutzer

| | Veröffentlicht am Samstag, den 31. März, 2001 - 09:45: | 
|
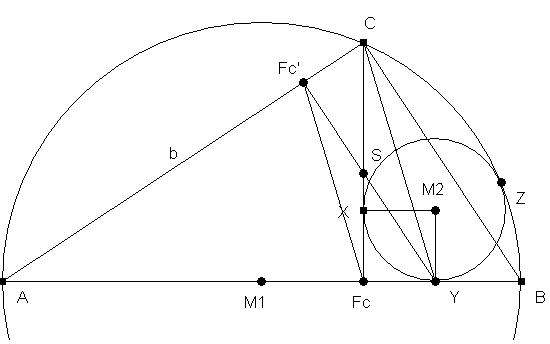
Also ich denk so ist es am einfachsten möglich:
|XM2| = |M2Y| = |M2Z|
<M2YFc {soll Winkel heißen} = 90° // ist der Abstand zu |FcB|
<FcXM2 = 90° //s.o.
=> |FcY| = |XM2| = |M2Y| = |XFc| = r
so jetzt muss man nur noch zeigen, dass b - p = FcY, was ich mit einem gleichschenkligen Dreieck mache:
Dreieck AFcFc' ist gleichschenklig => Dreieck SFcFc' ist ebenfalls gleichschenklig
=> |SFc| = |SFc'|
Das Lot von |AC| durch Fc' schneidet |AB| genau in Y weil :
Dreieck Fc'SC und Dreieck FcYS sind ähnlich (Scheitelwinklel und 90°);
Da auch gilt, dass |SFc| = |SFc'| sind die Dreiecke Fc'SC und FcYS kongruent,
was bedeutet, dass |Fc'C| = |FcY|
Da |Fc'C| = b - p gilt für den Radius des kleinen Kreises: r = b - p |
    
auch-user

| | Veröffentlicht am Samstag, den 31. März, 2001 - 11:16: | 
|
Hallo Benutzer,
Tolles Bild!
Mit welchem Programm hast Du es gemacht? |
    
philipp

| | Veröffentlicht am Samstag, den 31. März, 2001 - 11:53: | 
|
Hallo auch-user
diese Bild ist mit Euklid gemacht worden, tolles Programm für mathematische Konstrucktionen |
    
philipp

| | Veröffentlicht am Samstag, den 31. März, 2001 - 12:02: | 
|
Da fällt mir grad noch ne Variante ein:
{Die Vorarbeit steht noch oben}
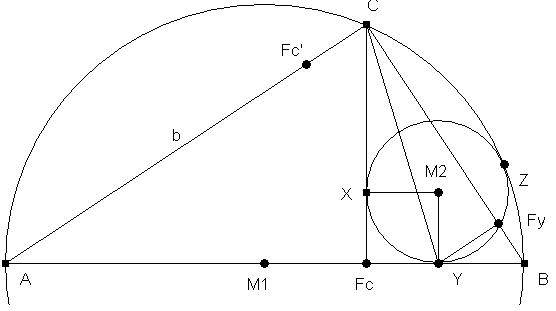
|YFy| ist parallel zu |AC| => <CYFc = <CFyY //Wechselwinkel
=> Dreieck YFyC und Dreieck CYFc sind Kongruent
=> <YCFy = <FcCY = <M2YC = alpha // ich nenne ihn halt mal so
<ACY = 90° - alpha;
<CYA = 90° - alpha;
=> <ACY = <CYA => Dreieck AYC ist Gleichschenklig;
=> AY = AC = b;
=> FcY = b - p;
=> r = b - p; |
    
Bom (Bom)

| | Veröffentlicht am Samstag, den 31. März, 2001 - 13:16: | 
|
Vielen Dank, wo kriegt man dieses tolle Programm her? |
    
Joschi

| | Veröffentlicht am Samstag, den 31. März, 2001 - 13:38: | 
|
Hallo Bom,
Das Programm heißt jetzt GEO.EXE
Gratis download bei
http//www.emath.de
Funktioniert allerdings nur 8 Wochen lang.
Dann Bezahlung von EUR 25,-. |
    
Bom (Bom)

| | Veröffentlicht am Samstag, den 31. März, 2001 - 14:27: | 
|
achso das hab ich schon, aber nich net ausprobiert, werde ich gleich mal machen.... |
    
Bom (Bom)

| | Veröffentlicht am Samstag, den 31. März, 2001 - 20:15: | 
|
Wie zeichnet man den eigentlich diesen Innenkreis? Mit den Winkelhalbierenden geht das ja wohl schlecht. |
    
philipp

| | Veröffentlicht am Sonntag, den 01. April, 2001 - 09:06: | 
|
Welchen Innkreis???
Den einen Kreis hab ich Pi*Daumen gezeichnet, weil ja keine Konstruktionsvorschrift gegeben war. Übrigens, die runden Punkte sind alle konstruiert, d.h. Schnittpunkte von Geraden |
|