| Autor |
Beitrag |
    
Kati

| | Veröffentlicht am Donnerstag, den 21. Oktober, 1999 - 11:32: | 
|
Hi!! Ihr müßt mir Helfen, bitte, bitte, bitte. Ich muß morgen an die Tafel mit der folgenden Übung. Und sie auch erklären können. Also das Ergebnis allein bringt mir nix!!!!!!!!!!!! Bitte ganz lieb guck!!
Gegeben sind die Funktionen f von k durch f von k (x)= x^3-6x^2+9x+k, k element von R
A) Untersuche die Funktionen f von k mit Ausnahme der nullstellenbestimmung ausführlich.
B) Welche Bedingung muß k erfüllen, damit die Funktion f von k genau eine Nullstelle, genau zwei, genau dri Nullstellen besitzt?
c) Ist auch der Fall möglich, daß f von k keine nullstellen besitzt |
    
Pi*Daumen

| | Veröffentlicht am Donnerstag, den 21. Oktober, 1999 - 23:07: | 
|
f(k(x))=x³-6x²+9x+k=x(x-3)²+k=0 <=> x(x-3)²=-k
Die Funktion x(x-3)² geht für x->-¥ gegen x->-¥ und für x->¥ gegen ¥. Da x(x-3)² stetig ist, wird jeder Zwischenwert angenommen und insbesondere auch -k (ist auch aus dem Graphen ersichtlich). Also muß es mindestens eine Nullstelle geben.
Graph:
Die grüne Gerade ist das Beispiel k=-2. Die Schnittpunkte zwischen Gerade und Kurve sind die Nullstellen der Ausgangsfunktion.
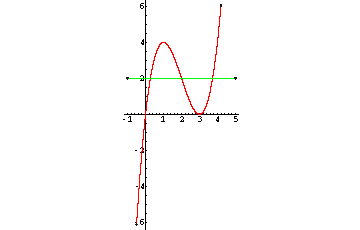
1. Fall: k=0 => x(x-3)²=0 <=> x=0 oder x=3, also genau 2 Nullstellen.
2. Fall : k=-4 => x(x-3)²=4 <=> x=4 oder x=1
3.Fall: -4<k<0: 3 Nullstellen
4.Fall: k<-4 oder k>0: 1 Nullstelle
Sorry, 3. und 4. Fall ist jetzt natürlich noch nicht mathematisch klar bewiesen (wegen der späten Stunde). Aber ich denke, Du hast einen guten Weg, wie es läuft mit der Aufgabe.
Viel Glück!!
Pi*Daumen |
    
Ingo

| | Veröffentlicht am Donnerstag, den 21. Oktober, 1999 - 23:20: | 
|
Ist vermutlich zu spät,aber vielleicht schaust Du Sie Dir morgen früh noch kurz an :
(A)
fk ist als (reelle) Polynomfunktion stetig und beliebig häufig differenzierbar.Keine der Funktionen fk besitzt einfache Symmetrien,da sowohl gerade als auch ungerade Exponenten auftauchen.
Ableitungen :
fk'(x)=3x2-12x+9
fk''(x)=6x-12
Extremstellen liegen dort,wo die Steigung Null beträgt und die 2.Ableitung ungleich 0 ist.
fk'(x)=0 <=> x2-4x+3=0 <=> (x-1)(x-3)=0 => x=1 v x=3
fk''(1)=6-12=-6 -> Maximum im Punkt(1;4+k)
fk''(3)=18-12=6 -> Minimum im Punkt(3;k)
Wendestelle : fk''(x)=0 => x=12/6=2
Als lineare Funktion vollzieht fk'' in der Nullstelle "natürlich" einen Vorzeichenwechsel,so daß der Punkt(2;2+k) tatsächlich einen Wendepunkt der Funktion fk darstellt.
(B) Trickreich : Betrachte das Minimum und das Maximum der Funktion.
a)eine Nullstelle : Maximum und Minimum liegen oberhalb oder unterhalb der x-Achse.
D.h. (4+k>0 und k>0) oder (4+k<0 und k<0)
bzw. k>0 oder k<-4
b)zwei Nullstellen : Minimum oder Maximum liegen auf der x-Achse.
k=-4 oder k=0
c)Drei Nullstellen : Alle übrigen Fälle,also -4<k<0
Um das Vorgehen zu verstehen zeichnest Du am besten eine typische Funktion 3.Grades und verschiebst sie nach oben bzw.unten.
(C) Nein,da eine Funktion 3.Grades immer eine Nullstelle besitzt.Grund : Sie kommt von -¥, geht nach ¥ und ist stetig,also durchgehend.Folglich muß sie irgendwo die x-Achse schneiden. |
    
10d3cs

| | Veröffentlicht am Mittwoch, den 17. November, 1999 - 20:28: | 
|
nabend also:
f(x)=(x^2-4x+3). (x+2) xeR
berechne nullstelle,unendlichkeit,spkte des graphen mit der y -achse,koord der lok extrempkte,art der extrema
berechne die koord der pkte in denen f(x) parallel zur graden g (y=-x+6) ist.
ermittle den flächeninh.der von f(x) und von: P(x)=x^3+6 vollständ. begrenzt wird
geg.ist die funktion h(x)durch y= m.x+6 für welche werte von m besitzen die graphen der fkt. f und h genau 3 gemeinsame pkte?
thanx und ist ziemlich sehr dringend!! |
    
Anonym

| | Veröffentlicht am Mittwoch, den 17. November, 1999 - 20:31: | 
|
ups das war ja gar nicht mein benutzername......*g* |
    
Cori

| | Veröffentlicht am Donnerstag, den 18. November, 1999 - 17:24: | 
|
Untersuche die gegenseitige Lage der Ebenen E1 und
E2. Bestimme eine Parameterdarstellung der Schnittgeraden, falls E1 und E2 sich schneiden.
Folgende Aufgabe dazu:
3 1 7
E1:x= 4 + r -2 + s 4
7 1 0
E2:x1-3x2-9x3= -70 |
    
Doc

| | Veröffentlicht am Freitag, den 19. November, 1999 - 16:56: | 
|
Also dann fangen wir mal an :
Für E2 schreiben wir E2:x-3y-9z=-70
1. Die E1 in E2 einsetzen
das wäre dann:
(3+r+7s)- 3*(4-2r+4s)- 9*(7+r)= -70
jetzt auflösen und zusammenfassen
-72-2r-5s = -70 |+72
-2r-5s = 2 |+5s
-2r = 5s+2|/-2
r =-2,5s-1
2.
Jetzt r in E1 gleichsetzen
(3) (1) (7)
: (4)+ (-2,5s-1)*(-2) +s(4)
(7) (1) (0)
so noch die Klammer auflösen:
(3) (-2,5) (1) (7)
: (4)+ s*(5) -(-2)+s(4)
(7) (-2,5) (1) (0)
nun noch zusammenfassen
(2) (4,5)
: (6)+ s*(9) = g (in Parameterform)
(6) (-2,5)
Mach die Probe (also setze für s ein Wert ein und überprüfe ob der Punkt dann auf E2 liegt) und dann alles KLAR |
|